考虑浮力射流近区垂向效应影响的二维计算方法

张贝贝，段杰辉，高德申，王作廷

（1.中国水利水电科学研究院，北京 100038；2.北京中水科海利工程技术有限公司，北京 100038；3.山东电力工程咨询院有限公司，山东 济南 250013；4.华能丹东电厂，辽宁 丹东 118300）

1 问题提出

温排水排放后，与受纳水体在沿程和垂向掺混，其温度逐渐下降；且因温排水水温高于受纳水体水温，一定情况下排口附近会形成明显的分层跃层现象。温跃层的准确定义并不统一。一般可以先选定温跃层强度的最低指标值，然后对温度标准层资料求其变化率，即垂向梯度，把温度垂直梯度值大于、等于最低指标值所在深度范围称之为温跃层。温跃层强度最低指标，在浅海区（水深不大于200m）可取0.2℃/m［1］。温排水经排放口出流后，如果分层现象渐为弱化，受纳水体表底温度相差不大，温度垂向分布趋于均匀；在排放口附近，一定条件下受纳水体受温排水影响，表底温度会有明显差别，在垂向会存在温跃层。陈惠泉等［2］通过对浅水渠道中水平温差出流的研究认为：以(FΔ0)cr=c β4/3为标准，其中 c=0.54 ， β=Hh0，H为河道水深值，h0为排水口高度；当排水口密度佛氏数 FΔ0＞(FΔ0)cr时，渠道中不会出现温度分层现象；反之，则会发生温度分层现象。由该判断标准可知，渠道水深值对温排水排放后温度分层与否有重要影响。

对于温排水分布进行数值模拟研究时，一般应当考虑二维、三维数值模型的适用性。平面二维模型因深度平均的缘故，无法反映出现分层结构的温排水的特性，但对热量已充分均化的区域的温度分布能够给出可用的结果。三维模型关注了垂直方向上相关物理量的变化情况，可以用来预报研究温排水近区热水层厚度、温度分层现象等。但三维模型的建立及应用存在工作量大，耗时长的特点；且对于温度空间分布均匀程度已很高的区域，三维模型的使用则显得有些“浪费”。可以认为，当水体中流速及温度的垂向变化并不显著，总体水力热力特性可以用二维数模描述；在流速、温度沿垂向变化明显，呈现出较强的三维分布特性时，就需要考虑用三维数模进行模拟［3］。

温排水注入受纳水体后，在靠近排水口的局部水域中，主要呈现的物理现象是掺混稀释，该区域通常称为近区；近区中水温的降低主要靠紊动掺混，且范围有限，水面散热可以基本忽略。经近区掺混后，温排水逐渐向广大水域扩散，同时向大气散热，该区域称为远区。在实践应用中，二维平面模型被广泛应用于温排水的温升分布计算。如何将温排水排放后的近区与远区计算给予区别，同时又能将两者较好结合是值得关注的问题。通常的做法是利用热水出流的理论模型或实验室中的试验资料确定近区的范围及射流轴线流速衰减过程、射流扩散宽度等，将近区从计算域中隔离出来；远区则采用加大网格尺寸，节省计算工作量，其计算条件由近区计算结构提供［4-5］。值得注意的是，该种所谓的远近结合计算方法，只是在水平维度上对近区和远区给予了区别对待，垂向上近远区掺混特性的不同实际上未能考虑。

2 平面二维模型讨论

二维模型在全计算域深度平均的做法使得对温排水近区计算的考虑仅体现在平面特征上，对排水口近区热水层厚度的存在及变化未能给予考虑。对于发生温度分层的情况，二维模型深度平均的做法，使得近区表面温度偏小的问题更加突出。

如图1所示，某电厂温排水均先排入孤形蓄水池后经西南通道入海，其取排水温差为10.6℃。为观察排口附近水深对受纳水体温升分布的影响，在蓄水的水深值分别定为2m、5m、10m和15m（蓄水池之外区域的地形均相同）的假定下进行了4组比较计算。计算所得温升分布及等温升线包络面积如图1、表1所示。

表1 蓄水池等温升线包络面积 （单位：km2）

由图1及表1可以看到：蓄水池在排入相同量相同温度的温排水后，排水口附近4℃、3℃、2℃、1℃表面温升线的包络面积均与蓄水池水深相关明显；二维模型深度平均的做法是造成这一差别的直接原因。而在离排水口较远的区域，等温升线包络面积则基本相同，如1℃、0.5℃的范围。这是由于，在距离排水口较远的区域，温排水已在垂向上均化所致。综合可得出如下结论：（1）实际加入掺混的水深值对热量尚未混合均匀近区的二维模拟结果影响较大；（2）热量垂向混合均匀后，平面二维模型的结果是可信的。

3 考虑近区射流垂向效应的平面二维方法

3.1 计算模式 从上述平面二维模型的简单计算结果可以看出，如在二维计算中适当考虑排放口近区热水层厚度，将有利于提高近区及整体平面温升预报结果的可信度。基于这样的思想，本文提出了一种考虑近区射流垂向效应影响的平面二维计算方法。

该方法的计算模式示意如图2。假定在排放远区温排水垂向掺混充分，首先确定排放口近区因浮力射流而形成的热水层厚度h和温排水在排放口下游垂向掺混大致均匀的位置A。位置A与排放口间的沿程水体，热水层与上游来流进行沿程掺混稀释作用较明显，可称为混合过渡区。对混合过渡区温排水与河道水体掺混过程的处理，参照σ坐标方式考虑加入掺混的流量沿程随水深变化。计算过程中，该二维模型在向深度平均时，混合过渡区L内的垂向计算水深不再是实际水深，而是热水层相应的沿程掺混厚度；直到到达下游均匀掺混区起始位置A后，深度平均时的水深才为相应点的实际水深。由于热水层掺混厚度由排水口至下游均匀区沿程增大，在此区域内垂向均化后的计算值沿程减小，这就体现了温排水与河道水体掺混、稀释的过渡过程。可以看到，温排水自排水口排出至混合过渡区某处后，河道水体向其掺入的流量与该处距排水口的距离有关。对于垂向掺混基本均匀后，使用平面二维模型对温排水温度分布进行计算是可信的。

图3 浮力射流示意

浮力射流层厚度及浮力射流近区尺度与排放口尺度和排放口密度佛氏数密切相关。上面分析公式表明：对于排放口面积一定的情况，排放速度变化时，则浮射流热水层厚度与近区尺度均随排放速度线性变化；而当相对密度差变化时，浮射流热水层厚度与近区尺度均随相对密度差的0.5次方反比例变化。

如某核电厂温排水排放口附近河道被人为挖深，在131m3/s流量下的水深可达10m，设计条件下排放口附近为较典型的深水浮力射流情况；温排水与受纳水体温差为5℃，排放口流量为1m3/s。此情况为典型的三维问题，宜用专门的浮力射流模型模拟［7-9］。从排放流量考虑，该核电厂排放口体形如为5m×0.5m，据此可以对浮力射流近区特征做出理论的分析。其排放流量为1m3/s，相对密度差按1.1‰计算，计算排放口FΔ为5.5，可得：hmax=1.63m；Xmax=61.6m；Xt=21.4m。

上面结果是在无限静流水域获得的，对于窄长形河道情况的应用，会有一定的差别。

该工况下，排放口密度佛氏数FΔ=5.5，结合前述陈惠泉等对温差出流研究内容可得=0.54×(1 0/0.5)43=29.3；由于，因而排水口附近会出现明显的分层流动现象。显然，若不能采用专门的浮力射流模型来模拟计算，则也应在使用二维平面模型计算时考虑到排放口近区的修正，以使得结果趋于合理。

为验证射流厚度，本文利用三维模型［10］对概化情况进行了模拟。按已有河道地形统计分析，修山水库大坝上游计算段边界概化为宽270m×水深10m×长1000m（其中排水口下游约9000m）河槽。计算时河槽流量131m3/s（断面平均流速约4.8cm/s），采用宽5m×深0.5m排放渠在表层进行1m3/s排放流量（平均排放流速0.4m/s）；温排水与河道水体温差5℃。只估算排口射流近区热水层厚度。在近区，水温的降低主要靠紊动掺混。由于出流的动量通量及浮力射流所产生的紊动掺混作用远大于水面散热作用的影响，故计算时，不考虑表面散势的影响。

三维网络最小尺度为5m×10m×0.25m。排水口前射流近区计算剖面结果如下图4。

图4 排放口剖面温升分布图（图中z向比尺是y向比尺的20倍 单位：℃）

三维概化计算表明，排水口正前贴岸1℃热水厚度约1.6m，离岸掺混后0.2℃最厚处约2.2m，其后0.2℃厚约1.2m。排口浮力射流近区计算厚度与前述理论分析的厚度结果是同量阶的。

3.3 排水口下游均匀掺混区起始位置的确定 排水口掺混厚度修正的平面二维模型预报结果，在排水口附近表层水体及充分掺混后的下游水体中是可信的，但在这两块水体之间的过渡区却较为复杂。主要原因是对近区至下游均匀掺混区的缓慢混合过渡区底部边界进行确定是一个困难的工作，特别是对于横流中的浮力排放，可使用的相关研究资料不多。

对于本算例情况，三维概化计算数据表明排放口下游300m开始河槽底部已经开始出现0.001℃温升值，至500m出现渐为频繁，800m时河槽底全部出现［11］。考虑自排放口下游900～1000m处存在一河道急弯（见图5），在弯道流和河床地形的作用下，弯道水体在垂向掺混剧烈，可以认为热量经排口下游1000m处掺混后已达到均匀。

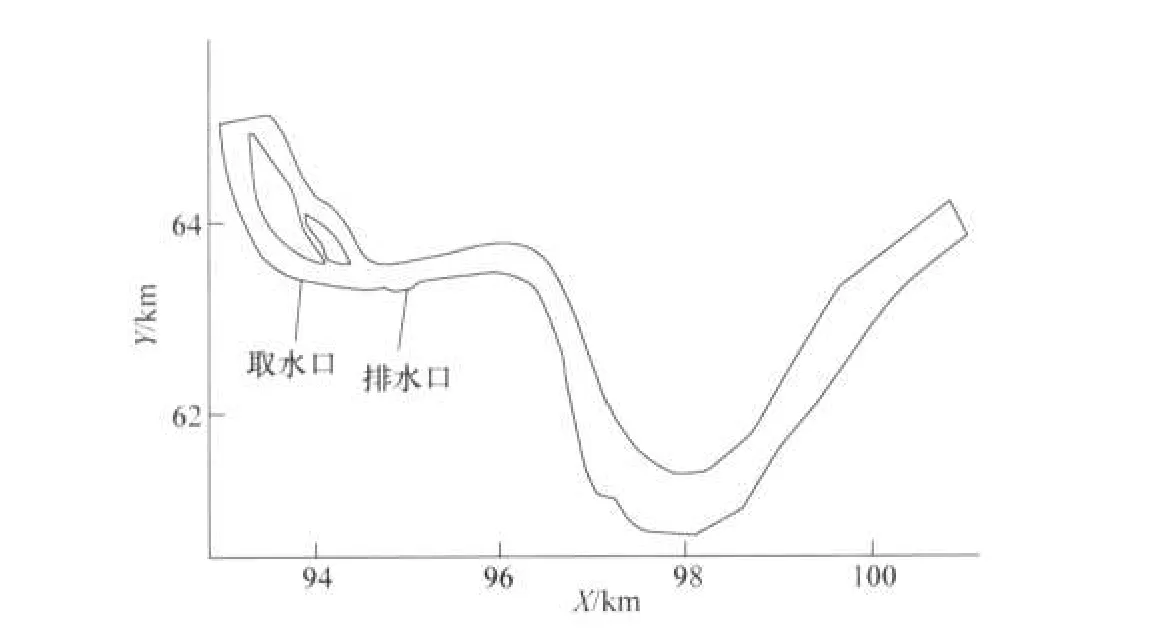
图5 某电厂计算域示意

4 结果比较分析

为比较不同数学模型对温排水近区模拟的异同，在相同的计算条件下，分别应用平面二维模型、考虑近区垂向效应的平面二维计算方法以及三维模型对前述核电厂温排水排放进行了模拟，水体表面温升分布结果如图4、表2、表3。

图6 3种数学模型计算所得温升分布（单位：℃）

表2 等温升线包络面积二维结果 （单位：km2）

表3 表层等温升线包络面积 （单位：km2）

不难看出，由于排水口附近河道水深值较大，平面二维模型将温升值在垂向平均后，近区的1℃温升线已经消失。采用近区修正的平面二维计算方法的结果中，1℃温升线存在于排水口附近。由表2数据可看出：对于0.1℃、0.05℃、0.03℃温升线的包络面积，考虑近区垂向效应的平面二维模型计算结果均大于普通平面二维模型的结果。在三维模型计算条件下，计算域内的温度分布是明显分层的，排放热量只是在水体表层输移。表3表明，对于1℃温升线包络面积，三维模型计算的结果大于考虑近区垂向效应的结果，但在量阶上相同，这与通常的认识是一致的。比较表明，考虑了近区垂向效应的平面二维计算方法，在一定程度上提高了排水口附近表面温升预报的精度，其预报结果较平面二维模型合理。由于近区垂向修正的平面二维计算方法和一般平面二维模型的根本区别在于混合过渡区内参与二维计算的水深值的不同，因此，两者完成相同计算量所耗的机时基本上相同。

5 小结

（1）平面二维模型无法在排水口附近对温排水深水排放时的运动特性进行模拟；深度平均的做法更使得其在受纳水体表面的温升值因排水口附近水深值较大而明显减小；对于排放近区的计算而言，考虑垂向近区效应比考虑平面近区效应更重要。（2）本文提出的在排水口近区利用射流模型进行垂向修正的平面二维计算方法，考虑了温排水热水层厚度以及混合过渡区的变化过程，使得预报的排水口近区表面温升值更趋合理，对于精度要求不是很高的火、核电厂温排放计算具有实用价值。

［1］陈奕德，张韧，蒋国荣，等.太平洋海域温跃层分类及其特征分析［C］//Argo应用研究论文集.北京：海洋出版社，2006：204-214.

［2］陈惠泉，陈燕茹.二元温差出流的局部掺混［C］//水利水电科学研究院文集（第17集）.北京：水利电力出版社，1984：134-135.

［3］李振海，李平衡，吴江航.电厂温排水受纳水域水力热力特性的三维数学模型［R］.北京：中国水利水电科学研究院冷却水研究所，1991.

［4］柳新之，王双.水力热力数学模型的研究（热影响研究的综合分析报告）［R］.北京：中国水利水电科学研究院冷却水研究所，1991.

［5］岳钧堂，杜亚宏，胡素芳，等.辽宁核电站厂址选择冷却水使海域温升的数模计算［R］.北京：中国水利水电科学研究院冷却水研究所，1985.

［6］Hino M，Balkema A A.IAHR 5-Hydraulic structure design manual，water quality and its control［M］.Rotter⁃dam，ISBN 9054101237，1994.

［7］赵振国，文建刚.冷却池的三维异重流计算［J］.水利学报.1992（12）：48-55.

［8］黄柱崇.浅水型冷却池水力热力数学模型的有限元计算［C］//水利水电科学研究院文集（第17集）.北京：水利电力出版社，1984：156-178.

［9］Dunn W E，Policastio A T，Padlock R A.Surface Thermal Plumes：Evaluation of Models for Near and Complete Field［R］.Argonne National Laboratory Report，No.ANL/WR-7517，1975.1.

［10］高德申.分层流温盐横向排放的三维数值模型研究［D］.北京：中国水利水电科学研究院，2009.

［11］段杰辉，张贝贝，高德申.湖南桃花江核电厂AP1000机组温排水数值模拟计算报告［R］.北京：中国水利水电科学研究院，2009.