河道糙率反问题研究回顾与展望

沈五伟，陈一帆，申振东

（1.浙江省水利河口研究院，浙江 杭州 310020；2.浙江广川工程咨询有限公司，浙江 杭州 310020）

河道糙率反问题研究回顾与展望

沈五伟1，2，陈一帆1，2，申振东1，2

（1.浙江省水利河口研究院，浙江 杭州 310020；2.浙江广川工程咨询有限公司，浙江 杭州 310020）

河道糙率是河流水力计算的关键灵敏参数，也是众多因素影响的综合性参数。工程上常用的查表法、公式法和试错法得出的糙率值往往难以满足水力计算要求，因此河道糙率反演理论和方法研究引起了国内外学者的广泛重视。在回顾和总结河道糙率确定基本方法和优化反演方法研究进展的基础上，指出了河道糙率反问题研究面临的困难和挑战，展望了河道糙率反问题研究的发展方向。

河道糙率；反演分析；糙率率定

1 问题的提出

河道糙率，本质上是反映床面岸滩粗糙程度、河道空间不规则性、水流水力状态变化等众多因素对水流运动阻力影响的重要水力参数，是河流水力计算的关键灵敏参数，其取值的合理性直接关系到河流水力计算结果的精确性和可靠性。虽然河道糙率时空变化已有一些经验规律可循，但由于影响河道糙率的因素众多、复杂多变，因此对其进行量测计算相当困难，常采用间接方法进行确定，包括河道糙率确定基本方法和优化反演方法2大类。

针对河道糙率，本文在回顾和总结河道糙率计算研究成果的基础上，提出了河道糙率优化反演方法的评价标准，指出了河道糙率反问题研究面临的困难和挑战，最后展望了河道糙率反问题研究的发展方向。

2 河道糙率确定基本方法

由于天然河流的复杂性，仅依据糙率影响因素对糙率进行定量分析尚不可行。通过长期理论和实践研究，河道糙率确定已有一些经验公式、图表对照或调试演算等基本方法供工程技术人员参考使用。目前，糙率确定的基本方法见表1。

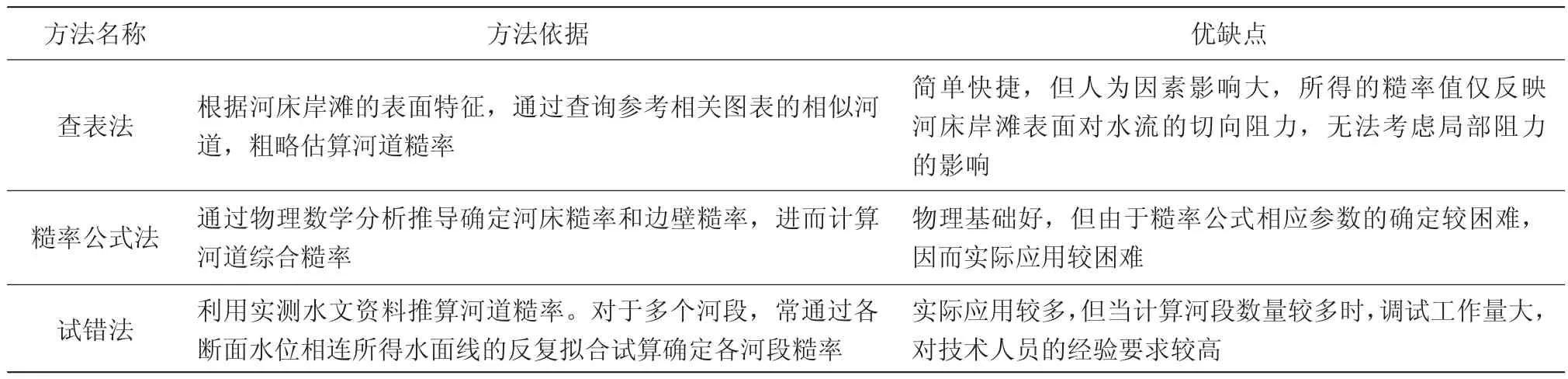
表1 河道糙率确定基本方法表

上述糙率确定基本方法具有较大的盲目性和不确定性，具体表现为：①糙率确定受人为因素影响明显，率定结果往往因人而异，具有一定的随意性；②随着河段数量的增多，糙率确定工作量和率定难度显著增大，对工程技术人员的经验要求随之提高；③由于缺乏系统的理论指导，率定结果的可靠性难以有效评估，结果的准确性得不到合理保障。因此河道糙率反演研究（或称为河道糙率辨识研究）引起了国内外学者的广泛重视。

3 河道糙率确定优化反演方法

3.1 河道糙率优化反演含义

河道糙率优化反演是根据水文测站测得的水位、流量等水力要素观测资料，采用系统优化方法，将河道糙率的率定过程编制成优化反演程序来实现糙率的自动率定，这样既保证了水力要素观测值与模拟值的合理匹配，又可显著降低人工试算的工作量。由于描述一维非恒定明渠水流运动的圣维南方程组是非线性双曲型偏微分方程组，断面糙率和水力要素之间呈现明显的非线性关系，同时由于河道水流是复杂多变的动态系统，因此河道糙率优化反演问题为动态系统非线性反演问题。

3.2 河道糙率优化反演研究现状

Becker等[1]采用结合敏感度分析的单纯形法进行了河道糙率的反演研究；WasanthaLal等[2]建立了基于奇异值分解的河道糙率反演模型，并提出了糙率分辨率的概念；Atanov等[3]采用拉格拉日算子变分法对规则棱柱形河道的糙率进行了反演研究；Khatibi等[4]采用高斯 — 牛顿优化方法进行河道糙率的反演研究，分析了准则函数和样本数量对反演结果的影响；Ramesh R.等[5]建立了基于顺序二次规划算法的河道糙率反演模型，分析了不同噪声水平下反演模型的率定效果；董文军等[6]利用Frechet微分概念和构造相应的协态方程来确定目标函数的下降方向，并用牛顿一辛普森迭代法求解糙率优化反演模型；李光炽等[7]较先探索采用卡尔曼滤波进行河道糙率反问题的研究；程伟平等[8]基于广义逆和Backus - Gilbert反演理论，构造了用于河道糙率反演的牛顿 — 广义逆方法和自然逆方法，并推导了2种算法反演解估计的分辨率矩阵和单位协方差矩阵；Ding，Y.等[9]建立了基于误差最小化分析的有限记忆准牛顿法，并在浅水河道中进行糙率的反演分析；霍光等[10]首先采用多相模糊统计法确定河道糙率的一个小范围邻域，再采用决策方案优选法以进一步确定糙率优选值；Bilgil，A.等[11]将人工神经网络法应用于河道糙率的优化率定，得到了较好试验结果；吴晓玲等[12]将卡尔曼滤波技术用于河道糙率的实时修正以提高了洪水预报精度；辛小康等[13]尝试建立基于改进遗传算法的河网糙率反演模型；李丽等[14]测试了自适应随机搜索(ARS)算法在资料受限条件下河网模型糙率反演的表现，得到了较理想的反演效果；陈一帆等[15]从河道糙率空间分布特性和专家经验知识2方面出发，分别提出了糙率空间分布缓变性和糙率经验估值2种先验知识，用于天然河流的糙率反演；包红军等[16]以糙率修正量为状态变量，观测值与模拟值之差为量测变量，建立了基于卡尔曼滤波的河道糙率反演模型；陈素红等[17]建立了基于多亲遗传算法的河道糙率率定模型，将其应用南水北调中线工程总干渠的部分渠道断面糙率的率定；陈一帆等[18]以糙率和水力状态量作为河网非线性动态系统状态变量，采用扩展卡尔曼滤波构建了结合糙率动态校正的河网水情数据同化模型，分析了水位动态噪声水平、糙率动态噪声水平、糙率初始值及测站个数对模型校正的影响。

4 河道糙率优化反演方法评价标准

在现有河道糙率反演方法中，多数反演模型以最小化观测值与模拟值之差作为模型的目标函数，研究如何能够搜索到目标函数的最优值，但对模型的数值稳定性、结果的合理性等反演特性考虑并不多。评价河道糙率反演方法性能的主要标准包括以下3方面。

4.1 初始值影响评价

对于欠定或混定的反演模型，反演结果受初始条件的影响较大，经常会因初值给得不恰当而出现结果发散的现象或者得到不同的反演结果。一个稳定的数学模型或数值求解模型应该能在不同初始条件下给出相近甚至相同的结果，它包括2个方面的意义[15]：①从数学模型的角度来讲，不会因为初值选取的原因而导致不同解，即满足解的唯一性；②从数值求解的角度来讲，不会因为初值选取的原因而导致计算结果失效或发散。

4.2 监测信息量影响评价

实际工程中，能够用于糙率率定的水文监测信息往往较少，导致反演模型常为欠定或者混定。对于一个稳健的反演模型而言，它应具有较好的鲁棒性，即在可用监测信息量较少时亦能给出较为合理的反演结果，并随信息量的增加，反演结果逐渐逼近于真实解[15]。监测信息的增加有2种方式：①单个观测站点时间维信息量的角度，增加其历时观测数据；②从河网空间维的角度来讲，增加观测站的布置个数。

4.3 信息误差影响评价

在真实世界中，观测资料总是存有误差。而误差的存在可能会使反演结果不合理，难以反映河道真实糙率。对于一个稳健的反演模型而言，它应具有较好的误差抗噪性，即在一定监测误差范围内能够给出较为合理的反演结果，不因微小的扰动导致巨大的数值振荡[15]。

5 河道糙率优化反演面临的困难与挑战

在回顾国内外研究现状的基础上，结合客观现实，认为当前河道糙率优化反演面临的困难和挑战主要包括以下几点：

（1）资料不完备。资料是反演分析的基础，是制约反演分析的一大瓶颈，一般很难全面详尽地获取河流相应的充足信息，且资料精度也难以得到保证，如断面测量精度粗略、水力要素历史观测资料短缺、水工建筑物调度情况不明等等。

（2）水力要素观测资料存在干扰和误差。这可能使得优化反演不易稳定，即观测数据中微小误差可能导致反演过程的较大振荡、反演结果的较大变动，因此在进行糙率优化反演时，尽可能引入糙率先验知识（包括糙率时空分布特性、糙率经验估值等信息），以减少反演过程的振荡性，提高结果的合理性及可靠性。

（3）糙率反演问题是多类型参数共同率定的反问题。在现有河网水力参数反演模型中，多数反演模型仅考虑河道糙率的率定，很少同步考虑水利工程过流特征参数的率定。然而，河网内往往存在一定数量的水利调控工程，其是河网防洪除涝系统的重要组成部分，对水流运动影响较大。若忽视水利调控工程过流特征参数的率定，将难以保障河道糙率反演结果的合理性。

（4）糙率反演问题是空间相关的反问题。河道糙率沿着河流流向不断变化，将其在空间方向上离散后，需要辨识的参数较多。然而，由于种种因素的限制，布置在河流上的水文测站通常比较稀疏，水文测站的个数往往少于河道糙率的个数，因而所建立的河道糙率反演模型通常是欠定的，加之缺乏糙率先验知识的应用，极易因观测误差或数值扰动导致糙率反演失败。

（5）糙率反演问题是时间相关的反问题。河流水情状态随着时间不断变化，而河道糙率及水利调控工程过流特征参数往往随着水位的变化而变化，表现为一个过程，若按过程辨识的思维方式进行水力参数的反分析，将不可避免地出现维数灾难。在现有研究成果中，多数反演模型将河道糙率或水利调控工程过流特征参数视为定值，进行参数静态反演，较少考虑参数的时间变化性，即参数的动态反演问题。

6 结 语

（1）由于水文测站数量有限或空间布置不合理，导致水情监测信息量难以满足河道糙率反演的需求，加之监测信息往往存在干扰和误差，这些都会使优化反演不易稳定、反演结果缺乏合理性，且监测数据中微小误差可能导致反演过程的较大振荡。因此，探索研究河道糙率先验知识，建立具有一定物理意义的糙率修正机制，用于解决水情监测数据不足条件下反演结果的不确定性，以期提高河道糙率反演过程的鲁棒性和反演结果的合理性，将是河道糙率反问题研究的发展方向之一。

（2）河道糙率往往随时间不断变化，如河道冲淤等下垫面变化引起的糙率变化、糙率随水位涨落的变化等，然而当前多数河道糙率反演模型将河道糙率视为定值，进行糙率静态反演，较少考虑糙率的时间变化性。因此，研究和解决河道糙率动态反演问题，体现糙率的时间可变性将是河道糙率反问题研究的发展方向之一。

（3）河道糙率的率定，不仅要考虑糙率本身的率定，还要考虑水利工程过流特征参数的率定。然而，河道糙率和水利工程过流特征参数在进行共同反演时，由于量纲、数量级、量变范围的不同，极易引起反演过程出现剧烈振荡，从而背离实际情况，使后续计算失效。因此，探索研究河道糙率和水利工程过流特征参数之间的反演机理和作用效应，提出合理可行的共同反演方法，将是河道糙率反问题研究的发展方向之一。

[1] Becker L，Yeh W W G．Identification of multiple reach channel parameters[J]．Water Resources Research，1973，9(2)：326 - 335．

[2] Wasantha Lal A M．Calibration of riverbed roughness[J]．Journal of Hydraulic Engineering，1995，121(9)：664 - 671．

[3] ATANOV G A，EVSEEVA E G，MESELHE E A．Estimation of roughness profile in trapezoidal open channel[J]．Journal of Hydraulic Engineering，ASCE，1999，125(3)：309 - 312．[4] Khatibi R H，Williams J J，Wormleaton P R．Identification problem of open - channel friction parameters[J]．Journal of Hydraulic Engineering，1997，123(12)：1078 - 1088．

[5] Ramesh R，Datta B，Bhallamudi S M，et al．Optimal estimation of roughness in open - channel flows[J]．Journal of Hydraulic Engineering， 2000，126(4)：299 - 303．

[6] 董文军，姜亨余．一维水流方程中曼宁糙率的参数辨识[J]．天津大学学报(自然科学与工程技术版)，2001，34(2)：201 - 204．

[7] 李光炽，周晶晏，张贵寿．用卡尔曼滤波求解河道糙率参数反问题[J]．河海大学学报(自然科学版)，2003，31(5)：490 - 493．

[8] 程伟平，刘国华．基于广义逆理论的河网糙率反演研究[J]．浙江大学学报，2005，39(10)：1063 - 1068．

[9] Ding Y，Wang S S．Identification of Manning’s roughness coefficients in channel network using adjoint analysis[J]．International Journal of Computational Fluid Dynamics，2005，19(1)：3 - 13．

[10] 霍光，王义刚．基于多因素模糊综合评判的河网糙率求解 [J]．河海大学学报(自然科学版)，2006，34(5)：518 - 521．

[11] Bilgil A，Altun H．Investigation of fl ow resistance in smooth open channels using artif i cial neural networks[J]．Flow Measurement and Instrumentation，2008，19(6)：404 - 408．

[12] 吴晓玲，王船海．基于水动力学模型的实时糙率反推在洪水预报中的应用[J]．水电能源科学， 2008，26(5)：43 - 45．

[13] 辛小康，刘刚，张向东，等．基于遗传优化的河网数学模型糙率参数反演[J]．水利水电科技进展， 2009， 29(6)：21 - 24．

[14] 李丽，王加虎，王建群，等．自适应随机搜索算法在河网数学模型糙率反演中的应用[J]．水利水电科技进展，2011，31(5)：64 - 67．

[15] 陈一帆，程伟平，蒋建群．一种稳健的河流糙率反演方法[J]．浙江大学学报(工学版)，2013，47(8)：1361 - 1365，1378．

[16] 包红军，赵琳娜．基于Kalman滤波糙率反演模型的河道洪水实时预报研究[J]．水力发电学报，2012，31(3)：59 - 64．

[17] 陈素红，刘孟凯，邢领航．基于多亲遗传算法的渠道非恒定流糙率率定模型及其应用[J]．水电能源科学，2013，31(5)：81 - 83．

[18] 陈一帆，程海洋，万晓丽，等．结合糙率校正的河网水情数据同化[J]．水科学进展．2015，26(5) ：731 - 738．

（责任编辑 姚小槐）

Inverse Problems of River Roughness: Research Review and Prospect

SHEN Wu - wei1，2，CHEN Yi - fan1，2，SHEN Zhen - dong1，2
(1. Zhejiang Institute of Hydraulics & Estuary，Hangzhou 310020，Zhejiang，China；2. Zhejiang Guangchuan Engineering Consultation Co., Ltd., Hangzhou 310020，Zhejiang，China)

River roughness is a critical sensitive parameter of hydraulic calculation for rivers，which is a comprehensive one inf l uenced by many factors. Table - checking，formula，trial - and - error and other commonly used methods cannot meet the demands of hydraulic calculation. Therefore，the inversion theories and methods of river roughness have drawn extensive attention of scholars from home and abroad. After reviewing and summarizing the basic methods and research updates of inverse methods for river roughness，this paper brought forward the difficulties and challenges as well as prospective directions for future study in this fi eld.

river roughness；inversion analysis；roughness calibration

TV131.4

A

1008 - 701X(2017)04 - 0001 - 03

10.13641/j.cnki.33 - 1162/tv.2017.04.001

2016-02-21

国家自然科学基金资助项目(51609213)。

沈五伟(1983 - )，男，工程师，硕士，主要从事水文水动力学研究、水利工程规划设计工作。

E - mail：214884860@qq.com