贝叶斯计量经济学及面板数据中的贝叶斯推断
2010-05-18李小胜
李小胜
(安徽财经大学 统计系,安徽 蚌埠 233030)
0 引言
随着贝叶斯理论的发展和计算机模拟等数值计算技术的提高,贝叶斯技术已大量应用在各门科学当中,而把贝叶斯理论应用到计量经济学,是上世纪60年代以来在一大批统计学家和计量经济学家的共同努力下,迅速发展起来的。贝叶斯计量经济学的发展主要得益于60年代的Jacques Dréze,Tom Rothenberg,Walter Fisher,Albert Ando,Gordon Kaufman,Arnold Zellner等人。其中 Zellner的《An Introduction to Bayesian Analysis in Econometrics》一书的出版标志着贝叶斯计量经济学的真正诞生。该书较为全面地阐述了贝叶斯计量经济学的大多数专题。
随后出版的大多数计量经济学的教科书也都含有贝叶斯计量经济学的章或节,例如Maddala(1978),Intriligator(1978),Malinvaud(1980),Judge et al(1985),Chow(1983)的计量经济学教课书。相比60年代以前人们应用的非贝叶斯计量经济学的方法,这个方面的文献和书籍多了起来。Zellner(1985)对贝叶斯计量经济学理论发展进行了回顾,秦朵(Qin,1996)从另一个角度也进行了回顾。Poirier,D.J.(2006)更是对国外(1970~2000)几种重要的期刊使用贝叶斯方法在经济和计量经济学文章中的数量的发展速度进行了回顾。当代许多杰出的计量经济学家如Geweke,Litterman,Dempster,Sims,Maddala,Chib等都应用贝叶斯计量经济学。华人计量经济学家秦朵(1994)就应用贝叶斯计量经济学,李宏毅(1997)把贝叶斯计量经济学应用到面板数据分析当中。周国富(1990)把贝叶斯计量经济学应用到资产定价和资产组合中。而国内研究贝叶斯理论的人员很多,但是研究贝叶斯计量经济学的文献并不是很多,只有朱慧明(2006)研究了贝叶斯计量经济学的几个重要专题,并深入地进行了讨论。本文将首先比较经典学派与贝叶斯学派的异同;然后,给出面板数据中应用贝叶斯方法的一些优势与结果。
1 贝叶斯学派与经典学派之间的差异及其分析的优点
贝叶斯学派与经典学派之间主要差异是明显的。首先,两个学派的核心差别是对于概率的不同定义。经典学派认为概率可以用频率来进行解释,估计和假设检验可以通过重复抽样来加以实现。而贝叶斯学派认为概率是一种信念。结合这种信念加以假设检验(先验机会比),当数据出现以后就产生后验机会比。这种方法结合了先验和样本信息辅助假设检验。其次,两者差异体现在使用信息不同,经典学派使用了总体信息和样本信息,总体信息即总体分布或总体所属分布族的信息,样本信息即抽取样本(数据)提供给我们的信息。而贝叶斯学派除利用上述两种信息外,还利用了一种先验信息,即总体分布中未知参数的分布信息。两者在使用样本信息也有差异,经典统计对某个参数的估计θ^说是无偏的,其实是利用了所有可能的样本信息,贝叶斯学派只关心出现了的样本的信息。而且贝叶斯学派将未知参数看作是一个随机变量,用分布来刻划,即抽样之前就有有关参数问题的一些信息,先验信息主要来自经验和历史资料。而经典统计把样本看成是来自具有一定概率分布的总体,所研究的对象还是总体,而不局限于数据本身,将未知参数看作常量。
贝叶斯分析方法的优点也很多,与频率方法比较贝叶斯方法充分利用了样本信息和参数的先验信息,在进行参数估计时,通常贝叶斯估计量具有更小的方差或平方误差,能够得到更精确的预测结果;贝叶斯HPD(最大后验)置信区间比不考虑参数先验信息的频率置信区间短;贝叶斯方法能对假设检验或估计问题所做出的判断结果进行量化评价,而不是频率统计理论中的接受,拒绝的简单判断;在基于无失效数据的分析工作,贝叶斯统计有着重要优点(韩明,2005),一批产品中抽出10进行检验,若无不合格品时,经典统计认为次品率为0而贝叶斯统计得到的是1/12,可见贝叶斯估计更谨慎。
2 面板数据的贝叶斯推断
面板数据是用来描述一个总体中给定样本在一段时间内的情况,并对样本中每一个样本单元都进行多重观察。这样的数据在计量经济学中称为Panel Data,而统计学中称为Longitudinal Data。面板数据常用双下标变量表示。例如
yit,i=1,2,…,N;t=1,2,…,T
N表示面板数据中含有N个个体。T表示时间序列的最大长度。若固定t不变,yi.,(i=1,2,…,N)是横截面上的N个随机变量;若固定i不变,y.t,(t=1,2,…,T)是纵剖面上的一个时间序列(个体)。 Mundlak(1961)、Balestra 和 Nerlove(1966)最早把Panel Data引入到经济计量中。从此以后,大量关于Panel Data的分析方法、研究文章如雨后春笋般出现在经济学、管理学、社会学、心理学等领域。面板数据分析的文章可谓是浩如烟海,Baltagi与Hisao各自的书中都进行了回顾。
而上面的文章和书籍中的面板数据分析都是在频率学派的观点下阐述的,但是把Bayes方法融入面板数据的文章不是很多,且大多数文章只给出了在二次损失函数下的贝叶斯后验的均值和后验方差,并没有给出怎么得来的。本文就用贝叶斯方法来分析面板数据看其优势所在。面板数据的模型常用下式表示:
yit=ait+xitβit+εit(i=1,2……N;t=1,2,……T)
其中,Xit=(x1it,x2it,xkit)'是 k×1 的外生变量向量;βit=(β1it,β2it,βkit) 是 k×1 的参数向量;ait是截距项,k 为解释变量的个数ε;εit是k×1的误差扰动项(标量)。下标it表示第i个单位(个人、家庭、公司和国家等)在第t期的情况。
通常我们的假定是截距项和斜率项不随时间变化,而且斜率项通常又假定是不变的,截距项随个体不同而不同。有式:yit=ai+Xitβ+εit。 上式我们可以用一个向量来表示:y=Xβ+ε。其中我们假设ε~N(0,Ω),那么这个面板数据模型的y服从均值为Xβ,方差为Ω的正态分布y~N(Xβ,Ω)。在Ω已知的条件下我们可以应用广义最小二乘法的均值和方差的估计量,分别为:
β^=(X'Ω-1X)-1X'Ω-1y,Var(β^)=(X'Ω-1X)-1
由于ε到y的雅可比变换是一一对应的变换,所以似然函数为:
f(y|β,Ω)=(2π)-NT/2|Ω|-1/2exp{-(1/2)(y-Xβ)'Ω-1(y-Xβ)}
记 L(β,Ω)=(2π)-NT/2|Ω|-1/2exp{-(1/2)(y-Xβ)'Ω-1(y-Xβ)}=(2π)-NT/2|Ω|-1/2exp{-(1/2)(y-Xβ^)'Ω-1(y-Xβ^)+(β-β^)1X'Ω-1X(β-β^)}
由于:(y-Xβ)'Ω-1(y-Xβ)=(y-Xβ^)'Ω-1(y-Xβ^)+(β-β^)1X'Ω-1X(β-β^),贝叶斯分析中上述这个模型的先验假设大致可以分为四种:①已知 Ω 而 β 未知,我们假设 β 服从 π(β|Ω)~N(β0,Ω0);②Ω和β都未知,我们假设其服从模糊先验(Jeffreys先验)分布为:π(Ω)∝|Ω|-(p+1)/2;③已知 β 而 Ω 未知,我们假设其服从 π(Ω)~IWp(n,Ω0),IW 表示逆 Wishart分布。 维度为 p,自由度为n,Ω0为已知阵,又叫超参数;④Ω和β都未知,我们假设其服从共轭先验分布为:π(β|Ω)∝π(β|Ω)π(Ω),即 π(Ω)服从逆Wishart分布,π(β|Ω)表示给定Ω下的正态分布。本文只讨论第一种情况,第二种情况得到的后验估计与广义最小二乘法相同。第三种一般很少出现,方差信息都已知而参数还未知,一般不用。第四种情况由于超参数太多,一般只有理论上探讨的意义。所以若我们取β的先验分布为β~N(β0,H),那么先验密度函数为:
π(β)=(2π)-K/2|H|-1/2exp{-(1/2)(β-β0)'H-1(β-β0)
根据贝叶斯定理。后验密度似然函数先验密度。即π(β|y)=π(β)Lπ(β,Ω)。 有:
π(β|y)∝exp{-(1/2)[(β-β^)'X'Ω-1X(β-β^)+(β-β0)'H-1(β-β0)]}
上面的公式中我们已略去与β无关的项,[……]中可以表示为:
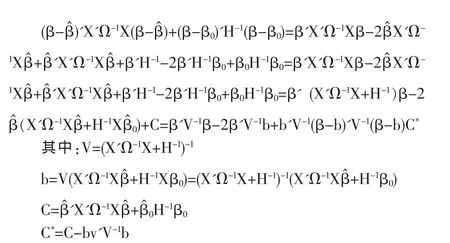
C*中不含有 β,那么最终后验密度为:π(β|y)∝exp{-(1/2)(β-b)'V-1(β-b)]},即 β~N(b,V),在二次损失函数下后验均值就是关于后验分布的期望值:
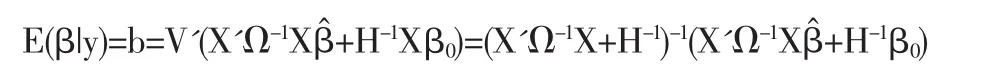
后验方差为:var(β|y)=V=(X'Ω-1X+H-1)-1
3 结论
从上面的均值和方差可以看出,面板数据的贝叶斯计量经济学的后验均值是广义最小二乘法和先验均值的加权,后验方差是先验方差和样本方差的加权;贝叶斯方法得到的均值和方差综合了先验信息、样本信息,使推断更为科学合理。
正如Zellner(1997)所说:在计量经济学中,经典学派不用先验信息是很难让让人相信的,他们常在想误差项是个什么分布,有无自相关,建立怎样的模型(是参数的,还是非参数模型),选择一个什么样的显著性水平,检验的势如何?例如经典学派在假设随机系数模型和时变参数模型,那么他们对参数分布作出的假定就相当于贝叶斯学派,给出参数的具体分布一样。当然贝叶斯学派的先验信息有时也是有很大局限性的,受个人知识和经验的影响,先验分布选择的带人为的主观性等,这也是经典学派不用贝叶斯方法的原因。总之,从上述分析可以看出,如果贝叶斯方法使用的恰当会使推断更为精确。
[1]刘乐平,袁卫.现代Bayes方法在精算中的应用及展望[J].统计研究,2002,(2).
[2]茆诗松.贝叶斯统计[M].北京:中国统计出版社,1999.
[3](美)普雷斯(S.James Press).贝叶斯统计学:原理、模型及应用[M].廖文等译.北京:中国统计出版社,1992.
[4]朱慧明,韩玉启.贝叶斯多元统计推断理论[M].北京:科学出版社,2006.
[5]方开泰.实用多元统计分析[M].上海:华东师范大学出版社,1989.
[6]韩明.基于无失效数据的可靠性参数估计[M].北京:中国统计出版社,2005.
[7]Balestra,P.,M.Nerlove.Pooling Cross-Section and Time-Series Data in the Estimation of a Dynamic Economic Model:The Demand for Natural Gas[J].Econometric,1966,34.
[8]Mundlak,Y.Empirical Productions Free of Management Bias[J].Journal of Farm Economics,1961,(43).
[9]Zellner,A.An Introduction to Bayesian Inference in Econometrics[M].Chichester:John&Wiley,1971.
[10]Press,J.S.Applied Multivariate Analysis:Using Bayesian and Frequentist Methods of Inference[M].Nelbourne:Krieger Publishing,1982.
