应对CDMA系统有界干扰的鲁棒自适应功率控制

吕文渊，韩存武，马鹏维，马海燕

(东华大学 信息科学与技术学院，上海 201620)

功率控制是无线移动通信的核心问题，与CDMA小区系统的容量与干扰是密切相关的，并且是一种提高系统容量、改善通信质量的有效途径。

到目前为止，已经提出了很多功率控制的算法。RINTAMAKI M、KOIVO H和 HARTIMO I提出了一种闭环系统中的自适应自校正控制器[1]，Seung-Ok Choi和Kwan-Ho You提出了在上行链路中，基于线性二次跟踪理论的自适应功率控制算法[2]。

本文提出了一种在系统存在有界干扰时的鲁棒自适应功率控制算法。先定义了1个由多路衰减效应引起的信道变量，为了得到这个变量的估计值，采用了带死区的最小二乘法。根据估计值，可以对用户在每一步的发射功率进行更新来达到期望的信噪比。最后，用广义最小方差算法来得到用户在每一步的发射功率的迭代公式。

1 系统模型

假设1个系统由K个基站和M个移动台组成[3]，以其中的1个基站作为目标基站。在基站k接收到用户i的信息比特能量(Eb)与干扰功率谱密度(M0)之比(信噪比)为：

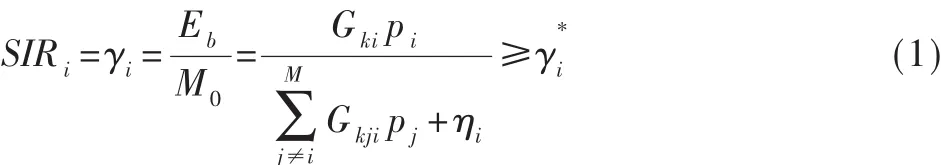
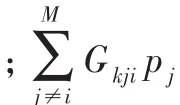
2 鲁棒自适应功率控制算法

定义：向量 p={pi}，η={ηi/Gki}；矩阵 H={Hij}，其中，Hij=Gkj/Gki，i≠j。 当 i=j时，Hii=0，则式(1)可写为如下的矩阵形式：

其中，I为特征矩阵。当式(2)取“=”时，求得的为最小功率。

为了求解式(2)，选用如下的迭代方法[4-5]：

其中，M和N是迭代矩阵，并且满足p*=M-1Np*+M-1η，p*是式(2)去“=”时的唯一解。

令 M=I，N=H，则得出经典功率控制算法[6]：

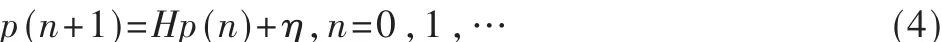
将(1)式代入(4)式，可得：

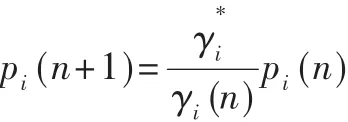
当系统存在有界干扰时，鲁棒自适应功率控制算法推导如下：

其中，ωd≤d为带有未建模动态的有界干扰。由带死区的最小二乘法可得θi(n)的最优估计值为：

其中，P(n)是 p×p 矩阵，P(n)的初始值 P(-1)是任给的正定矩阵。

如果在变量θi的条件下，在第n步达到了期望的信噪比γ*，那么就可以得到最优的功率 p*(n)=γ*×θ^(n)。由于变量θi不是固定步长，所以最优的发射功率在每一步都是不规则变化的。为了能够达到期望的信噪比，移动台必须按照最优功率值p*(n)来向基站发射功率。

定义状态方程为：

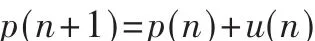
下面，用广义最小方差算法来求解u(n)。

定义：

加权二次型性能指标为：

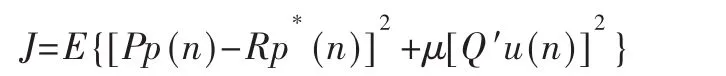
根据广义最小方差控制率，可以得出控制输入如下：

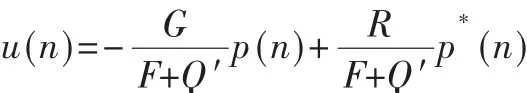
因此，可以得出：

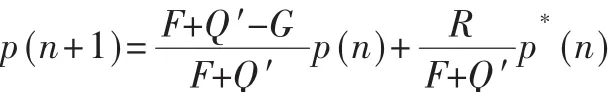
由于用户的发射功率受限于最大发射功率，即0≤p≤pmax，因此，每个用户的发射功率和信噪比表示如下：

3 仿真分析

利用上面所提出的2种算法，采用MATLAB作为仿真工具对其进行测试。

假设系统中有10个用户，用户目标信噪比为6 dB，系统的处理增益为68。

在系统所有用户发射总功率一定时，调整2种算法中系数因子，可以得出它们的信噪比性能比较如图1所示及发射功率比较如图2所示。通过仿真可以看出，本文提出的功率控制算法比传统的功率控制算法性能优越，使用户获得更高的信噪比，较低的发射功率，且系统容量得到了提高。

图1 传统的功率控制算法与鲁棒自适应功率控制算法信噪比性能比较

本文提出了1种鲁棒自适应功率控制算法，仿真结果表明，新算法比传统的算法起到更好的功率控制效果，可以有效地降低系统内干扰，大大提高系统容量。

图2 发射功率比较

[1]RINTAMAKIM， KOIVO H， HARTIMO I.Adaptive closed-loop power control algorithms for CDMA cellular communication systems[J].IEEE Transactions on Vehicular Technology， 2004，53(6):1756-1758.

[2]SEUNG-Ok Choi，KWAN-Ho You.Channel adaptive power control in the uplink of CDMA Systems[C].Wireless Personal Communications， 2008，47(3):441-448.

[3]ARIYAVISITAKUL S.SIR based power control in a CDMA system[C].Proc.IEEE GLOBECOM，1992:868-873.

[4]JANTTI R，KIM S L.Second-order power control[C].IEEE J.Select.Areas Communication， 2000，18(3):447-457.

[5]ZANDER J， KIM S L， ALMGREN M，et al.Radio Resource Management for Wireless Networks[M].2001.

[6]FOSCHINI G J，MILJANIC Z.A simple distributed autonomous power control algorithm and its convergence[C].IEEE Trans.on Vehicular Technology， 1993，42(4):641-646.