一种基于CL的新型可分电子现金系统

岳 璐，贾小珠，茹俊丽

(青岛大学 信息工程学院，山东 青岛 266071)

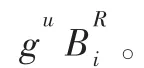
1 预备知识

1.1 符号定义

其中：G1、G2分别是基为素数p的循环群，它们可以相同也可以不同。

G1、G2、GT中的元素都有唯一的二进制表示。

g0、h0分别是群 G1、G2的生成元。

ψ：G2→G1是同构体 G2到 G1的映射，满足 ψ(h0)=g0。

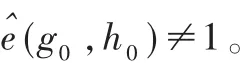
1.2 数学假设

1.2.1 DDH假设

循环群 G 上的 DDH 假设为：给定 g，ga，gb，gc，去判断gab=gc是否成立是困难的。其中，g为G的生成元，a、b、c 为随机数，满足 a，b，c∈{0，1，…，q-1}。 DDH 假设与解离散对数问题相关，因此，在循环群G中基于离散对数的困难性假设，DDH假设是成立的。

1.2.2 y-DDHI假设[6，13]

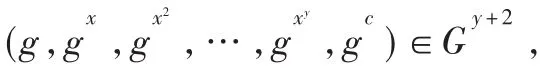
1.2.3 LRSW假设[14]

设 G=＜g＞是以素数 p 为底的循环群，u=gx，v=gy，Ou，v(·)满足对于 a∈G，m∈Zp能够计算得到(ay，ax+mxy)。素数群 G 上的 LRSW 问题指： 对于 g，u，v，Ou，v(·)，求(m，a，b，c)满足 m≠0∧a∈G∧b=ay∧c=ax+mxy，且 m 不是 Ou，v(·)的输入。 素数群 G上的 LRSW 假设指素数群G上的LRSW问题是难解的。

2 基于CL签名的压缩电子现金方案

2.1 银行初始化

λ为系统安全参数，(G1，G2)是双线性群组，同构体G1、G2满足|G1|=|G2|=p。

假设Gp是以p为底的群，且满足DDH假设。

设 H：{0，1}*→Zp是加密哈希函数。

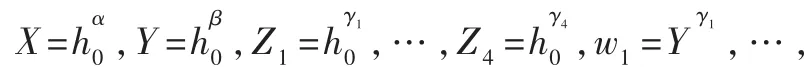
2.2 用户初始化

2.3 取款协议

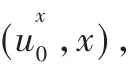
2.4 支付协议

设用户的电子钱包为(a，b，c，A1，A2，A3，A4，B1，B2，B3，B4，s，t，x，y，r，J)，其中，J≤k，商家身份为 I，并同意取款信息，计算 R=H(info，I)。

2.4.1 单一货币的支付协议

其中，δ2=1/r2mod p，δ4=1/r4mod p，δJ=Jx，δ5=r5x，δt=tx。

2.4.2 压缩支付协议

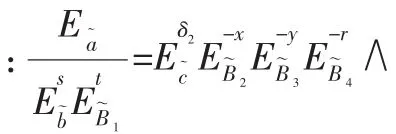
2.4.3 批处理支付

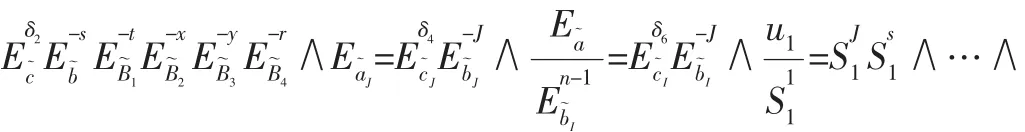
2.5 存款协议

商家发送给银行支付协议的复本，银行检验商家与用户交易的复本的正确性，为了防止用户和商家串通起来进行联合欺骗，银行需检验商家的身份I，确认R=H(info，I)没有被使用过，防止电子现金的重复花费。同时为了防止商家将1次交易的复本提交给银行2次，在确认 R=H(info，I)没有被使用过以后，银行将 S，T，R 存入自己的数据库。(如果是压缩支付，则银行对于i=1，…，k，计算 Si=Ved(s，i)，并将所有的(S，T，R)，(S，Tc，s，t，R)存入相应的数据库)。

3 非法用户的追踪

对于重复花费者的追踪：当银行收到一个新的支付协议的复本时，银行首先检查数据库中是否存在S，如果有，则说明重复花费了电子现金，银行对重复花费者按以下方式进行追踪。

(1)单个电子现金的重复花费

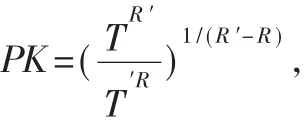
(2)压缩支付中和单个电子现金重复

设银行数据库中的记录为(S，Tc，s，t)，当前提交的新的复本为(S，T，R)，银行确认 i满足 Si=Vrf(s，i)，并计算PK=T/(Vrf(t，i)R)，找出非法用户，并进行惩罚。

(3)重复压缩支付

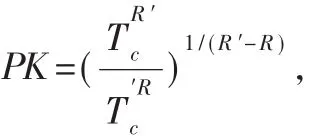
4 特性分析

(2)可分性。用户1次从银行取得n个电子现金放入自己的电子钱包，每当有支付请求时，取i个总和满足支付请求的电子现金进行支付，满足1次取款多次支付的要求，从而达到可分。

(3)高效性。系统基于CHL协议的设计思想，当用户能够计算得到Si和Ti，则直接提交相应的 s和 t。充分利用了CL签名的优点，除批处理支付协议外，其他协议均为常数级时间复杂度，而且，批处理支付协议的时间复杂度也与花费的电子现金的数目线性相关。因此，系统整体效率较高。

本文将压缩支付和批处理支付的思想融入到压缩型电子现金系统中，给出了运用这种思想的可靠电子现金方案，基于CL签名构建了一种安全高效的可分电子现金系统。但是，CL签名不支持并发签名，所以，提款协议必须按序进行。目前，在安全的压缩型电子现金系统中，设计并行取款的新型系统是下一步研究方向。

[1]NAKANISHI T， SHIOTA M， SUGIYAMA Y.An unlinkable divisible electronic cash with user’s less computations using active trustees[C].ISITA 2002，2002.

[2]CANARD S， GOUGET A， HUFSCHMITT E.A handy multi-coupon system[J].Applied Cryptography and Network Security-ACNS 2006， LNCS， 2006(3989):66-81.

[3]李梦东，杨义先.无可信第三方的离线电子现金匿名性控制[J].电子学报，2005，33(3):456-458.

[4]费雄伟，李乔良.一个新的安全且高效的电子现金系统[J].计算机应用研究，2008，25(5):1543-1545.

[5]BRICKELL E， GEMMELL P， KRAVITZ D.Trustee-based tracing extensions to anonymous cash and the making of anonymous change[C].In SODA ’95， Proceedings of the Sixth Annual ACM-SIAM Symposium on Discrete Algorithms.Society forIndustrialand Applied Mathematics，1995:457-466.

[6]CAMENISCH J， HOHENBERGER S， LYSYANSKAYA A Compact e-cash[J].In EUROCRYPT， LNCS， 2005(3494):302-321.

[7]CANARD S， TRAOR’E J.On fair e-cash systems based on group signature schemes.In ACISP，2003:237-248.

[8]AU M H，WU Q，SUSILO W，et al.Compact e-cash from bounded accumulator.In CT-RAS，2007.

[9]TERANISHI I，SAKO K.K-times anonymous authentication with a constant proving cost.In Public Key Cryptography，2006.

[10]CAMENISCHAND J，LYSYANSKAYA A.Signature schemesand anonymouscredentialsfrom bilinearmaps[J].In CRYPTO，2004(3152):56-72.

[11]AU M H，SUSILO W，MU Y.Constant-size Dynamic k-TAA[C].In SCN 2006，volume 4116 of LNCS.Springer-Verlag，2006.

[12]BONEH D，BOYEN X.Short signatures without random oracles[C].In EUROCRYPT 2004， Berlin， LNCS 3027，Springer-Verlag，2004.

[13]DODIS Y，YAMPOLSKIY A.A verifiable random function with short proofs and keys[J].In PKC 2005，volume 3386 of LNCS，2005:416-431.

[14]LYSYANSKAYA A， RIVEST R L， SAHAI A， et al.Pseudonym systems.In Selected Areas in Cryptography[J]，Lecture Notes in Computer Science，1999(1758):184-199.