ESTAR模型单位根检验的性质研究

袁 铭

（天津财经大学 理工学院，天津 300222）

0 引言

平滑转移自回归模型(STAR)是 Granger和 Teräsvirta于1993年提出的。作为机制转换类模型的一种，该模型的机制转换是平滑的，并且可以通过选取不同的转移变量和转移函数形式较为准确地捕捉经济过程中对称与非对称机制转换以及确定性趋势等现象，具有较高的灵活性。在此基础上，针对实证研究中经济时序普遍存在的非平稳现象，人们开始关注机制转换模型的单位根检验问题，相关的研究成果包括：Kapentanios和Shin[1]针对TAR模型提出了Wald类型的单位根检验，并通过Monte Carlo方法验证了它比DF统计量具有更高的检验功效，此后二人相继提出了针对多机制TAR模型以及指数平滑转移自回归模型（ESTAR）的单位根检验方法，推导出非线性ADF检验统计量的极限分布，并将其应用于实际利率实证研究；Pascalau[2]提出了基于F统计量的LSTAR单位根检验方法，使其能够解决机制转换的非对称问题；Rothe和Sibbertsen[3]则引入了非参数方法，提出了基于PP-Z统计量的ESTAR单位根检验。

本文将在上述研究的基础上，以ESTAR模型为代表，进一步研究非线性单位根检验的小样本特征，以及当误差项非独立同分布时两类检验的可靠性，以期为拓展STAR类模型在非平稳时序建模中的应用提供一定的理论支持。

1 STAR族模型的单位根检验

ESTAR模型的基本形式为：

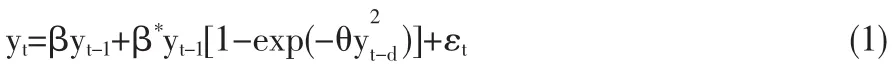
单位根检验的原假设与备择假设为：H0:β=1；θ=0；H1:θ＞0

在原假设成立的条件下。（1）式将退化为非平稳AR(1)过程yt=yt-1+εt；在备择假设成立下，ESTAR模型将转化为 yt=(β+β*)[1-exp(-θy2t-d)]yt-1+εt。若 yt-d=0 或者 yt-d→∞，则（1）式也会退化为近似AR(1)过程。同时，如果真实数据过程是平稳的，但呈现明显的非线性特征，则标准的线性ADF检验失效。

针对ESTAR模型的单位根检验问题，George Kapetenios和Phillips Sibbertsen分别提出了基于ADF-t统计量以及PP-z统计量的方法。这两种方法的核心思想都是在（1）式中令 β=1，d=1，并将按照一阶泰勒级数展开，从而构造检验辅助回归为Δyt=δy2t-d+εt。其中，非线性ADF-t统计量（NLADF-t）为：

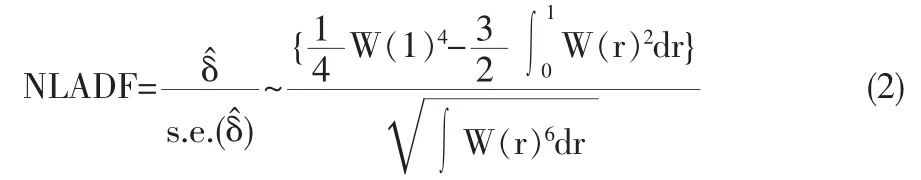
非线性PP-Z统计量（NLPP-Z）为：

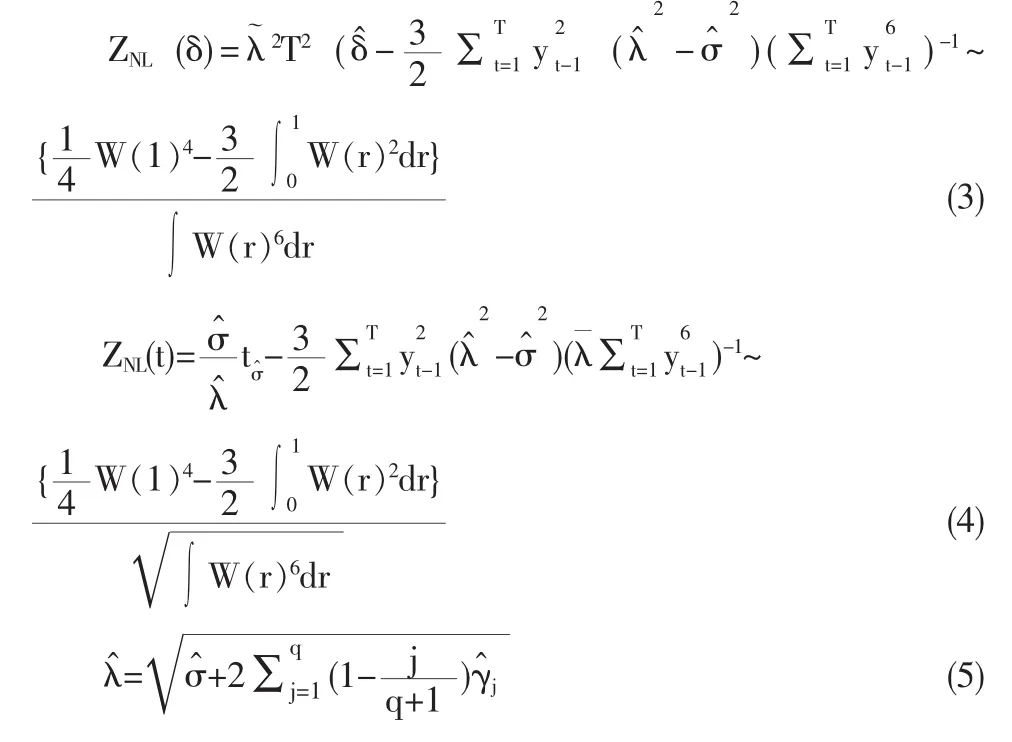
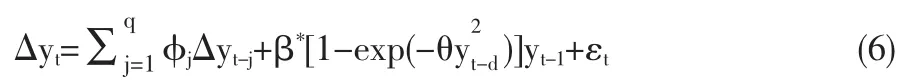
则可以使用如下辅助回归：

Kapentanios和 Shin[1]中指出，根据(7)式得到的 ADF(p)统计量与标准ADF检验拥有相同的渐进分布，并且在备择假设成立的条件下ADF(p)统计量是一致统计量。对于原始数据过程含有漂移项或者含有线性趋势的情况，可以参考Fuller的方法进行相应处理。（1）若原始数据包含漂移项 （记为Case 2），则可以针对原过程{xt}构造 yt=xt-μ，其中 μ 为{xt}的均值；（2）若原始过程同时含有线性趋势（记为Case 3），则可以构造其中对于是回归 xt=yt+μ+φt的 OLS估计量。表1给出了运用蒙特卡罗方法模拟100000次，在T=1000时三种情况下的临界值。

2 NLADF-t统计量与NLPP-Z统计量检验功效的比较

在STAR族模型实际应用中，特别在宏观经济过程建模中，样本容量较小（一般小于200），必然会对统计量的检验功效带来影响。因此，本节将通过模拟实验比较NLADF-t和NLPP-Z统计量的功效，进而比较二者在小样本下的可靠性。实验使用的数据生成过程为：

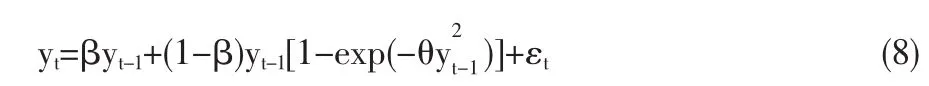
其中，β={0.2,0.5,0.8,0.9}，θ={0.05,0.1,1}，考察的样本容量分别为25、50、100。实验使用的名义水平均为5%，使用统计量的实际分位数作为临界值，模拟次数为10000。在检验设定方面，使用SIC信息准则来确定计算ADF统计量的滞后阶数，使用Newey和West[4]中的方法确定PP检验中的带宽以估计长期方差，最终得到的实验结果如表2所示，我们可以得出如下三个结论：

(1)总的来说，当θ较小时（此种情形在实证研究中较为常见），NLADF-t和NLPP-Z都比线性检验统计量优越，并且PP检验的功效要略高于ADF检验，显示出非参数方法在处理非线性时间序列问题时具有一定优越性。在小样本情况下，三种检验统计量的功效都很低，例如在T=25，β=0.9时，所有统计量的检验功效均小于0.15。虽然，Philips和Perron以及Schwett指出在线性单位根检验中也存在此现象，但非线性时尤甚。此外，表2中数据还显示非线性时间序列的单位根检验对样本容量的变化较为敏感。

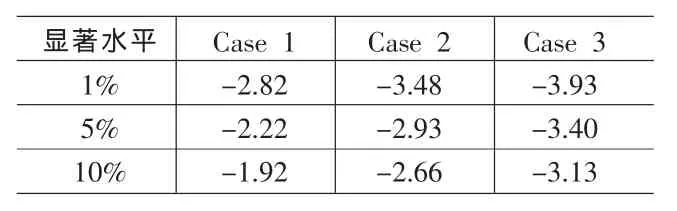
表1 不同情形下，ESTAR模型单位根检验临界值表

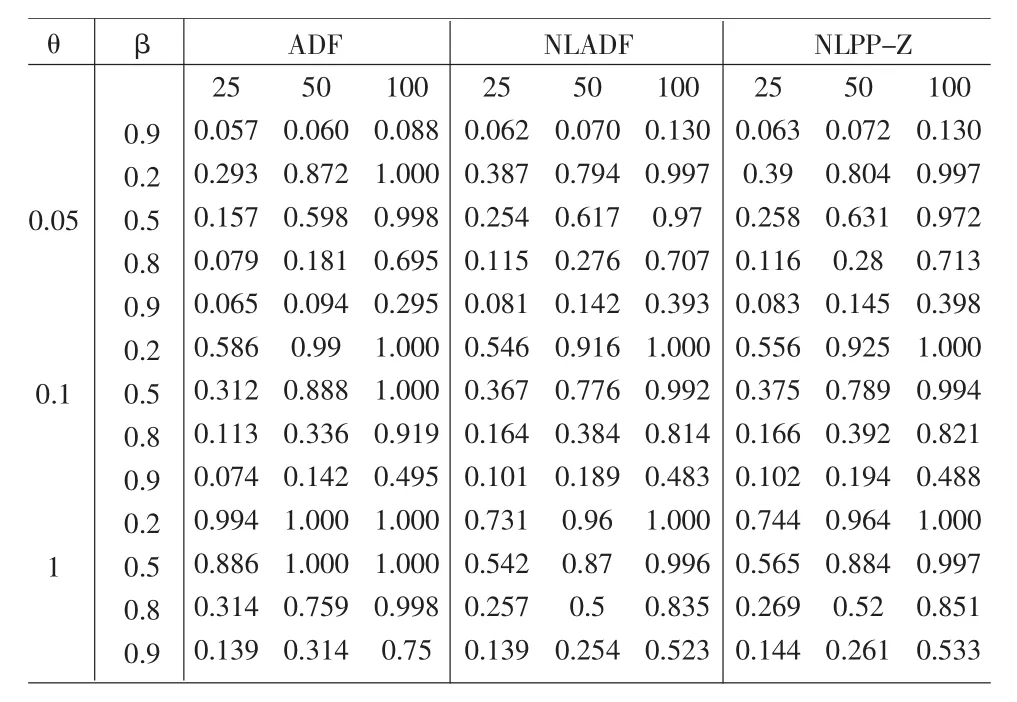
表2 小样本容量下NLADF、ADF、NLPP-Z统计量检验功效的比较

(2)θ对检验功效的影响。在各种样本容量下，三种统计量的检验功效都随着θ值的增加而提高。但当θ值较大时，ESTAR模型将退化为AR(p)模型，因此NLADF-t或者NLPPZ的功效反而不如线性ADF统计量。

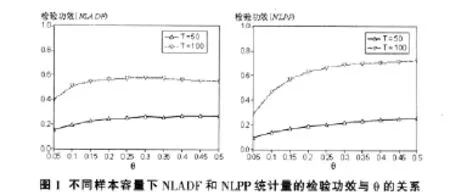
(3)样本容量对检验功效的影响。线性ADF-t统计量对样本容量的变化反应最为敏感，显示出两种非线性统计量在稳健性方面具有一定优势。同时，θ值对检验功效的影响也随着样本容量发生变化，图1给出了这一现象的直观说明；当θ值和样本容量都较大时，线性ADF-t统计量具有最高的检验功效，说明非线性过程逐渐呈现近似线性的特征。

3 误差项存在序列相关时非线性单位根检验的可靠性

下面研究在小样本情形下，当误差项为MA(1)过程时，NLADF-t统计量和NLPP-Z统计量的实际检验水平和检验功效，实验使用的数据生成过程与公式（8）相同，误差项的数据生成过程如公式（9）。

其中，ψ的参数集为{-0.8,-0.5,-0.2,0,0.2,0.5,0.8}，研究检验功效时，令 β=0.9，θ={0.01，0.05，0.1}，样本容量设定为100。NLADF检验滞后阶数的确定和NLPP检验带宽的确定与第2节相同。表3给出了三种统计量在不同θ值和ψ值下的检验功效，图2给出了实际水平随ψ值的变化规律。从表3和图2可以得出如下两个结论：

(1)检验水平方面，当|ψ|较大时，三种方法都表现出明显的扭曲（具体表现为水平过甚），随着|ψ|降低，水平扭曲程度也随之降低，并逐渐接近名义检验水平。本文还发现这种扭曲是非对称的，即ψ＜0时水平扭曲要甚于ψ＞0时的情况。在方法间比较方面，当|ψ|较小时，三者可靠性相近；当|ψ|较大时，NLPP统计量可靠性最差，ADF和NLADF统计量性质相近，前者在强序列相关时（|ψ|＞0.6）可靠性略优于后者。

(2)检验功效方面，三者表现出与检验水平间的权衡关系，即检验水平较高，检验功效也相应较高，θ对检验功效的影响与第2节得出的规律相似。需要注意的是，ψ对功效的影响随着θ值变大而降低。

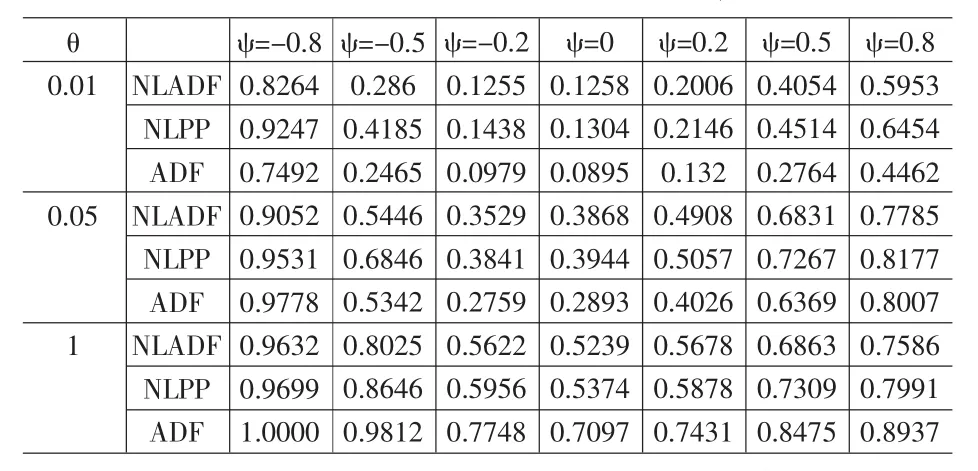
表3 NLADF、NLPP和ADF统计量的检验功效与ψ的关系

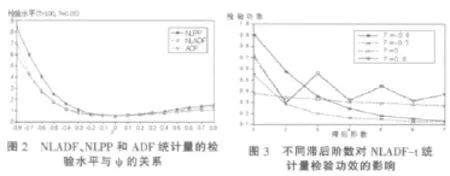
为了研究滞后阶数对NLADF统计量功效的影响，本文再设计一组实验。实验的相关设定为：T=100，β=0.9，θ=0.05，滞后阶数l={1,2,3…,7}，得到的实验结果如图3所示，我们可以得出如下规律：当ψ≤0时，随着l的增加，NLADF的检验功效单调下降，并且|ψ|越大，检验功效衰减的速度就越快；当ψ＞0时，检验功效呈现交替升降的情况，并且呈现收敛于某一稳定水平的趋势。

4 误差项存在异方差时非线性单位根检验的可靠性

Van Dijk和Terasvirta[5]指出微观金融市场时序建模将会成为STAR模型未来研究的热点问题。这类序列中普遍存在异方差现象。因此本节以概括能力很强的GARCH(1,1)模型为代表，研究误差项存在异方差时STAR模型单位根检验的可靠性。实验使用的数据生成过程与公式（8）相同，误差项的数据生成过程如公式（10）。

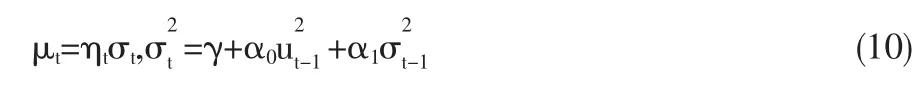
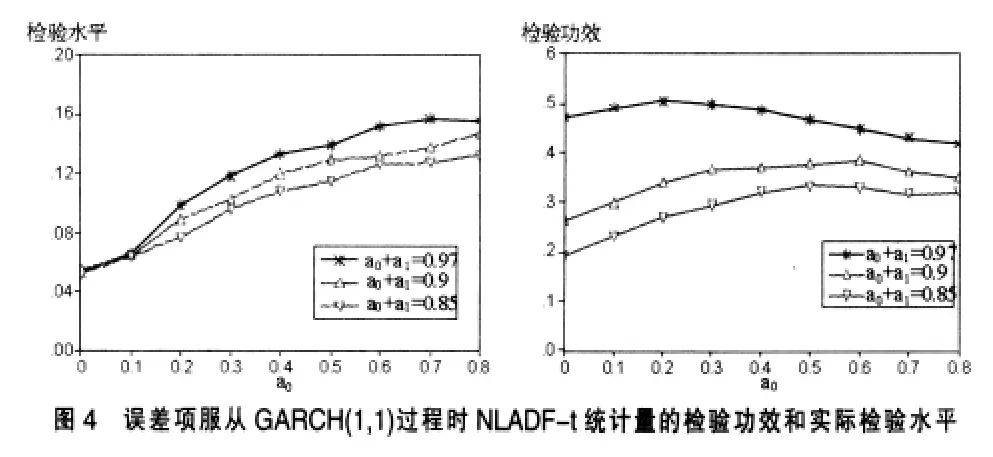
本文将样本容量设定为100，研究检验功效时，固定β=0.9，θ=0.05。实验主要考察GARCH过程单整程度就波动参数α以及非线性参数θ的影响，因此将参数集合设定为：α0+α1={0.97,0.9,0.85}，α0={0，0.1,0.2,…,0.8}，固定 γ=0.05。 在研究非线性参数θ的影响时，固定α0=0.3，θ={0.05,0.1,0.2,…，0.9}。由于篇幅所限，本文只研究NLADF统计量的可靠性，得到的结果如图4和图5所示，我们可以得到如下结论：

(1)在单整程度相同时，NLADF统计量的检验水平随波动参数α0增加而增加，而功效却表现出不同的特征，即随着α0先上升而后向下弯曲，并且曲线顶点位置取决于GARCH过程的单整程度。

(2)GARCH过程的单整程度与统计量的功效正相关，这一特征在α0较小时表现得尤为明显。当α0→1时，不同单整程度的功效曲线呈现收敛趋势。在检验水平方面，当α0＜0.1时，不同单整程度下的水平基本无差异。当α0＞0.1，水平扭曲程度随单整程度增加而增加。

(3)随着非线性参数θ的增加，NLADF-t统计量的功效呈现先增加而后趋于平稳的特征，并且检验功效的变化程度与GARCH过程的单整程度密切相关，这一点在θ＜0.4时表现得尤为明显。图5还显示θ对实际检验水平影响微弱，当α0+α1=0.97和α0+α1=0.85时，检验水平分别围绕0.12和0.09波动。

5 结论与展望

本文研究了基于ESTAR模型的非线性单位根检验NLADF和NLPP统计量的小样本特征，并以MA(1)和GARCH(1,1)为代表研究误差项分别存在序列相关和异方差时，序列相关程度ψ和单整程度对单位根检验的水平和功效的影响。未来的研究工作将围绕以下三方面展开：（1）为了拓展STAR模型在微观金融市场建模领域的应用，进一步拓展误差项存在异方差时检验可靠性研究的范畴，例如描述收益率序列非对称性的EGARCH和长记忆性的FIGARCH；（2）参考本文的结构研究LSTAR模型单位根检验的性质，并与ESTAR模型时得出的主要结论对比，分析二者差异；（3）构造基于模拟的单位根检验框架，例如Block Bootstrap和Sieve Bootstrap，以期能够修正渐近检验的水平扭曲。

[1]Kapentanios G,Y Shin.Testing for a Unit Root Against Nonlinear STAR Models[Z].Unpublished Manuscript,UniversityofEdinburgh，2000.

[2]Pascalau.Testing for a Unit Root in the Asymmetric Nonlinear Smooth Transition Framework[C].Working Paper，2007.

[3]Rothe，Sibbertsen.Phillips-Perron-type Unit Root Tests in the Nonlinear ESTAR Framework[J].ASTA Advances in Statistical Analysis,2006，（3）.

[4]Newey W,WestK.A Simple,Positive Semi-Definite,Heteroskedasticity and Autocorrelation Consistent Covariance Matrix[J].Econometrica,1987,55(3).

[5]Van Dijk，Terasvirta T.Smooth Transition Autoregressive Models—A Survey of Recent Developments[R].Econometric Institute Research Report EI2000-23/A，2000.