风险决策中时间压力影响的理论分析

王洪利

（1.西安交通大学 管理学院，西安 710000；2.中原工学院 经济管理学院，郑州 450007）

1 相关理论

1.1 风险决策

所谓决策风险，是指在决策活动中，由于主、客体等多种不确定因素的存在，而导致决策活动不能达到预期目的的可能性及其后果。时间压力下的风险决策是指决策者的决策行为受到决策时间的限制，要求决策者在规定的时间内作出决策行为。对于风险决策的理论分析和研究中比较著名的是期望效用理论。期望效用函数理论是20世纪50年代,冯·纽曼和摩根斯坦(Von Neumann and Morgenstern)在公理化假设的基础上建立的。期望效用理论认为，期望效用函数如下：

如果某个随机变量X以概率Pi取值xi，i=1,2,…,n，而某人在确定地得到xi时的效用为u(xi)，那么，该随机变量带给此人的效用是：

U(X)=E[u(X)]=P1u(x1)+P2u(x2)+...+Pnu(xn)

其中，E[u(X)]表示关于随机变量X的期望效用。因此U(X)称为期望效用函数，又叫做冯·诺依曼—摩根斯坦效用函数（VNM函数）。

1.2 贝叶斯风险决策概述

1.2.1 概念和步骤

（1）概念：根据各种事件发生的先验概率进行决策一般具有较大的风险。减少这种风险的办法是通过科学实验、调查、统计分析等方法获得较为准确的情报信息，以修正先验概率。利用贝叶斯定理求得后验概率，据以进行决策的方法，称为贝叶斯决策方法。

（2）步骤：

①进行预后验分析，决定是否值得搜集补充资料以及从补充资料可能得到的结果和如何决定最优对策。

②搜集补充资料，取得条件概率，包括历史概率和逻辑概率，对历史概率要加以检验，辨明其是否适合计算后验概率。

③用概率的乘法定理计算联合概率，用概率的加法定理计算边际概率,用贝叶斯定理计算后验概率。

④用后验概率进行决策分析。

1.2.2 贝叶斯定理

两事件的乘法法则：P（A1B）=P（A1）P（B/A1）

边际概率：如果事件A1和A2是互斥完备的，则

P（B）=P（A1）P（B/A1）+P（A2）P（B/A2）

两事件的贝叶斯定理公式：如果事件A1和A2是互斥完备的，其中某个事件的发生是事件B发生的必要条件。则

n个事件的贝叶斯定理公式：如果事件A1,A2，…，An是互斥完备的，其中某个事件的发生是事件B发生的必要条件。则

1.3 传统经济学的时间贴现

传统经济学假定效用是随时间以指数贴现的，其效用最大化问题表示为：

maxU=∑δtU(Ct)

其中

上式中，ρ为时间贴现率，δ指以指数曲线贴现的贴现系数，Ct为时间t某个事件的价值，U(Ct)为Ct在时间t的效用值。

2 时间压力对风险决策信息搜寻的影响

2.1 决策时间的效用

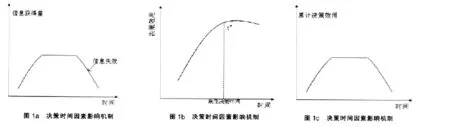
很多实验和数据表明，决策的边际时间效用在一定的时间段是递增的，但到达一定高峰后，随着时间的增加，边际时间效用就会停止不动甚至开始递减（见图1b），因此累计的决策时间效用会随着时间的增加先增后减（见图1c）。即一个决策过程存在一个最佳的决策时间点。原因可能是多方面的，因为决策受到决策任务特征，决策环境和决策者个人因素的影响。其中一个比较直接的原因在于决策中的信息影响，随着时间的增加各种因素导致决策中信息搜索量的变化规律为先增加后减少（见图1a）。

最佳决策的时间点是存在的，主要原因在于：首先，随着时间的增加成本是增加的，处理时间的增加，成本会越变越大，但收益是有限的，决策主体所能获取的收益不能够随着时间同比例增长或者可能停止增长甚至递减。所以不断的增加处理时间将带来收益的递减，直接导致效用的减少；其次，随着时间的增长，决策环境的变化可能会很大，但是决策者的信念的变化是一个很复杂的过程，不可能及时地随着决策环境的变化而变化。所以，无穷尽的增大决策时间，反而会使人的信念有可能偏离原来的决策环境，而使决策变得没有现实意义。第三，决策时间的延长，决策者收集信息和考虑方案会更充分，但是过度的延长决策时间会增加一些额外的干扰因素，这些很可能被决策者误认为是重要因素而将其加入到自己的信念中去，这被称为过度思虑。所以，无限的延长决策时间，并不会提高决策效用，反而会增加无谓的心理偏差和行为偏差。最佳决策时间点如图1b所示。

2.2 时间对决策中信息获取的影响

根据Hartley的信息公式[3]:

I=logN

其中I表示确定N个等概率事件中的一个出现时提供的信息。如果事件y把不确定范围从N1个缩小为N2个，那么信息就等于

这个公式被称为Hartely相对信息公式。

用Hartley公式计算信息，要求N个事件是等概率的,即P=1/N，但是通常的情况并不如此[4]。这时候我们用实际的概率代替假设的相等的概率，即用P1代替1/N1,用P2代替1/N2。于是，Hartley信息公式就变为[5]：

I=log(1/P)

上面的相对信息公式就变为：

在考虑时间压力的情况下，把客观事件集合A={x1,x2,…}中的一个表示为xi；把T={Tx,x=1,2,3,…,n}时刻的决策者获得的信息(message)集合中的一个表示为，那么T时刻提供的关于xi的信息就是：

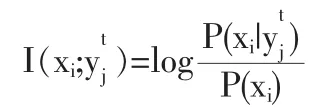
其中 P(xi)是 xi发生的先验概率，P(xi|yj)是 yj发生后 xi的条件概率。因为有Bayes公式

所以有

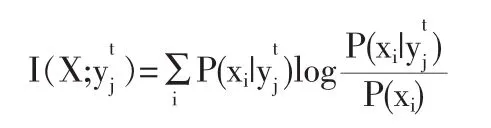
进一步求平均，得到T时刻YT提供关于X的平均信息：

其中H(X)和H(X|Y)分别是Shannon熵和Shannon条件熵：

现在我们进一步考虑时间压力的影响，设在不同的时间 Ta和 Tb（Ta＜Tb）时刻的决策者获得的信息(message)集合分别为由于决策时间的限制和影响，在此有BTa≠BTb。即决策者在不同的时间限制条件下，所获得的信息量是有差异的。因为决策者在时间压力条件下，受到做出决策的情绪压力和信息搜寻的时间的限制，导致了决策者信息搜寻量的差异。这种差异直接导致获得信息量的多少。

根据上面的公示，进一步求得，得到时刻Ta和Tb时刻的提供关于X的平均信息差异：

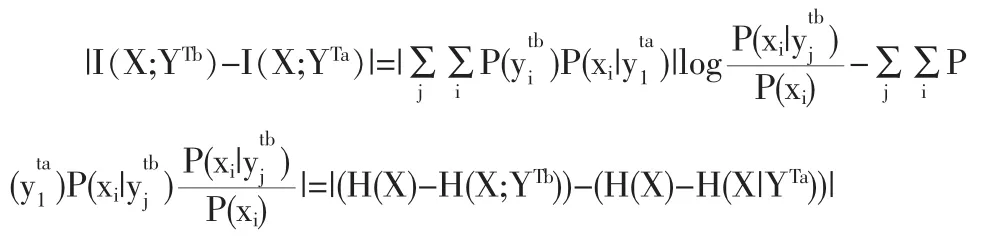
3 时间压力影响下的风险决策

3.1 时间压力下停止信息搜寻的条件分析

信息的价值在于其能提供的决策信息的收益高于为获取信息所付出的花费。如果补充新信息的成本小于完全信息的价值（任何信息的价值均小于完全信息的价值），则可认为这种补充信息的价值是合算的。

根据期望理论和传统经济学效用是随时间以指数贴现的假定，定义在Tb-Ta这段时间中，时刻Ta和Tb时刻的提供关于 X 的平均信息差异|I（X;YTb）-I（X;YTa）|的期望收益增加的函数为：

其中把客观事件集合A={x1,x2,…}中的一个表示为xi。

上面的平均信息差异公式考虑了时间的贴现效用，对时间的价值以现在时间为参照点，从决策者的价值出发，具有更大的客观性。

在时间限制条件下，如果超时决策会带来一定的损害后果，这种损害后果表现为一种惩罚。和我们对时间的机会成本的理解类似。如每延时一定的时间从总收益扣除k%，如总延时超过一定的期限，则扣除全部总收益，或总收益变为负值，表现为损失，则扣除比例R（超过时间限定的惩罚条件）其可用以下公式表示：

其中，Tl=TL+l-TL=TL+2l-TL+l=…=TLmax-TL+(N-1)l=ΔT，TL为决策的时间限制，在此限制时间内，决策时间的延长不带来的收益的损失，TLmax也可理解为决策强制终止时间，当T＜TL时，信息搜寻时间的增加不会带来对收益的惩罚。在此时间限定内我们考虑是否继续进行信息搜寻的条件是信息搜寻的成本和收益的差值。

当TL＜T＜TLmax时，我们还应进一步考虑决策时间的延长带来的收益的损失（惩罚）。即总损失为：

其中Ci为信息搜寻的成本。

即此时是否进行信息搜寻的条件是比较ΔU和LT的差值。如果 ΔU-LT＞0，则应该进行信息搜寻。如果 ΔU-LT＜0 则停止信息搜寻。

3.2 时间压力下风险决策的信息修正过程

时间压力下风险决策的信息修正过程由补充新信息、计算修正概率、重新决策和计算补充信息的价值四部分组成。

3.2.1 补充新信息

在时间限定条件下，通过信息搜寻得到新信息，获取条件概率。

3.2.2 计算修正概率

利用贝叶斯公式计算：

（3）根据（2）的后验概率，计算各方案的期望收益:

E(dj|Ai)=ΣP（Ai|Bj）Uij，maxE(dj|Ai)=E(djk|Ai)

(4)当T＜TL时，计算补充信息的期望价值，并和信息获取的成本进行比较以进行决策：

Es=ΣP(xi)E(xi)

当TL＜T＜TLmax时，则根据时间压力下停止信息搜寻的条件分析而进行决策。

4 结束语

本文从理论的角度详细分析了时间压力对风险决策的影响。从Hartley的信息公式出发，根据期望效用理论，考虑时间的贴现效用，从理论上研究了时间对决策中信息搜寻的影响，分析了时间压力下停止信息搜寻的条件。时间压力影响了人们的信息搜寻和获取量，理论上人们的信息搜寻有一个最佳的停止时间，而且其取决于不同的时间压力。本文给出了时间压力下风险决策的信息修正过程，得出了相关结论和需进一步分析的问题。

[1]郭仲伟.风险分析与决策[M].北京：北京机械工业出版社,1986.

[2]董志勇.行为经济学原理[M].北京:北京大学出版社,2006.

[3]Hartley,R.V.L.Transmission ofinformation[J].Bell System Technical Journal，1928，（7）.

[4]晨光.广义熵和广义互信息的编码意义[J].通信学报,1994，5（6）.

[5]Lu,Chenguang.A Generalization of Shannon's Information theory[J].Int.J.of General Systems,1999，（6）.