内河航道船舶航行操纵平面二维数值模拟初步研究

刘万利，张 波，伍文俊，余新明，李一兵，黎国森

（1.交通部天津水运工程科学研究所工程泥沙交通行业重点实验室,天津 300456；2.长江航道局，武汉 430010）

随着国家对内河水电枢纽工程、航道工程投入的加大，尤其是“十一五”期间长江黄金水道等水运主通道的建设，内河航道通航能力将不断提高，通航船舶吨位及船舶数量将大大增加，这就给航道或通航建筑物等的通航条件提出了更高的要求。另一方面，跨越通航河流的桥梁逐渐增多，给船舶通航及桥梁自身带来安全隐患。

以往大多采用物理模型结合自航船模的技术手段对航道、通航枢纽、桥梁等的通航条件进行试验研究。多年来，研究工作者运用船模结合水工或河工模型来研究通航条件问题，优化航道或通航建筑物等的平面设计，在解决重大关键技术性问题中（如三峡工程、葛洲坝工程等）发挥了重要作用，取得了大量的研究成果，研究手段和方法也日趋成熟。实践证明，运用船模结合水流模型来研究通航条件问题，能综合反映水流条件、通航建筑物平面布置的优劣程度，比单纯使用水流模型更科学直观。

目前自航船模仍不完善，如船模试验的测量工具相对于计算机领域的飞速发展相对滞后。同时船舶试验投入的人力物力大，研究周期长。随着水运工程建设步伐的加快，工程项目从立项到建设的时间缩短。特别是在项目前期论证阶段，要求科研的投入少、时间短，物理模型试验这种单一的研究手段已经不能满足市场发展的需要，而数值模拟这种高效实用的研究方法和手段越来越多地应用在水运科研中。

水流泥沙数值模拟已经在国内广泛运用且具有较高水平，但是船舶航行操纵的模拟研究水平及实用性还有待加强。从市场发展情况看，今后船舶航行操纵数值模拟计算也同样具有广泛的应用前景。

1 船舶航行操纵平面二维数学模型的计算模式

目前船舶航行操纵数学模型（以下简称船舶数模）主要分为2类，一类为水动力模型，一类为响应模型。水动力模型具有较完善的水动力结构，不仅能描述船舶本身的性能，还能引进风、浪、流及浅水效应等环境因素，形成船舶—航道—环境系统，可用于研究复杂条件下的船舶航行。目前多数国家的船舶数模均采用了这类模型。船舶操纵性水动力数学模型又分为整体型（以Abkowitz方程为代表）和组合型（以日本M.M.G方程为代表）2大类。一般工程应用组合型比较方便，因此本文基于组合型数学模型预报船舶操纵性能。

虽然航行视距、航道尺度大小、航道等级高低、沿河两岸的景物等对船舶航行和驾驶有一定影响，但水流流场对船舶操纵的影响最大，即航道水流流速的大小、水流方向及流态等是影响船舶操纵的主要因素。所以船舶数模的环境场一般只考虑水流场，即船舶数模包括2个模型：水流数学模型和船舶航行数学模型，其中水流数学模型是船舶航行模拟的基础。

2 平面二维水流数学模型的建立

天然河流中的水流运动多呈三维性，但三维问题较复杂且基本理论很不完善，一般情况下很少采用。河流、湖泊、海岸等的平面尺度一般远大于水深尺度，因此采用沿水深平均的二维水流微分方程来模拟天然水流，不仅经济，同时能较好地反映实际情况。

采用有限体积法建立平面二维水流数学模型［1-2］。有限体积法的基本思想是将计算区域划分成若干个互不重叠的控制体，每个控制体包含一个计算点，然后对每一个控制体积积分，这样便可得到一个包含有一组网格结点处变量值的离散化方程。有限体积法最大的优点是，无论计算网格粗细，离散方程的解均表示了一些物理量（如质量、动量及能量等），在整个计算域内积分守恒可以精确地得到满足［3］。

3 船舶航行操纵数学模型的建立

3.1 船舶航行操纵数学模型的基本原理

基本假设：（1）船舶航行在无限深广水域；（2）自由液面为静水面，船体认为是刚体；（3）忽略船舶纵摇及升沉。

船舶在水中的操作运动，可以看作是船首尾方向及正横方向的并进运动及绕船重心垂直轴的回转运动，即可将船舶运动视为前进、横移和旋回的复合运动。运动和作用力的关系可以用牛顿第二定律来描述。根据图1的坐标系统及受力方式，得到如下方程组

式中：X0为作用于船x0轴方向的合力；Y0为作用于船y0轴方向的合力；N为绕船重心垂直轴的合力矩；m为船的质量；Φ为船的转头角；x0G、y0G为在t0时刻船重心G的坐标；Izz为绕z轴的船的质量惯性矩。其中m为已知量，若力X0、Y0、N已知或可通过其他途径求出，就可以得到船舶的运动轨迹、航速、航带等，进而可分析航道的航行条件。由于船舶运动环境的复杂性，力和力矩X0、Y0、N并无理论解析解，现有方法是通过试验研究成果，建立力与船舶操作运动参数的经验关系式。

从已有的力关系式分析，力的组成分为3个部分，一是航道水流所引起的力，二是船舶操纵引起的力，三是其他外部作用力（如风、浪等）。由此求解船舶运动应首先弄清楚航道水流条件，然后给定操舵、用车等操纵参数，再分析计算船舶所受的作用力，最后在此基础上求解式（1），得到船舶运动过程［4］。

3.2 船舶运动方程

为应用方便，以船体重心G为原点，船首尾为x轴，垂直于船首尾向为y轴（图1），则可得到下式

式中：γ为转艏角速度；u、v为船速V在船首尾方向及横向的分量；mxyZ为x向、y向的附加质量和附加惯性矩［5-6］。

3.2.1 各项水动力表达式

（1）附加质量和附加惯性矩

（2）X、Y、N表达式为

式中各项下标含义为：H为裸船体；P为桨；R为舵；W为风；C为流；F为波浪；S为岸壁。

3.2.2 作用在船体上的水动力表达式

（1）船体纵向水动力

（2）船体横向粘性水动力

（3）船体首摇力矩

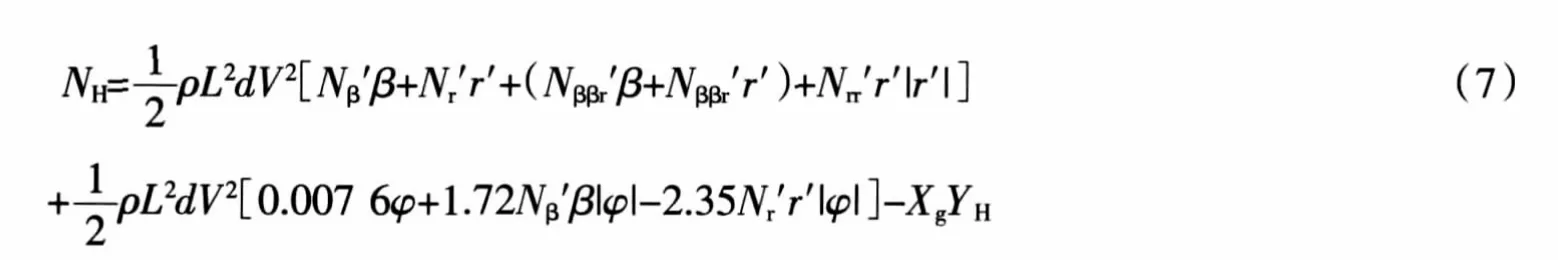
3.2.3 螺旋桨的推力

根据螺旋桨理论，螺旋桨推力XP表示［6］为

式中：t为螺旋桨推力减额；np为螺旋桨转速；DP为螺旋桨直径；JP为进速系数。

3.2.4 舵力及力矩

舵产生的力及力矩包括XR、YR、NR和KR。考虑到单独舵产生的力以及其与船体相互影响产生的附加力，本文采用下列形式［6］

式中：FN为舵的法向力；δ为转舵角（以转右舵为正）；αH为舵与船体水动力影响系数，αH=1.052Cb+0.125；XR、ZR为舵中心处的纵向和垂向坐标；1-tR=0.28Cb+0.55。

（1）舵法向力表示为

（2）舵处的有效来流速度采用芳村公式

（3）舵处的有效攻角，当船舶作曲线运动时，舵处的几何漂角为

3.2.5 其他作用力

（1）风作用力。

式中：ρα为空气密度；Vα为风速；α为风舷角；Af为水线以上船舶正投影面积；As为水线以上船舶侧投影面积；CXα、CYα、CNα为实验系数。

（2）流作用力。

式中：ρ为水密度；Vc为水流速度；α2为水流入射角；Afw为水线以下船舶正投影面积；Asw为水线以下船舶侧投影面积；CX、CY、CN为实验系数。

（3）波浪作用力。

式中：ρ为水密度；g为重力加速度；ξw为平均波浪幅值；θw为波浪方向；ψ为船首向；CXW、CYW、CNW为波浪漂移力系数。

3.2.6 浅水影响

受浅水影响，各项水动力的修正公式表达为

其中各项水动力修正参数f（h）有所不同［4］。

3.2.7 侧壁效应［7-8］

3.3 船舶运动方程的求解

将式（2）离散，则每一时刻船舶的运动可以通过离散方程逐次积分求得。视船舶对岸航速为绝对速度，则船舶对水流的运动为相对运动，对水流速为相对流速，通过对水运动的方程式离散求解，可得对岸运动的参数［4］。

3.3.1 对水运动

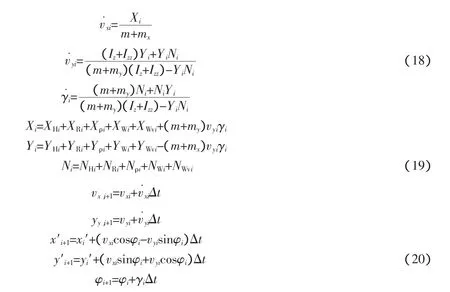
式中：x′、y′为船体重心坐标（对水）；φ 为船摇角；γ 为回转角速度；vx、vy为船对水运动速度在 x、y方向的分量。

3.3.2 对岸运动

在对水运动计算的基础上可进一步计算船对地运动的航行参数。

式中：ux、uy为船对地运动速度在x、y向的分量；vF为流速；ψF为水流流向；x、y为船舶重心对地坐标。

4 船舶航行操纵数学模型的参数率定

为了获取船舶运动的各水动力参数，须对所建立的船舶数模进行参数率定。船舶数模的参数率定在静水、均匀流条件下进行［4，9］。

4.1 船舶静水操纵性率定计算

静水率定采用上海船舶运输科学研究所“5 000 t级、3 000 t级多用途船模型制作和操纵性能率定试验”中的资料。

4.1.1 船舶回转模拟计算

根据实船回转试验资料，分别对3 000 t和5 000 t船进行回转计算，回转计算结果见图2。由图2可知，船舶数模计算结果与实船回转试验结果比较接近。

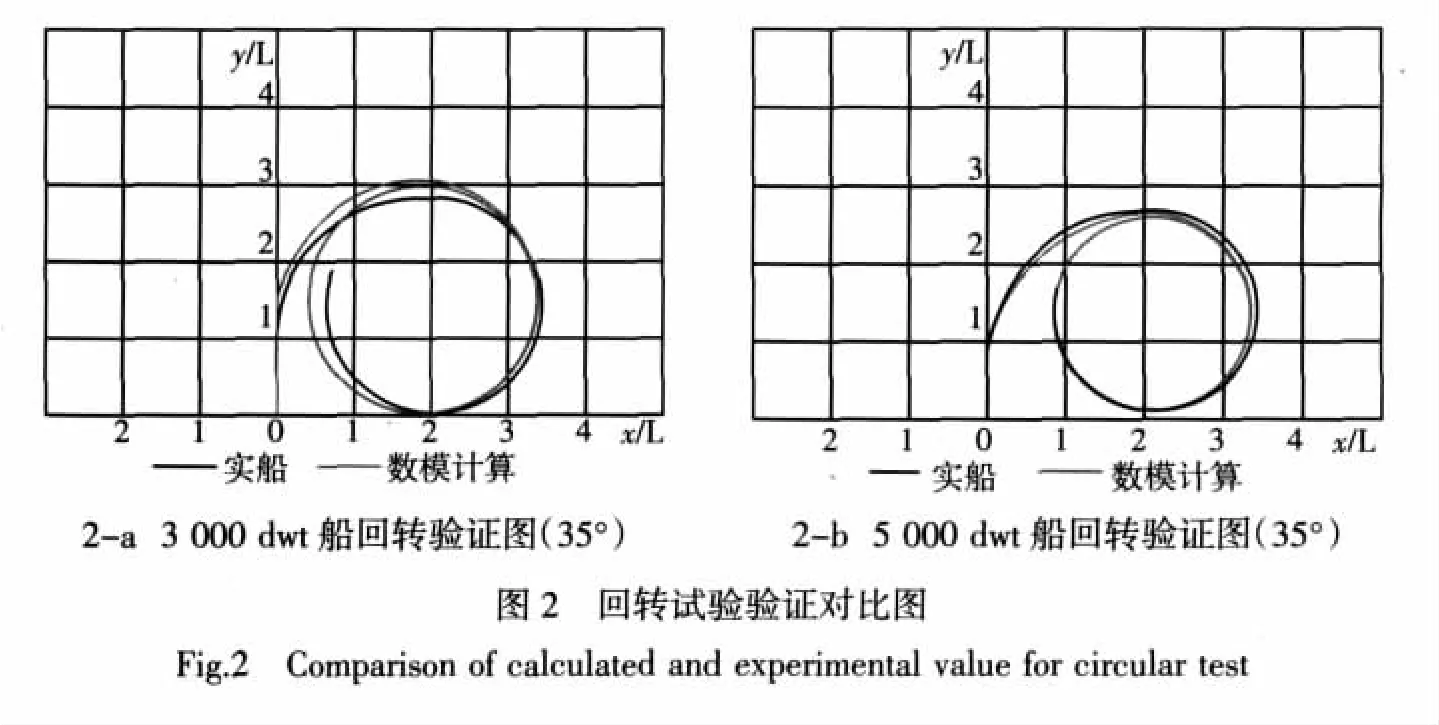
4.1.2 船舶Z形操纵性模拟计算

分别对3 000 t和5 000 t船进行Z形操纵验证计算，计算结果见图3。由图3可知，船舶数模计算结果与船模Z形操纵试验结果比较接近。

4.2 船舶在均匀流中航行操纵性检验计算

4.2.1 基本资料

船舶在均匀流中航行操纵性资料采用交通部天津水运工程科学研究院研究的“上虞新港区闭合式港池船闸口门优化布置试验研究”的船模航行资料。该研究采用自航船模试验的方式，对船闸口门区通航条件进行了研究。因船闸外的地形较为平坦，地形变化不大，流速近似为均匀流，此次均匀流验证计算的内容为船舶在船闸外的航行操纵情况。

4.2.2 检验计算

分别对涨、落潮流速为1.5 m/s、2.0 m/s、2.5 m/s 3种情况进行了计算。由检验计算结果可知，计算值与船模试验值比较接近，个别情况虽存在一定误差，但差值不大。

4.3 船舶数模参数率定小结

由船舶静水回转模拟计算、船舶Z形操纵性模拟计算、船舶在均匀流中航行模拟计算可知，船舶数模的计算结果与实船或船模试验结果比较接近，说明本文建立的船舶数模基本能够反映所模拟船舶的航行操纵性能，可用于下一步船舶在非均匀流中的航行模拟。

5 结语

（1）本文研究开发了船舶航行操纵平面二维数学模型，其中水流数学模型采用贴体坐标系下的平面二维水流数学模型，船舶航行操纵数学模型采用常用的组合型水动力模型。

（2）根据实船或船模在静水条件及均匀流条件下的航行试验资料，对所建立的船舶数模进行了验证和参数率定，结果表明本文建立的船舶数模能够正确模拟船舶的航行操纵性能，具备实用的基本条件。

（3）下阶段应进一步收集天然情况下船舶航行试验资料，对已建立的数学模型进行进一步验证，从而提高船舶数模的计算精度，同时开展工程河段船舶航行操纵数值模拟的研究，以便应用于实际工程。

［1］刘万利.平面二维全沙数学模型研究及其在航道工程中的应用［D］.武汉：武汉大学，2003.

［2］LIU W L，LI Y T，CAO Z X.Two-dimensional Modeling of Alluvial Rivers in Mountain Areas［C］//Proceedings of the 10th International Symposium on River Sedimentation.Moscow：Moscow state university，2007：618-625.

［3］Patankar S V.Numerical Heat Transfer and Fluid Flow［M］.Washington，D.C.：Hemisphere Pub.Co.，1980.

［4］刘万利，张波.内河航道船舶航行操纵平面二维数值模拟初步研究报告［R］.天津：交通部天津水运工程科学研究所，2008.

［5］董国祥.船舶操作性预报仿真及其在船舶初步设计中应用研究［D］.上海：上海交通大学，1996.

［6］苏兴翘.船舶操纵性［M］.北京：国防工业出版社，1981.

［7］Korsmeyer F T.Computation of Ship Interaction Forces and Moments in Resticted Waters［J］.J.S.R.，1993，37（4）：298-306.

［8］Gui Q Y.Computation of Ship Interaction Forces and Moments in Restricted Waterways Using the Numerical Conformal Mapping Method［J］.I.S.P.，1990，37（412）：401-419.

［9］屠海洋.5 000吨级、3 000吨级多用途船模型制作和操纵性能率定试验［R］.上海：上海船舶运输科学研究所，2006.