下降对称的Polak-Ribiere-Polyak共轭梯度法

刘东毅，邵 琛

(1. 天津大学理学院，天津 300072；2. 天津大学电气与自动化工程学院，天津 300072；3. 哈尔滨理工大学应用科学学院，哈尔滨 150080)

不同参数βk对应不同的算法，如常见的Hestenes-Stiefel(HS)算法[1]，Fletcher-Reeves(FR)算法[2]，Polak-Ribiere-Polyak(PRP)算 法[3]和 Dai-Yuan(DY)算法[4]等．共轭梯度法还需要一维搜索，如广泛使用的强Wolfe线性搜索算法，即步长kα满足

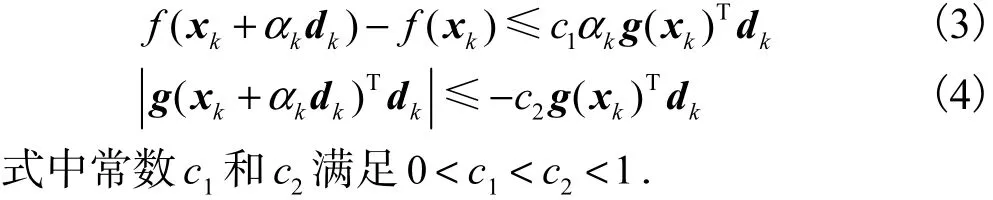
为了保证共轭梯度法的全局收敛性，通常需要搜索方向kd满足下降性质，即

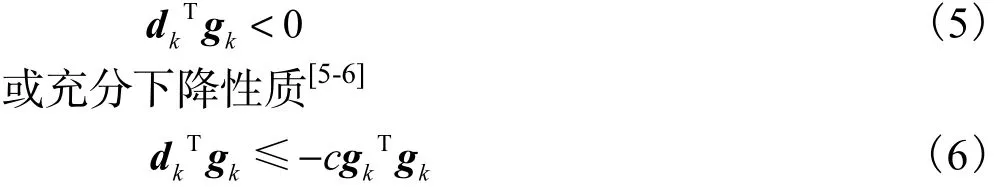
式中： c＞0 ；上标T表示矩阵或向量转置．与拟牛顿法不同，共轭梯度法对于不精确线搜索一般不满足式(5)或式(6)．因此，许多学者致力于研究对于任何线搜索都满足下降性质的算法．Shanno[7]基于 Perry[8]的思想，运用拟牛顿方程和自调比技术，提出了无记忆拟牛顿法和自调比共轭梯度法．Touati-Ahmed和Storey[9]组合了 FR算法和 PRP算法，并提出了一些混合共轭梯度法．Liu和 Storey[10]提出了 LS算法．最近的研究进展参见文献[11-14]．

本文应用对称化技术[15]于 PRP算法，获得一种对称的 PRP算法，它们对于任何线搜索都满足下降性质式(5)和式(6)．更重要的是，这种思想可以应用到其他共轭梯度法中．

1 对称的共轭梯度法

按照 Perry[8]的建议，经典的 HS共轭梯度法[1]的搜索方向1k+d 写成

2 下降对称PRP算法

3 DSPRP算法的全局收敛性

证明 根据 DSPRP算法构造，由式(14)～式(16)可知，它产生的搜索方向1k+d 满足充分下降条件式(6)，再由强Wolfe线性搜索式(3)和式(5)，可得到

4 数值试验

通过一些试验函数来验证DSPRP算法的数值效果，并与PR+算法[6]作比较来说明DSPRP算法的优越性和实用性．试验函数见表1．

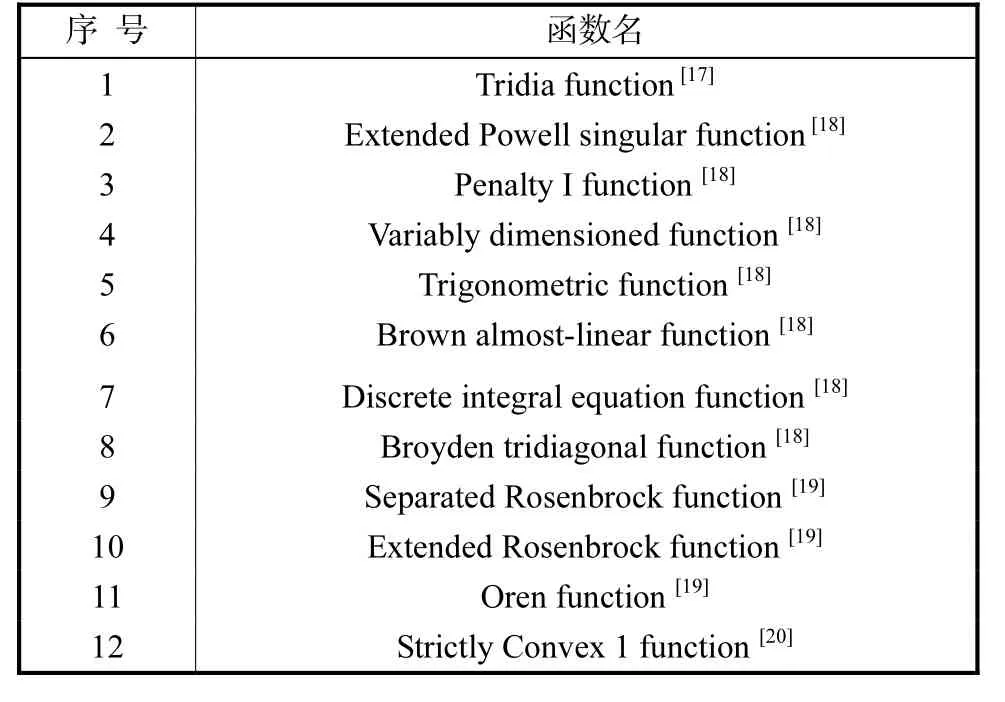
表1 试验函数Tab.1 Test functions

自变量的个数n分别取为1,000和10,000(除函数4与6外)．初始点由文献提供．根据定理3，试验使用强 Wolfe线性搜索，并且其子程序根据文献[16]第3章中的算法编写．记α0,1为线搜索第1次迭代初始试探步长，α0,k+1为线搜索随后的第k+1次迭代初始试探步长．在DSPRP算法中，取γ= 10-4，δ= 1 0-4，μ= 0 .1，σk≡ 1．数值试验分成如下4组．

表2 DSPRP算法的数值结果Tab.2 Numerical results of the DSPRP algorithm

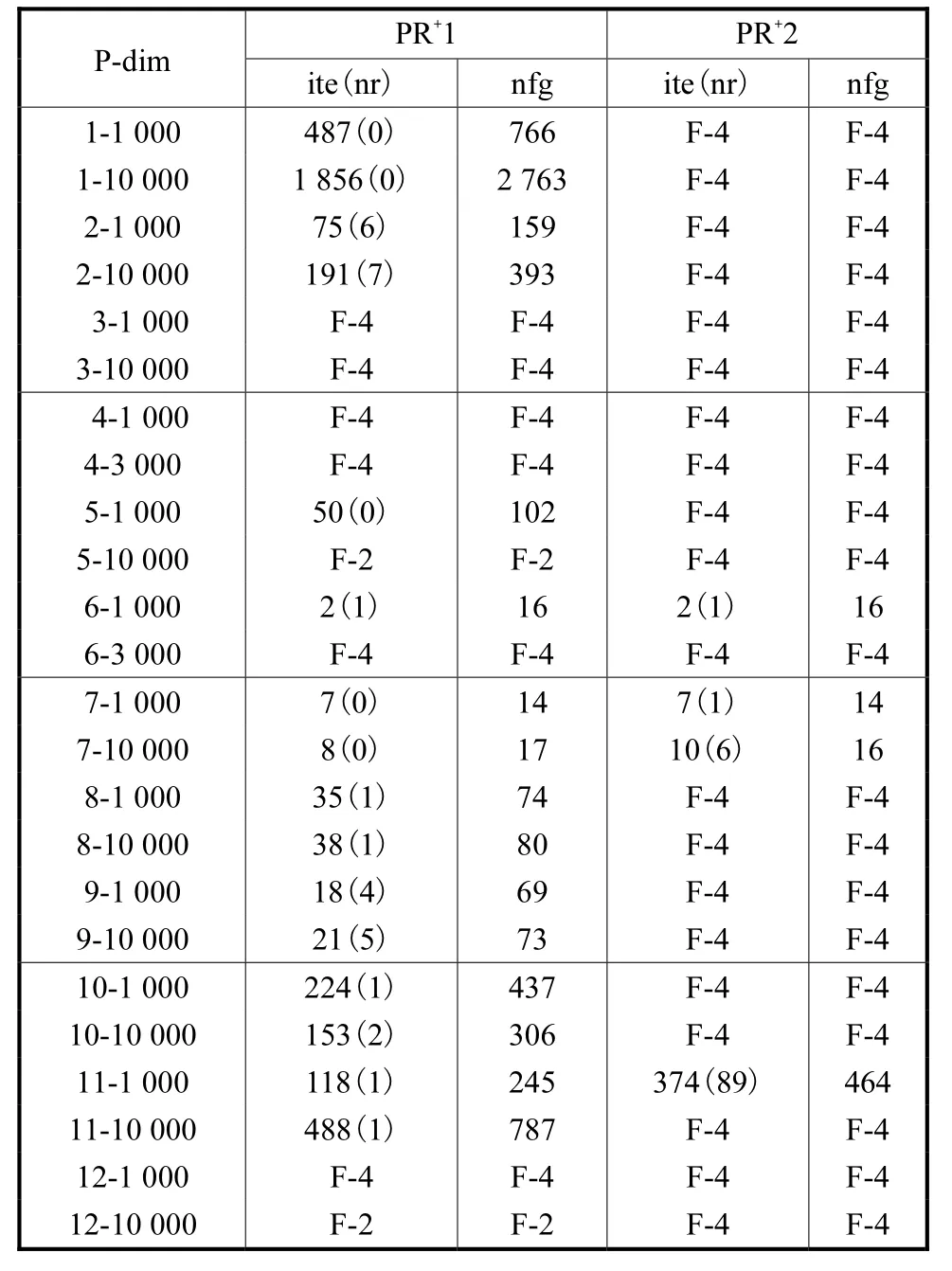
表3 PR+算法的数值结果Tab.3 Numerical results of the PR+ algorithm

从表 2和表 3中可以看出，当线搜比较精确时(20.1c= )，DSPRP算法与 PRP+算法不论从迭代次数还是 nfg的数值上比较，二者的性能均相差不多，但当线搜比较粗糙时(20.9c= )，DSPRP算法要比 PRP+算法的效果好得多．例如：与 PR+1相比，G1和 G2只失败了3次，而PR+1失败了8次；与PR+2相比，G3和G4分别失败了5次和3次，PR+2却失败了20次．因此，可以看出DSPRP算法更实用和稳健．

5 结 语

笔者利用的对称化思想也可以应用到其他共轭梯度法中，如 HS法和 FR法等．在全局收敛性证明中，迭代矩阵谱的分布情况起了很重要的作用，由此得到的收敛性结论是=0．在数值试验中γ和μ的值取得很小，这主要是为了考察对称化的效果，而试验结果正好验证其良好的效果．

［1］Hestenes M R，Stiefel E. Methods of conjugate gradients for solving linear systems [J].Journal of Research of the National Bureau of Standards，1952，49(6)：409-439.

［2］Fletcher R，Reeves C. Function minimization by conjugate gradients [J].Computer Journal，1964，7(2)：149-154.

［3］Polyak B T. The conjugate gradient method in extreme problems [J]. USSRComputation Math and Math Physics，1969，9(4)：94-112.

［4］Dai Yuhong，Yuan Yaxiang. A nonlinear conjugate gradient method with a strong global convergence property[J].SIAM Journal on Optimization，1999，10(1)：177-182.

［5］Al-Baali M. Descent property and global convergence of the Fletcher-Reeves method with inexact line-search [J].IMA Journal of Numerical Analysis，1985，5(1)：121-124.

［6］Gilbert J C，Nocedal J. Global convergence properties of conjugate gradient methods for optimization [J].SIAM Journal on Optimization，1992，2(1)：21-42.

［7］Shanno D F. Conjugate gradient methods with inexact searches [J].Mathematics of Operations Research，1978，3(3)：244-256.

［8］Perry A. A modified conjugate gradient algorithm [J].Operations Research Technical Notes，1978，26(6)：1073-1078.

［9］Touati-Ahmed D，Storey C. Efficient hybrid conjugate gradient techniques [J].Journal of Optimization Theory and Applications，1990，64(2)：379-397.

［10］Liu Y，Storey C. Efficient generalized conjugate gradient algorithms [J].Journal of Optimization Theory andApplications，1991，69(1)：129-137.

［11］Hager W W，Zhang Hongchao. A new conjugate gradient method with guaranteed descent and an efficient line search [J].SIAM Journal on Optimization，2005，16(1)：170-192.

［12］Yu Gaohang，Zhao Yanlin，Wei Zengxin. A descent nonlinear conjugate gradient method for large-scale unconstrained optimization [J].Applied Mathematics and Computation，2007，187(2)：636-643.

［13］Zhang Li，Zhou Weijun，Li Donghui. Global convergence of a modified Fletcher-Reeves conjugate gradient method with Armijo-type line search [J].Numerische Mathematik，2006，104(4)：561-572.

［14］Andrei N. Another hybrid conjugate gradient algorithm for unconstrained optimization [J].Numerical Algorithms，2008，47(2)：143-156.

［15］Powell M J D. A new algorithm for unconstrained optimization [C]//Rosen J B，Mangasarian O L，Ritter K．Nonlinear Programming.New York：Academic Press，1970：31-66.

［16］Nocedal J，Wright S J.Numerical Optimization[M].2nd ed．New York：Springer Science +Business Media，Inc，2006.

［17］Buckley A，Lenir A. QN-like variable storage conjugate gradients[J]．Mathematical Programming，1983，27(2)：155-175.

［18］Moré J J，Garbow B S，Hillstrom K E. Testing unconstrained optimization software [J].ACM Transactions on Mathematical Software，1981，7(1)：17-41.

［19］Grippo L，Lampariello F，Lucidi S A. Truncated Newton method with nonmonotone line search technique for unconstrained optimization [J].Journal of Optimization Theory and Applications，1989，60(3)：401-419.

［20］Raydan M. The Barzilai and Borwein gradient method for the large scale unconstrained minimization problem [J].SIAM Journal on Optimization，1997，7(1)：26-33.