一类Filippov平面系统的闭轨
2010-05-09熊佩英
熊佩英
一类Filippov平面系统的闭轨
熊佩英
(湖南城市学院 数学与计算科学系, 湖南 益阳,413049)
利用微分包含理论和点变换的方法, 对一类Filippov平面系统的滑模解和闭轨的存在性进行了研究, 同时给出了闭轨存在的必要条件.
平面系统;闭轨;微分包含
我们考虑以下平面系统

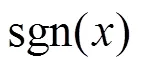
尽管它结构简单却应用广泛, 按我们的知识水平来看, 系统(1)的动力学性质还没有得到完整的研究. 虽然对它的研究已有许多进展, 但存在的结果主要集中在存在性、唯一性、稳定性以及解的渐近性, 很少有关于周期解的结果[1-2, 4]. 对系统(1)的研究最早由 Andronov, Vitt 和 Khaikin在20世纪30年代完成. 在文献[5]中, 作者考虑了具一条不连续相交线的平面系统. 本文将考虑具两条不连续相交线的平面系统:

然后去掉*可得:
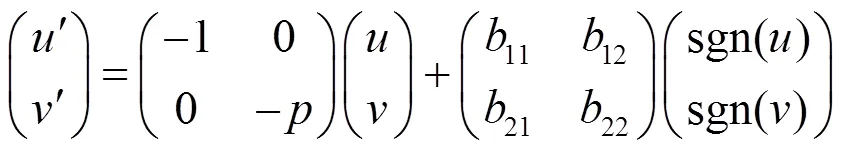

则系统(3)转换成等价系统:

利用微分包含理论, 我们得到以下两个引理.
对于初值问题(5), 我们运用文献[4,p77]中的定理1可得引理2.



自我持续振动出现在许多生物、物理和工程系统中, 在平面系统中出现的自我持续振动是周期振动. 我们将研究系统(4)的周期振动的存在性.
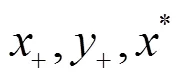

通过计算, 我们得到无滑模运动的闭轨存在的重要结果.

由式(6)得:



因此, 定理1中a成立.
注:由引理1和引理3可知, 系统(4)没有具滑模运动的闭轨.
[1] Bacciotti A, Ceragioli F. Stability and stabilization of discontinuous systems and nonsmooth Lyapunov func- tions[J]. Esaim-Cocv, 1999, 4(2): 361-376.
[2] Forti M, Nistri P. Global convergence of neural networks with discontinuous neuron activations[J], IEEE Trans. Cir- cuits Syst I, 2003, 50: 1421-1435.
[3] Andronov A A, Vitt A A, Khaikin S E. Theory of oscillators[M]. Oxford: Pergamon, 1966: 151, 157, 443- 446, 501.
[4] Filippov A F. Differential equations with discontinuous righthand sides[A]. Mathematics and its Applications (Soviet Series)[C]. Boston, MA: Kluwer Acadmic, 1988.
[5] Giannakopoulos F, Pliete K. Planar systems of piece-wise linear differential equations with a line of discon- tinuity[J]. Nonlinearity, 2001, 14(6): 1611-1632.
Closed trajectory in a class of planar Filippov systems
XIONG Pei-ying
(Department of Mathematics and Computer Science, Hunan City University, Yiyang 413049, China)
Using the theory of differentialinclusions and the method of point transformation, existence of sliding motionsolutions and closed trajectory in a class of planar Filippov systems are investigated. Synchronously, the necessary conditions was given for the existence of closed trajectory.
planar system; closed trajectory; differential inclusion
O 175.12
A
1672-6146(2010)03-0007-02
10.3969/j.issn.1672-6146.2010.03.004
2010-07-06
国家自然科学基金资助(10771055);湖南省教育厅资助(09B019)
熊佩英(1964-), 女, 副教授, 硕士, 主要研究方向为微分方程理论及应用.
