改进的蚁群算法在物流配送路径问题中的实现

郑峰峻（西安建筑科技大学 管理学院，陕西 西安 710055）

配送中心作为物流活动中专职从事配送工作的组织者，具有规模大、配送能力强的特点，从而使得由配送中心对用户进行需求物品配送成为物流配送的主要形式，而其中配送车辆的路径合理与否，对于配送速度、配送费用、运力配备以及配送成本与效益的影响均很大，采用科学合理的方法来确定车辆路径便成为配送中心进行配送活动的一项重要工作。车辆路径问题（Vehicle Routing Problem，VRP）是由G·Dantzig和J·Ramser于1959年首先提出来的，由于该问题具有与实际生活密切联系的特点，吸引了无数学者为之探索，取得了大量的研究成果，如Clark和Wright提出的节约算法、Gillett和Miller提出的Sweep算法、Lin提出的2-opt和3-opt交换算法，以及模拟退火算法、遗传算法、禁忌搜索算法、神经网络算法等。蚁群算法最早是由意大利科学家M·Dorigo于1991年提出，是一种基于群体、用于求解复杂组合优化问题的能用搜索技术，首先被成功应用于TSP问题，随后在一系列诸如二次分配、图着色问题、机器人路径以及通信网络负载等离散优化问题中取得了广泛应用。

蚁群算法独特的空间随机搜索机制、信息素指导机制、信息素挥发机制以及天然的并行特性使得其自身具有广阔的发展前景。本文通过蚁群算法在TSP问题中的应用，给出了求解VRP问题的蚁群算法，取得了较好的效果。

1 蚁群算法简介

1.1 蚁群算法原理

蚁群算法是对自然界蚂蚁的寻径方式进行模拟而得出的一种仿生算法。在蚁群找到食物时，它们总能找到一条从食物到巢穴之间的最优路径。这是因为蚂蚁在寻找路径时会在路径上释放出一种特殊的信息素，当它们碰到一个没有走过的路口时，就随机地挑选一条路径前行，与此同时释放出与路径长度有关的信息素。路径越长，释放的信息素浓度越低，当后来的蚂蚁再次碰到这个路口时，选择信息素较高路径的概率就会相对较大。这样形成了一个正反馈，最优路径上的信息素浓度越来越大，而其它的路径上的信息素会随着时间的流逝而消减，最终整个蚁群会找出最优路径。在整个寻径过程中，虽然单个蚂蚁的选择能力有限，但是通过信息素的作用，整个蚁群之间交换着路径信息，最终找出最优路径。

1.2 蚁群算法的实现

下面以蚁群算法在TSP问题中的应用来对蚁群算法的实现过程进行说明。设m为蚁群的总数；dij表示城市i到城市j的距离；τij表示城市i到城市j之间的信息素量；Δτij表示蚂蚁从城市i到城市j后产生的信息素增量；表示第k只蚂蚁在从城市i向城市j转移时的转移选择概率。

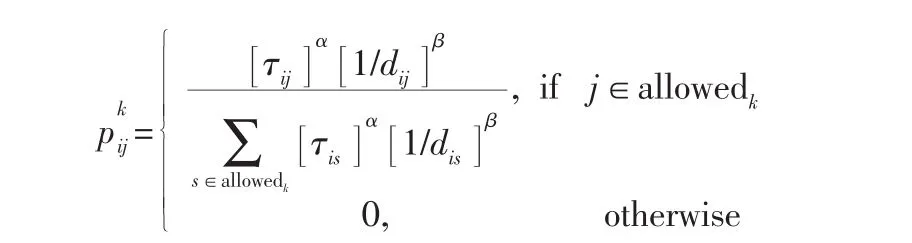
蚂蚁在选择下一个城市时会先计算转移选择概率，allowedk代表第k只蚂蚁尚未访问过的城市；α表示信息启发式因子，它代表在选择路径中信息素的作用程度；β表示期望启发式因子，它代表成本在路径选择中的作用程度。蚂蚁将会选择转移概率最大的城市进行移动。

当一只蚂蚁完成一次遍历后，需要对这只蚂蚁经过的路径进行信息素的更新。在M·Dorigo提出的蚁群算法中提出了三种信息素增量模型，分别是ant-quantity system、ant-density system和ant-cycle system，本文采用的是ant-cycle system模型。

Lk表示第k只蚂蚁在一次遍历中所行走的路径，Q代表蚂蚁所携带的固定的信息素量。在蚂蚁完成一次遍历后，根据下式对局部的信息素量进行更新。

1.3 改进的蚁群算法

由于蚁群算法采用的随机搜索机制，因此在可行解的搜索过程中比较容易达到局部最优解而导致算法停滞的现象。所以在基本的蚁群算法上给出以下几点改进方法，使蚁群算法可以在加快收敛速度的同时保持其搜索路径的随机性，以使算法性能有所提高。

（1）随机化初始位置。初始化蚂蚁位置时，将蚂蚁随机放入各个节点而不是均从一个节点出发，这样有利于搜索路径的多样性，为找到比较好的可行解提供了可能。

（2）信息素设置上下限。由于信息素挥发机制，在一些不常经过的路径上信息素的量会非常小，这样会使算法陷入局部优解的情况，因此算法中引入信息素上限与下限可以增加蚁群搜索路径时的随机性，而不会因为信息素量过小或过大而使算法陷入局部最优。

（3）动态设置期望启发式因子β值。期望启发式因子是计算转移概率时一个很重要的参数，它反映了启发式信息在指导蚁群搜索过程中的相对重要程度。其值越大，则蚂蚁在某个局部点上选择局部最短路径的可能性越大，算法的收敛速度会加快，同时蚁群搜索最优路径的随机性降低，易于陷入局部最优。因此，在算法初期，可以将β值设为比较大的值，这样会加快算法的收敛速度，而在算法进行过程中，通过迭代次数去调整β值，这样可以在保证收敛速度的同时使蚁群在搜索路径时的随机性加大。

2 改进的蚁群算法在VRP中的实现

2.1 VRP问题与TSP问题的区别

从本质上说，TSP[1-3]是VRP[4]的基本问题，也就是VRP问题的一种特殊情况。二者既相似又存在许多的差别，因此在设计求解VRP的蚁群算法时，既要注意吸收用于求解TSP的蚁群算法的经验，又要充分考虑VRP的具体要求。VRP的复杂程度远高于TSP，VRP与TSP的区别主要体现在下面三个方面：

（1）子路径构造过程的区别。在TSP中，每只蚂蚁均要经过所有节点；而在VRP中，每只蚂蚁并不需要遍历所有节点。因此，在求解VRP的每次迭代中，每只蚂蚁移动次数是不确定的，只能将是否已回到原点作为路径构造完成的标志。

（2）Allowedk的区别。Allowedk的确定是蚂蚁构造路径过程中一个十分关键的问题。在TSP中，蚂蚁转移时只需考虑路径距离和信息量；而在VRP中，蚂蚁转移时不但要考虑上述因素，还需考虑车辆容量的限制或者时间窗的限制等。

（3）可行解结构的区别。在TSP中，每只蚂蚁所构造出来的路径均是一个可行解；而在VRP中，每只蚂蚁所构造的回路仅是可行解的“零部件”，各蚂蚁所构造的回路可能能够组合成一些可行解，也可以一个可行解都得不到。因此，研究如何设计算法以尽量避免无可行解现象的出现及如何获取可行解是蚁群算法在VRP领域中应用的关键。

2.2 VRP问题的算法实现

根据上面的分析可以看出在求解VRP问题的可行解与TSP存在着一些不同，下面就VRP的求解给出蚁群算法用于求解VRP问题的伪代码：

Step1：对参数进行初始化。Set信息启发式因子α=1；每条边的信息素量τij=0.1，每条边的信息素增量Δτij=0；将m只蚂蚁随机放到各个客户点上；配送中心车辆的载重量Load=0；设置迭代次数NC=0；将Allowedk的值初始值设置为true即各客户尚未访问，均可以被访问。

Step2：将蚂蚁的初始点放到tabuk中即说明此节点已经被访问，不能再被访问。对于每个蚂蚁k做如下操作：通过转移规则选择下一个访问j，如果这个城市的需求量没有超过车辆的载重量，则选择该客户点j，否则重新选择客户点j。将蚂蚁转移到客户点j，将客户点j放入tabuk中，并将客户点的载重量加入Load中，即：Load=Load+demand[]j；判断Load是否超过车辆的最大载重量，如果未超过则继续选择下一个客户点，否则返回配送中心。

Step3：判断Allowedk中是否还有未访问的客户点，如果还有其它尚未访问的客户点则设置从配送中心出发，跳转到Step2；如果Allowedk中的客户点已全部访问完毕，则第k只蚂蚁完成一次遍历，继续下一步。

Step4：从tabuk中计算第k只蚂蚁的解集中所经过的路径的长度lengthk。

Step5：根据各只蚂蚁经过的路径利用局部信息素更新机制来更新各只蚂蚁所经过的路径的信息素量； Δτij=Q，其中Q代表蚂蚁所产生的信息素增量。

Step6：从m只蚂蚁中所经过的路径长度得出最短路径。

Step7：从每次迭代的最短路径中得出目前最优的路径，然后根据全局信息素更新机制来更新目前最优路径的信息素。

Step8：NC++；根据迭代次数动态更新期望启发式因子β值。

Step9：当NC＞NCmax即迭代次数超过设置的最大迭代次数时，输出可行解。

3 算例分析

为了检验算法的有效性，本文从国际上公认的VRPLIB问题库中选取了两个（eil30和eil22）进行了算例检验，得到了比较满意的结果如图1、图2所示。

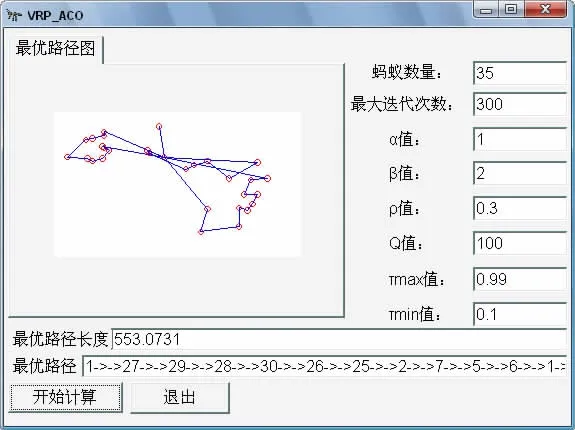
图1 Eil30仿真结果

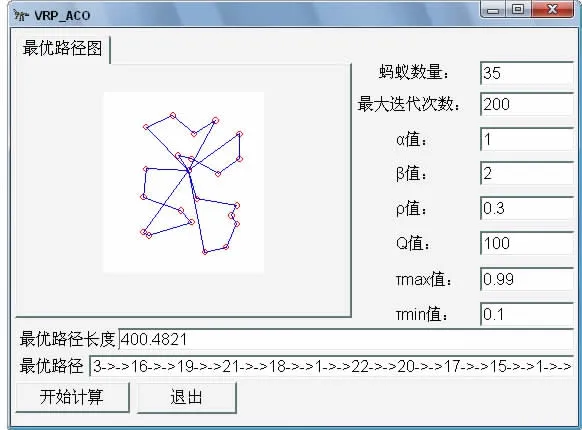
图2 Eil22仿真结果

Eil30容量限制为4 500，最优配送路径的长度为：553.0731。

路径分别为：1->->27->->29->->28->->30->->26->->25->->2->->7->->5->->6->->1；

1->->3->->4->->23->->21->->20->->19->->24->->1；

1->->13->->12->->11->->16->->17->->14->->8->->18->->10->->9->->15->->1；

1->->22->->1。

Eil22容量限制为6 000，最优配送路径的长度为：400.4821。

路径分别为：1->->14->->12->->9->->7->->5->->4->->1；

1->->2->->3->->6->->8->->10->->11->->1；

1->->13->->16->->19->->21->->18->->1；

1->->22->->20->->17->->15->->1。

4 结 论

在物流配送系统中，合理安排车辆路径是减少浪费、提高经济效益的重要手段，然而由于问题本身的NP完全的性质，精确求解非常困难，启发式算法不失为一种可行的方向。本文通过蚁群算法在TSP中的应用，分析TSP与VRP的异同，给出求解VRP问题的蚁群算法，并对蚁群算法存在的过早收敛问题，通过随机化初始位置、信息素设置上下限以及动态设置期望启发式因子β值三种措施，对求解VRP问题的蚁群算法进行改进，最后由powerbuilder仿真实验对算法进行实现并得出了比较满意的结果。

[1]毕军，付梦印，张宇河.一种改进的蚁群算法求解最短路径问题[J].计算机工程与应用，2003,39(3):107-109.

[2]储理才.基于MATLAB的遗传算法设计及TSP问题求解[J].集美大学学报，2001(3):14-19.

[3]赵学峰.一种求解TSP的混合蚁群算法[J].西北师范大学学报，2003,39(4):31-34.

[4]刘云忠，宣慧玉.蚂蚁算法在车辆路径问题中的研究[J].信息与控制，2004,33(2):249-252.