基于有限元分析的实腹式石拱桥合理计算模式研究

魏召兰，蒲黔辉，施 洲

(西南交通大学 土木工程学院，成都 610031)

石拱桥，在我国有着悠久的历史，许多建于20世纪60年代的拱桥目前仍在正常运营。这意味着依据旧规范设计的拱桥承担着新规范规定的增大设计荷载，使拱桥的安全性相对降低。要确定既有桥梁的实际工作状态，必须进行详细的检测与评定。

现有桥梁评估的方法众多，各方法之间存在着一定的区别和联系。目前，既有桥梁承载能力的评估方法主要有:基于外观调查评定法、荷载试验法、承载能力的计算机有限元模拟等几种方法。基于外观调查评定法往往与检查人员的经验和知识密切相关，主观性强，不同评定者有可能得出不同的结论甚至截然相反。荷载试验法通过现场荷载试验可获得部分桥梁结构的确定信息，从而降低桥梁评估中的不确定性，对具体桥梁结构而言，更加准确可靠，但成本较高。承载能力的计算机有限元模拟是以有限元数值分析方法建立详细的桥梁结构的全桥或局部有限元模型，并根据实测损伤结果对桥梁结构的受力作详细的分析，计算结果与相关评估规范结合用以评定结构的承载能力。

目前，一种较为合理的做法是建立符合实际的有限元计算分析模型，并与实桥病害调查及荷载试验结合起来对桥梁承载力进行评估。通过有限元方法对桥梁进行分析和研究已经成为桥梁性能评定的必要手段之一，国内外部分学者也进行了相关研究［1-5］。周岑等［1］对丹河特大跨径石拱桥进行了全桥结构仿真分析研究，从施工过程及成桥阶段、拱上建筑的联合作用、动力特性的角度进行了研究，得到了较为可信的结论。Paul等［5］建立了改进精度的三维有限元模型来模拟爱尔兰都柏林格里菲思桥，并与实桥试验进行了对比分析，得到了很吻合的结果。

本文利用平面有限元分析软件建立老旧实腹式石拱桥较为符合实际的模型，研究出较为合理的内力值方法。结合某中小跨径实腹式石拱桥的详细检测试验项目，从影响承载力的因素着手，对其计算模型进行了合理的修正，分析了其方法的可行性，对同类桥梁用有限元数值模拟提供了参考。

1 石拱桥合理评估计算模型的建立

1.1 材料参数取值

1)材料的线弹性模量

由于石材为非均匀不连续材料，对于其弹性模量目前还没有比较准确的测试手段，一般是根据文献［7］的有关规定取值。规范的弹性模量取值与石拱结构的实际弹性模量差异较大，并且石拱结构的应力—应变关系不明显，导致实际测量值与计算值差别较大。因此石拱桥砌体结构弹性模量的测定是石拱桥承载能力检定工作的重要环节。

石拱桥砌体结构在受压状态下发生的变形主要是砂浆变形引起的，因为石料的弹性模量和强度相对于砂浆的弹性模量和强度要大很多。因此，石拱桥砌体的弹性模量主要取决于砂浆的强度等级(弹性模量)。但国内石拱桥施工过程中很少有砂浆弹性模量的试验数据，这给石拱桥承载能力的检定和维修加固工作带来了很大的困难。聂建国在文献［7］中提出，根据现场静载试验的结果来调整有限元模型的弹性模量参数，使活载下的跨中挠度实测值与计算值相一致，故建议在类似结构分析中，石材的弹性模量取为5.0 GPa。本文石材的弹性模量参照文献［7］的取值。

2)材料强度

有限元分析往往将结构简化为均匀连续体进行计算，一定程度上与石拱结构的实际特性有所不同。石料的抗压强度设计值和砌体的抗压强度设计值不同，当进行验算和设计时以砌体抗压强度设计值为准。

在桥跨结构材料的强度检测中，石料强度按相应的钻芯取样规程并由试验测得。根据实测石料强度，参照文献［6］的有关规定，并结合石拱桥砌筑的实际情况，对砌体抗压强度、弯曲抗拉强度等进行取值。

1.2 拱轴线的选取

拱轴线形与拱圈截面的受力密切相关。由于施工技术水平的差异或后期变形所致，拱轴线并不是很标准，拱圈也不完全对称。这样的拱轴线型在一定程度上影响拱桥的整体受力，使得拱圈长期处于不良的受力状态，影响拱桥的使用寿命，并造成不同程度的拱圈损伤。拱轴线变形会使拱轴线与恒载压力线的偏离加大，而在拱中产生较大的附加内力，从而影响拱桥的承载力。对拱桥实际工作状态的评定，应将实测拱轴线形与设计线形进行比对，若有差异，分析其原因，从而选择符合实际的拱轴线形进行建模计算。

1.3 恒载、活载的计算模式

选用专用平面有限元程序建立裸拱有限元模型进行分析，对于老旧石拱桥，结合其施工过程，为更好地模拟裸拱的实际受力，将一期恒载与活载、二期恒载等作用分别建模计算，再根据相关规范评定其承载能力。

1.3.1 一期恒载作用的计算模式

老旧中小跨径石拱桥，拱圈采用满堂支架，一次落架连续砌筑完成，拱脚处的弯矩很小，可忽略不计，故对一期恒载(自重等)可简化成拱脚为铰接的模式进行计算。

1.3.2 活载、二期恒载等作用的计算模式

拱圈达到相应的强度后，其边界条件发生了变化，此时应按设计要求的边界条件进行计算。对于活载，主要指车辆荷载，以集中力模拟其轴重直接施加于裸拱上时，对个别截面很不利，而且也与实际受力状况不符，主要原因在于裸拱上拱上填料对拱桥的性能有很大影响，可通过扩散作用减少活载作用于拱圈的集中力。故模拟活载作用时，考虑填土的扩散作用，将轴重等效为均布荷载施加在裸拱上，从而使计算得到的截面活载内力更为符合实际情况。

模拟活载作用的具体方法是，根据控制截面(左右拱脚、L/4、L/2、3L/4截面，L为计算跨径)的弯矩影响线，将设计荷载(重车)以考虑填土扩散作用后的均布荷载方式进行加载，以获得控制截面的最大弯矩和最小弯矩。老旧石拱桥拱背填料的准确性能很难被准确掌握，而且其力学性能差异较大，本文根据记录和对填料的观察，并结合相应规范，考虑填土对车辆荷载的影响时，以45°角进行扩散，从而换算成均布荷载q=P/l施加于结构中，具体见图1所示。

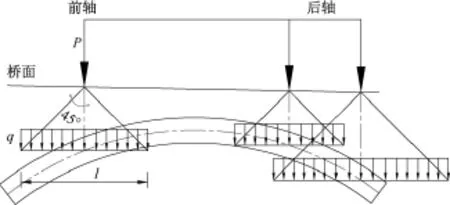
图1 考虑填土扩散作用示意

对于拱上作用的拱上填料、侧墙、桥面铺装等二期恒载按线性荷载施加在裸拱上。

2 基于有限元模拟的承载能力检算原理

目前在建立有限元模型分析后，进行承载力检算时一般是基于现有桥梁相关评估规范。在建立较为符合实际的有限元模型后，根据文献［8-9］中规定对计算分析结果进行组合。根据组合结果，对石拱桥进行主拱圈砌体截面强度验算。但由于桥梁构件的病害及缺损将改变结构受力图式，导致结构的内力重分配，这点在有限元模型中并未充分体现。故在考虑结构退化后的受力行为，即病害及结构缺损对承载力的折减处理方法时，仍采用引用修正系数的方式对计算结果进行折减，按下式进行计算［10］:

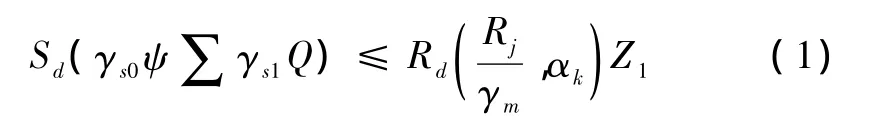
式中，Sd为荷载效应函数;Q为荷载在结构上产生的效应;γs0为结构的重要性系数;γs1为荷载安全系数;ψ为荷载组合系数;Rd为结构抗力效应函数;Rj为材料或砌体的极限强度;γm为材料或砌体的安全系数;αk为结构的几何尺寸;Z1为结构承载能力检算系数，它是通过现场调查，根据实际结构的损伤情况(如开裂、结构破损等)，由鉴定专家根据经验给出的调整系数，文献［10］根据桥梁的类型和桥梁现状给出了取值范围。

若进行了荷载试验，则由试验时结构挠度值和计算挠度值进行比较，获得结构校验系数η，再将η换算为旧桥验算系数Z2，从而用于对所评估石拱桥结构的承载能力进行折减。则式(2)为

式(2)中的符号意义同式(1)。文献［10］也提供了由η确定出Z2值的相应表格。

3 工程实例分析

3.1 工程简介

四川广元市某大跨圬工拱桥位于朝天镇北端跨越潜溪河该桥全长123.65 m，共4孔，孔径布置为(10+85+2×10)m。主桥主跨为空腹式悬链线块石肋拱，净跨85 m，每肋宽2 m，两肋中距5 m，净距3 m，两肋拱之间设置14根钢筋混凝土横系梁。引桥大滩侧2孔，朝天侧1孔，均为净跨10 m的实腹式块石板拱。设计荷载汽—20，挂—100。本文以朝天侧1孔引桥为研究背景。为了判定其目前的实际状况，对该引桥进行了详细的检测及荷载试验，并按照前述方法建模方式分析其承载能力。

3.2 实桥现场调查及静载试验结果［11］

1)石料强度检测。钻芯取样后由试验测得石料的标准抗压强度为65.7 MPa，满足强度设计要求。

2)病害检测。拱圈底面周边渗水钙化严重，且有与硬物擦挂的痕迹，砌缝较宽，约为2～4 cm，拱脚中部存在1条横向裂缝，裂缝长度100 cm，宽度为0.5 mm;其它部位无明显裂缝。

3)实测拱轴线与设计拱轴线比较。实测拱轴线与设计拱轴线走向见图2所示，拱圈测点高程的实测值与设计值的差值在－3.6～6.7 cm之间，两者相符较好。拱圈各测点的水平坐标的偏差也很小。拱轴线的测试结果表明，桥跨结构的几何线形良好，无明显变位。

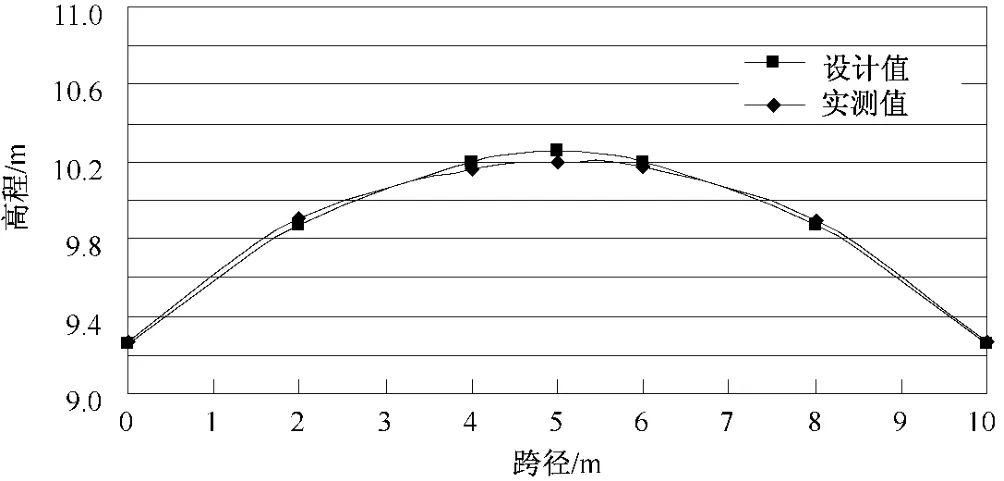
图2 拱轴线形实测值与设计值比较

4)静载试验结果。静载试验的测试内容主要有应力测试和挠度测试，即测试主拱圈各试验截面的应力，以及测试加载跨 L/4、拱顶和3L/4截面的挠度。本桥主要针对拱脚、L/4、拱顶截面做等效加载试验。加载位置主要根据设计控制荷载在主拱圈控制截面上产生的最不利弯矩效应值确定，按0.80～1.05的效率系数等效换算而得。加载过程中采用分级加载，以保证结构的安全。

试验结果表明，各工况下测试截面处的应力、挠度回零情况良好，说明桥跨结构处于弹性工作状态。应力结构校验系数介于0.67～0.78之间，挠度校验系数介于0.54～0.79之间，校验系数分布均匀，均在合理范围之内，表明主拱结构具有足够的强度和刚度。且非加载位置处的校验系数相对于加载位置附近的较大，主要是拱圈上的填料对加载车辆轮压的扩散作用。

3.3 基于有限元模拟的承载能力评估

参照文献［7］的取值，本例材料的弹性模量取为5.0 GPa，强度参数由实测钻芯取样并参照文献［7］取值。以实测拱轴线形选用专用平面有限元程序，建立裸拱模型进行分析。恒载、活载的计算模式按前述原理分开计算，再根据规范进行组合。

拱的截面强度验算应在各受力不利的截面进行，故只将左右拱脚、L/4、L/2、3L/4截面验算结果列出。主拱圈截面强度验算结果见表1。

［10］表4.2，对于不同的检算截面，由不同加载程序得出的校验系数η确定出Z2。当计入承载能力检算系数Z2时，对表1中的抗力RN进行修正，实际抗力R′N如表2所示。

3.4 综合评定结论

采用恒载、活载分开计算的模式，且模拟活载作用时，考虑填土的扩散作用，将轴重等效为均布荷载施加在裸拱上。用此种简化的计算模式进行承载能力评定得出的结果与荷载试验测试结果符合较好。荷载试验表明，挠度校验系数与应力校验系数均在合理范围之内，表明主拱结构具有足够的强度和刚度，能满足设计荷载的承载能力要求。基于简化的计算模式进行承载能力评定得出的结果，即从表2修正后的计算结果也可以看出该石拱桥有一定的安全储备，也能满足设计荷载的承载能力要求，故本文合理评估计算模型的建立具有工程实用性。

4 结语

1)对中小跨径实腹式老旧石拱桥采用平面有限元分析程序进行承载能力评定时，宜在建立较为符合实际的计算模型的基础上。计算模型应考虑桥梁结构的实际施工过程及其病害特点，并从填土对车辆荷载的扩散作用、拱上建筑对承载能力的影响和桥梁结构的缺损造成的受力变化来考虑对模型修正。

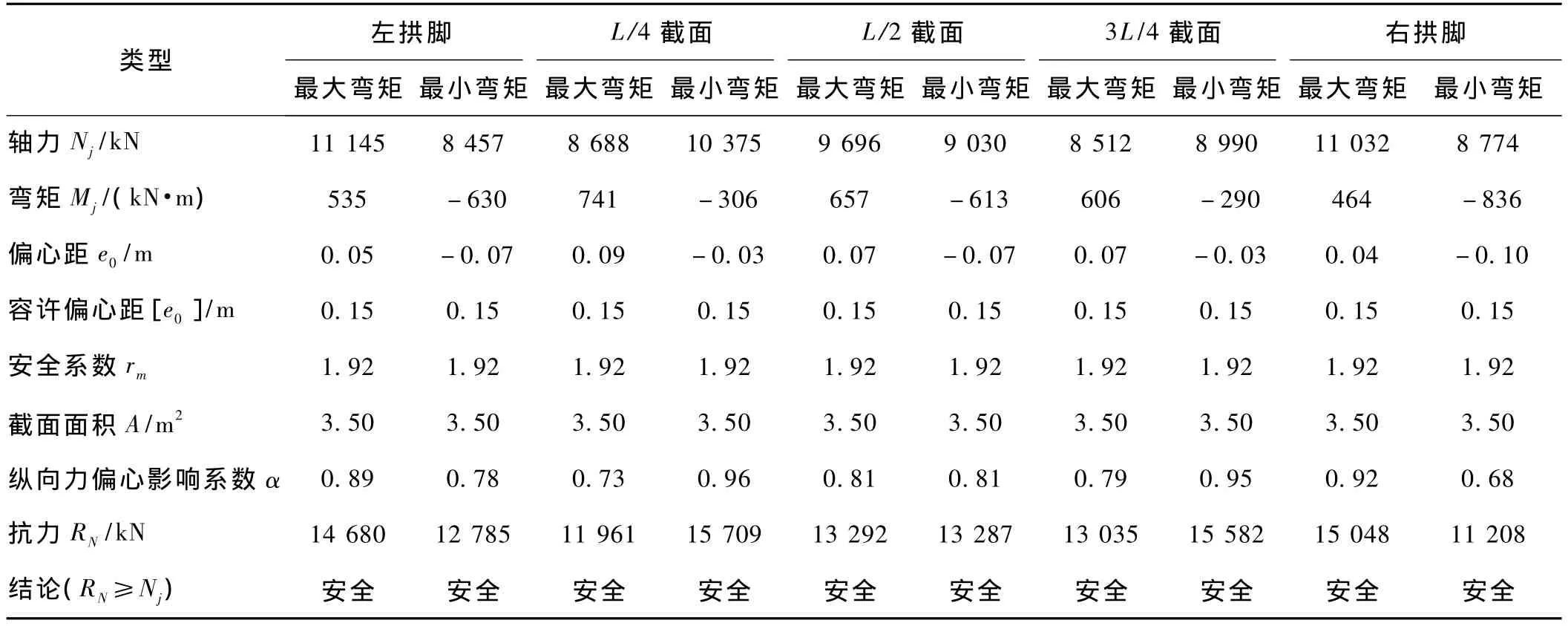
表1 主拱圈强度验算

表2 计入承载能力检算系数时截面抗力

2)文中由荷载试验得出的校验系数η来确定承载能力检算系数Z2，这本身有一定的局限性，宜从拱上建筑、主拱圈自身状况等综合因素建立石拱桥的技术状态评估模型，从而建立一套较为科学的、定量的评价体系及详细的技术评定标准来确定Z2。

3)工程实例证明，基于本文提出的计算模式，计算结果对承载能力鉴定与荷载试验结果符合较好。故可认为此种计算模式较为合理，符合实际情况，具有较好的工程实用性，可适用于同类桥梁结构。

参考文献

［1］周岑，郑凯锋，范立础.大跨度石拱桥的全桥结构仿真分析研究［J］.土木工程学报，2004，37(3):89-92.

［2］葛素梅，陈淮，董建华.双曲拱桥承载能力评估［J］.河南科学，2004，22(1):108-111.

［3］施洲，赵人达.双曲拱桥性能的综合评定及加固方法［J］.公路，2005(9):11-15.

［4］林阳子，黄侨，任远，等.既有石板拱桥的评估及鉴定方法研究［J］.公路交通科技，2008，25(4):89-93.

［5］PAUL J FANNING，THOMAS E BOOTHBY.Three-dimensional Modelling and Full-scale Testing of Stone Arch Bridges［J］.Computers and Structures 2001(79):2645-2662.

［6］中华人民共和国交通部.JTJ022—85 公路砖石及混凝土桥涵设计规范［S］.北京:人民交通出版社，1985.

［7］聂建国，樊健生.700年石拱桥的静力加载试验与结构分析［J］.清华大学学报(自然科学版)，2003，43(6):840-843.

［8］中华人民共和国交通部.JTJ 021—85 公路桥涵设计通用规范［S］.北京:人民交通出版社，1985.

［9］中华人民共和国交通部.JTJ 023—85 公路钢筋混凝土及预应力桥涵设计规范［S］.北京:人民交通出版社，1985.

［10］中华人民共和国交通部.公路旧桥承载能力鉴定方法(试行)［S］.北京:人民交通出版社，1988.

［11］西南交通大学结构工程试验中心.朝天区铁厂河大桥检测评定报告［R］.成都:西南交通大学结构工程试验中心，2009.