基于洪水淹没频率与渠道超高变化的梯形断面明渠优化设计

[印度] R.K.巴他卡利亚 M.萨蒂什

董耀华 译自美刊《灌溉与排水工程》2008年第5-6期

采用优化函数进行明渠断面优化设计是水力学与水资源研究者十分关注的课题,达斯(Das,2007年)提出了一种工程造价与洪水淹没频率最小化的梯形断面明渠多目标优化模型,给出了渠道超高固定情形下表述工程造价与洪水淹没频率之间关系的帕雷托(Pareto)最优化解。依据达斯模型,要使洪水淹没频率较小,渠道顶宽就必须很大。然而随着渠顶宽度的增加,土地成本也会增加,超宽渠道可能会因为占地多而不宜建造,因此,渠顶宽度受到场地适用性与经济可行性等因素的制约。

本文将渠道超高视为附加的设计变量,提出了一种改进的梯形断面明渠多目标优化模型,模型在减少渠道顶宽和降低工程造价等方面比达斯模型更加优越。首先采用传统优化算法求解本文改进的模型,并通过与达斯模型成果比较,评估其优劣。

传统优化算法求解多目标优化问题存在较大的局限性,大部分传统多目标优化算法先将多目标问题转换为单目标问题,再使用单目标传统优化算法求解,一次求解只能得到一个最优解,要想得到全部的帕雷托最优解,必须进行重复计算。但是,如果采用多目标遗传算法,一次求解就能够得到全部的帕雷托最优解,因此,本文最后采用非受控排序遗传算法(NSGA-Ⅱ)给出了改进模型的帕雷托最优解,并与传统优化算法的计算成果进行了比较,以检验NSGA-Ⅱ的适用性。

1 模型的公式表达

如图 1所示,假定明渠梯形断面边坡为 z1和z2,底宽、水深和渠道超高分别为 b、y和 f,渠道两侧和渠底糙率不同,其曼宁系数分别为 n1、n2和 n3,明渠复合断面的等效糙率采用霍顿法(Horton,1933年)计算得出。

图1 明渠梯形断面

渠道优化设计的主要目标是降低工程造价,同时必须使渠道洪水淹没频率最小,以防洪水漫出渠道。为此,达斯提出了如下明渠多目标优化模型:

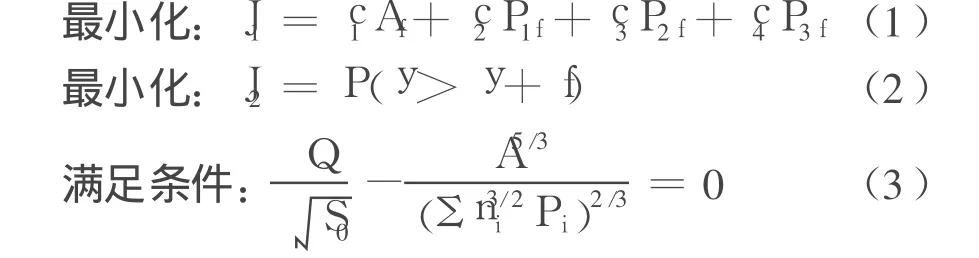
式中 Af为断面总面积;c1为断面单位面积造价;c2为湿周 P1f单位长度造价;c3为湿周 P2f单位长度造价;c4为湿周 P3f单位长度造价;Q为设计流量;S0为渠底纵坡;A为断面过流面积;Pi为湿周长度(i=1,2,3);ni为曼宁系数(i=1,2,3);P(y＞y+f)为水深超过渠道堤顶的频率,根据达斯模型计算。

目标函数 1(式(1))与目标函数 2(式(2))之间存在某种折衷关系,洪水淹没频率越小,渠道工程造价越高;反之,洪水淹没频率越大,渠道工程造价越低。达斯提出了渠道超高固定情形下多目标优化模型的求解方法,并给出了复合糙率、均匀糙率渠道断面的计算结果(表 1)。

由表 1可知,对应于洪水淹没频率极小的渠道断面参数极不合理,例如当设计流量 100m3/s、洪水淹没频率0.01时,达斯模型计算的复合糙率渠道断面设计参数为:渠顶宽度94.26 m、水深0.60m、边坡0.46和0.56。得出的渠道断面很不现实,渠顶宽度太大、实际难以实施。针对这一情况,本文提出了将渠道超高作为附加变量的优化模型,模型变量由此增加为 b、y、z1、z2和 f,模型根据洪水淹没频率确定不发生漫顶时的渠道超高。当洪水淹没频率较小时,渠道超高较大;而当洪水淹没频率较大时,可能不需要渠道超高,因此有必要增加一个最小渠道超高的附加限制条件:

式中 fmin为最小渠道超高。

2 采用传统优化算法求解

综合目标函数式(1)、(2)与限制条件式(3)、(4),构成了本文改进的梯形断面明渠多目标优化模型。首先采用传统优化算法进行模型求解,通过引入 ε-约束,将多目标问题转换成单目标问题,转换后的单目标优化问题可用数学公式进行表达。

最小化:

满足条件:

可采用传统的单一目标优化算法求解上述不同ε值时的单目标优化问题,具体可使用 MATLAB软件的序列二次规划程序求解。

2.1 复合糙率渠道断面的最优解

本文首先对达斯模型复合糙率渠道断面算例进行对比计算,以证明本文模型的优越性。计算参数为:明渠设计流量 100m3/s,其他参数均值分别为c1=0.50、c2=0.30、c3=0.35、c4=0.40、n1=0.030、n2=0.025、n3=0.020和 S0=0.0025,部分参数可随机上浮至 n1=0.033、n2=0.028、n3=0.023、S0=0.0028和 Q=120m3/s(分别浮动 30%、25%、20%、30%和 35%),洪水淹没频率计算使用达斯模型方法。

图2给出了达斯模型与本文模型的帕雷托最优解,由图可知:本文模型的非受控最优解优于达斯模型,展示了模型的优越性。表 1给出了本文模型与达斯模型的最优解,由表可知:当洪水淹没频率为0.01、设计流量 100m3/s和渠道超高可变时,本文模型计算的渠道断面设计参数分别为渠道顶宽10.81m、水深 2.70m、边坡 0.10和 0.11、渠道超高2.47 m、工程造价37.17货币单位;而通过达斯模型得到的渠道超高固定时,相应的渠道断面设计参数分别为渠道顶宽94.26m、水深0.60m、边坡0.46和0.56、工程造价90.73货币单位。达斯模型的渠道断面尺寸很不现实,因而难以实施,而且其工程造价是本文模型的2.44倍。

2.2 均匀糙率渠道断面的最优解

本文对达斯模型均匀糙率渠道断面算例也进行了对比计算,以再次检验本文模型的性能。明渠设计流量 100m3/s,其他参数均值分别为 c1=0.50、c2=c3=c4=0.30、n1=n2=n3=0.030和 S0=0.0025,部分参数可随机上浮至 n1=n2=n3=0.033、S0=0.0028和 Q=120m3/s(分 别浮动30%、30%和 35%),洪水淹没频率计算仍然使用达斯模型方法。

表1 复合糙率渠道断面帕雷托最优解比较

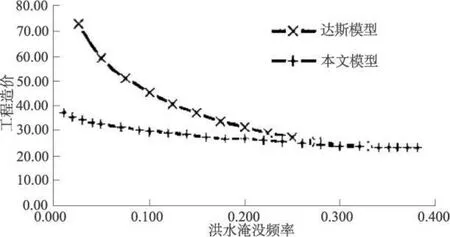
图2 达斯模型与本文模型得出的复合糙率渠道断面帕雷托最优解的比较

图3给出了达斯模型与本文模型的帕雷托最优解,再次表明:本文模型的非受控优化解优于达斯模型。

图3 达斯模型与本文模型得出的均匀糙率渠道断面帕雷托最优解的比较

2.3 顶宽受限渠道断面的最优解

受施工场地的约束,某些渠道的顶宽受到限制,因此,需要在上述明渠非线性优化模型中引入渠道顶宽取值的附加限制条件:

式中 Tf为渠道顶宽;Tmax为最大允许渠道顶宽,本文研究中取Tmax=8.00m。

仍然选取复合糙率渠道断面算例,加入渠道顶宽8.00m限制条件,图 4给出了顶宽受限渠道断面的帕雷托最优解。应指出的是,当洪水淹没频率较小时,达斯模型无法获得该算例的合理最优解,其原因在于:对应于较小的洪水淹没频率,达斯模型会求解出一个超常的渠顶宽度。

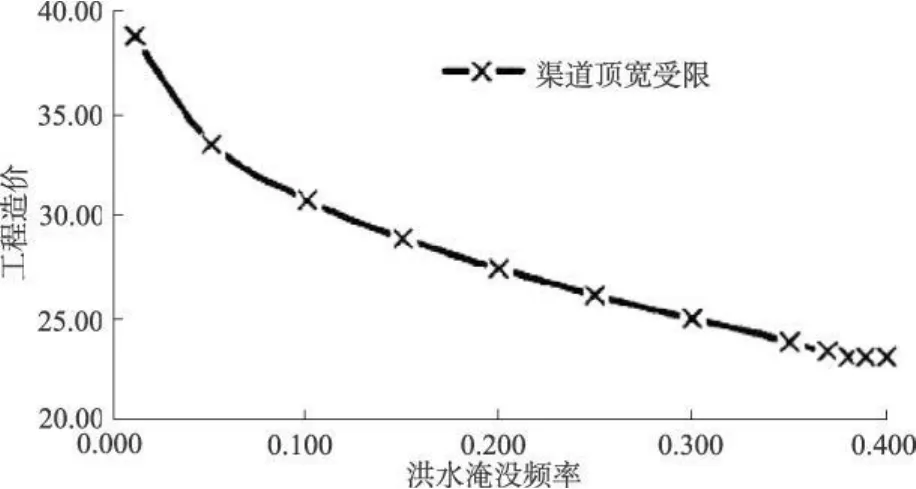
图4 顶宽受限复合糙率渠道断面帕雷托最优解

3 采用非受控排序遗传算法(NSGA-Ⅱ)求解

NSGA-Ⅱ是求解多目标优化问题最佳算法之一,它采用迫使非受控解向帕雷托最优解方向特殊生成的方法搜索帕雷托最优解,并通过“密集间距判据”保持帕雷托最优解的多样性。图 5给出了复合糙率渠道断面的 NSGA-Ⅱ与传统优化算法的帕雷托最优解。采用 NSGA-Ⅱ只需求解一次就可获得所有的非受控最优解,而采用传统优化算法则需要多次求解才能得到所有最优解,两种算法的最优解十分接近。评估结果表明:采用 NSGA-Ⅱ求解渠道工程造价与洪水淹没频率的帕雷托最优解是可行的。

图5 NSGA-Ⅱ与传统优化算法计算复合糙率渠道断面帕雷托最优解的比较

4 结 语

基于渠道超高可变,本文提出了一种新的明渠断面设计优化模型,采用传统优化算法与 NSGA-Ⅱ对本文多目标优化模型进行了求解,并将模型实际应用于梯形断面明渠的优化设计。与以往达斯模型成果进行了对比分析,结果表明:①本文模型在减少渠道顶宽和降低工程造价等方面成效显著;②采用 NSGA-Ⅱ进行本文模型求解是十分有效的。