满速率满分集优化的单频网发射信号

沈 莹，唐友喜

(电子科技大学通信抗干扰技术国家级重点实验室 成都 610054)

在单频网中，分布在不同地理位置的各个发射天线，同时在相同的频率发射相同的信号。与传统的单天线系统相比，单频网具有覆盖更均匀、接收更可靠和易于扩展等特点[1-3]。单频网采用正交频分复用(OFDM)技术对抗多径信道带来的符号间干扰(ISI)[4]。虽然OFDM技术能有效抑制ISI，但却无法解决部分子信道因深衰落而导致的信号检测概率低的问题。目前，在集中式多天线OFDM系统中，采用空频码技术解决该问题[5-9]。

已有的空频码技术不能直接应用于单频网中，这是因为，现有的空频码技术针对的都是不同发射天线信号同步到达接收端的集中式多天线系统。而在单频网中，分布在不同地理位置的各个发射天线到达接收端的距离可能不同，各发射天线的信号就可能异步到达接收端。因此，为了提高单频网的系统性能，有必要研究适合于单频网的发射信号设计方法。

1 系统模型

考虑一个带有MT根分布式发射天线的单频网。在发射端，数据经过调制、发射信号设计、N点OFDM调制、添加循环前缀后，从MT根发射天线发射出去。

假设发射端与带有MR根集中式天线的接收端之间的信道是准静态信道，将发射天线p(TXp)与接收天线q(RXq)之间的信道建模为带有抽头系数的抽头延迟线模型：

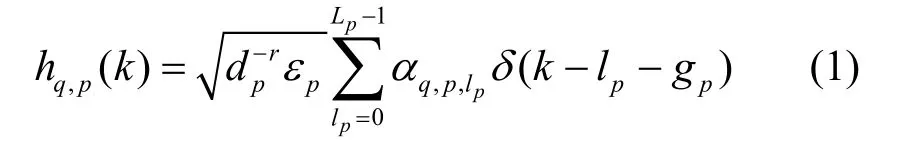
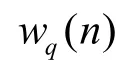
2 发射信号设计

2.1 信号设计准则

基于上述系统模型，本节通过误对概率分析，得到发射信号设计应该遵循的准则。

基于式(2)，接收端MR根天线收到的所有子载波上的信号可以表示为：

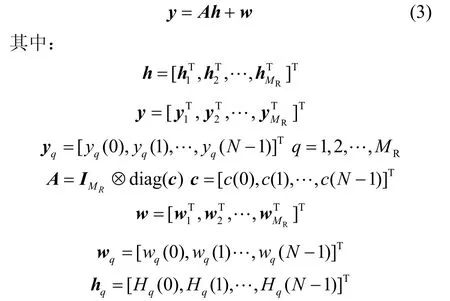
为了降低误对概率，根据式(4)，发射信号的设计应该遵循以下准则：

(1) 使R尽可能大的分集度准则；

(2) 使分集乘积尽可能大的分集乘积准则。

2.2 分集度分析和达到理论分集度的信号设计

基于式(4)，首先分析系统能获得的分集度，然后设计能达到该分集度的发射信号。

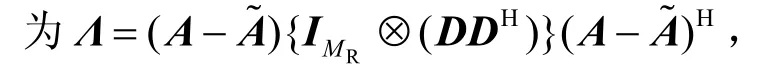
如前所述，系统能获得MRZ分集度的前提是diag(c−c)满秩。为了达到该目的，可以根据格理论[12]，将发射信号设计为c=Gb，其中G为满足N×N的生成矩阵[12]，b为调制后、等待信号设计的信息。如此设计得到的发射信号就能达到MRZ的分集度。

2.3 满分集发射信号设计

根据节2.2的分析，系统在理论上能达到的最大分集度为MRL，以下设计2种能获得最大分集度的发射信号。

2.3.1 获满分集发射信号方法一

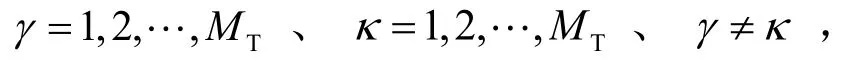
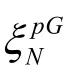
2.3.2 获满分集发射信号方法二

2.4 优化发射信号

在假设能达到最大分集度的前提下(在实际情况中，此场景是存在的)，基于上述发射信号的分集乘积可以表示为：

图1 v=1时的相位因子图

图2 选择恰当v时的相位因子图

3 仿真验证

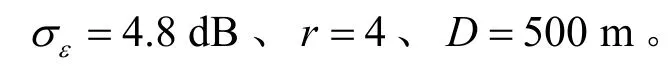
图3 仿真场景示意图。

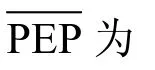
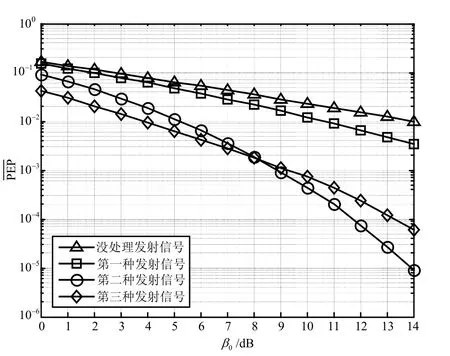
图4 不同发射信号设计方案的仿真结果

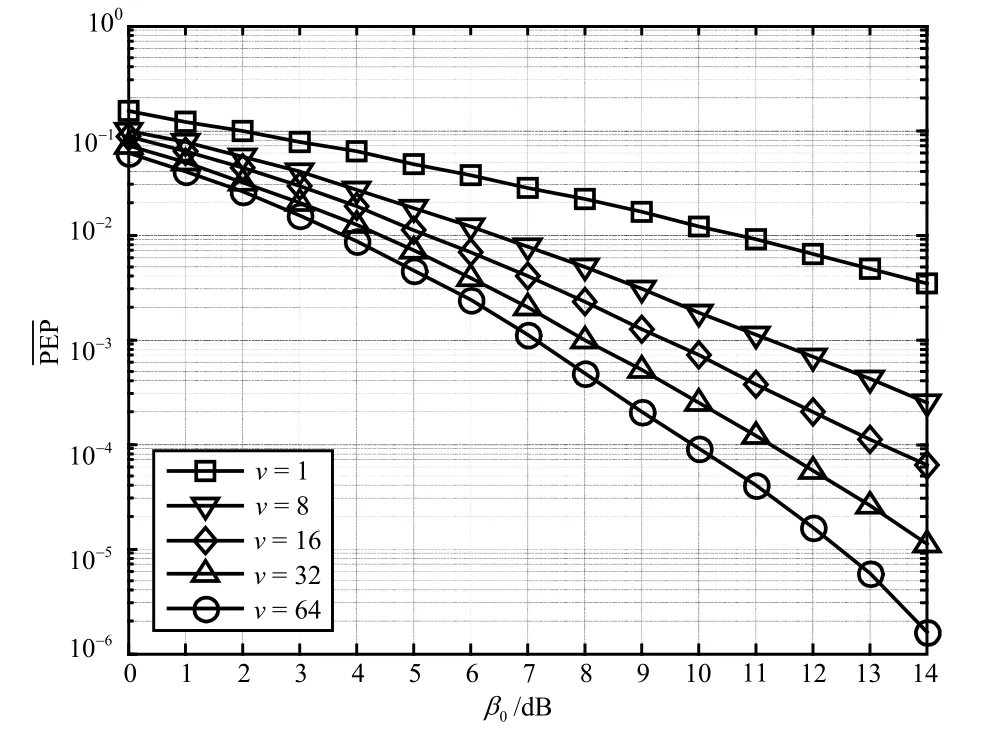
图5 发射信号优化设计方案

4 结 论

本文针对单频网，设计了具有满分集度的发射信号，提出了基于异步时延的子载波交织分组信号优化方法，该方法在接收机位置与性能之间建立了一种折中关系。仿真结果表明，优化后的发射信号能获得5～9 dB的增益。

[1] MATTSSON A. Single frequency networks in DTV[J].IEEE Transactions on Broadcasting, 2005, 51(4): 413-422.

[2] PARK S I, LEE J Y, KIM H M, et al. Transmitter identification signal analyzer for single frequency network[J]. IEEE Transactions on Broadcasting, 2008, 54(3):383-393.

[3] SUNG I P, HOMIN E, YONG T L, et al. Equalization on-channel repeater for terrestrial digital multimedia broadcasting system[J]. IEEE Transactions on Broadcasting,2008, 54(4): 752-760.

[4] CIMINI L J. Analysis and simulation of a digital mobile channel using orthogonal frequency division multiplexing[J].IEEE Transactions on Communications, 1985, 33(7):665-675.

[5] FAZEL F, JAFARKHANI H. Quasi-orthogonal spacefrequency and space-time-frequency block codes for MIMO OFDM channels[J]. Transactions on Wireless Communications, 2008, 7(1): 184-192.

[6] SU W, SAFAR Z, RAY K J. Towards maximum achievable diversity in space, time, and frequency: performance analysis and code design[J]. IEEE Transactions on Wireless Communications, 2005, 4(4): 1847-1857.

[7] SU W, SAFAR Z, RAY K J. Full-rate full-diversity space-frequency codes with optimum coding advantage[J].IEEE Transactions on Information Theory, 2005, 51(1):229-249.

[8] TORABI M, AISSA S, SOLEYMANI M R. On the BER performance of space-frequency block coded OFDM systems in fading MIMO channels[J]. IEEE Transactions on Wireless Communications, 2007, 6(4): 1366-1373.

[9] WANG Jun, LIU Shou-yin. A new high rate differential space-time-frequency modulation for MIMO-OFDM[J].Journal of Electronic Science and Technology of China,2007, 5(3): 193-198.

[10] SIWAMOGSATHAM S, FITZ M P, GRIMM J. A new view of performance analysis of transmit diversity schemes in correlated rayleigh fading[J]. IEEE Transactions on Information Theory, 2002, 48(4): 950 -956.

[11] HORN R A, JOHNSON C R. Matrix analysis[M].Cambridge, UK: Cambridge University Press, 1986.

[12] WANG G, XIA X G. On optimal multilayer cyclotomic space-time[J]. IEEE Transaction on Information Theory,2005, 51(3): 1102-1135.