复杂网络链路预测
2010-04-26吕琳媛
吕琳媛
(弗里堡大学物理系 瑞士 弗里堡 CH-1700)
网络中的链路预测(link prediction),既包含了对未知链接(existent yet unknown links)的预测,也包含了对未来链接(future links)的预测。链路预测作为数据挖掘领域的研究方向之一在计算机领域已有较深入的研究,研究的思路和方法主要基于马尔科夫链和机器学习。文献[2]应用马尔科夫链进行网络的链路预测和路径分析。之后,文献[3]将基于马尔科夫链的预测方法扩展到自适应性网站(adaptive web sites)的预测中。此外,文献[4]提出一个回归模型在文献引用网络中预测科学文献的引用关系,方法不仅用到了引文网络的信息,还有作者信息、期刊信息以及文章内容等外部信息。应用节点属性的预测方法还有很多,如文献[5]利用网络的拓扑结构信息以及节点的属性,建立了一个局部的条件概率模型进行预测。文献[6]基于节点的属性定义了节点间的相似性,可以直接用于进行链路预测。虽然应用节点属性等外部信息的确可以得到很好的预测效果,但是很多情况下,信息的获得是非常困难的,甚至是不可能的,如很多在线系统的用户信息都是保密的。另外,即使获得了节点的属性信息,也很难保证信息的可靠性,即属性是否反映了节点的真实情况,如在线社交网络中,很多用户的注册信息都是虚假的。更进一步,在能够得到节点属性的精确信息的情况下,如何鉴别出哪些信息对网络的链路预测是有用的,哪些信息是没用的,仍然是个问题。
最近几年,基于网络结构的链路预测方法受到越来越多的关注。相比节点的属性信息而言,网络的结构更容易获得,也更加可靠。同时,该类方法对于结构相似的网络具有普适性,从而避免了对不同网络需要机器学习获得一些特定的参数组合。文献[7]提出了基于网络拓扑结构的相似性定义方法,并分析了若干指标对社会合作网络中链路预测的效果。另外一类链路预测方法是基于网络结构的最大似然估计。2008年,文献[8]提出了一种利用网络的层次结构进行链路预测的方法,并在具有明显层次结构的网络中表现很好。此外,利用随机分块模型[9]预测网络缺失边和错误边的链路预测方法。值得一提的是,该篇文章第一次提到网络错误连边(spurious links)的概念,即在网络已知的链接中很可能存在一些错误的链接,比如人们对蛋白质相互作用关系的错误认知。
链路预测问题受到来自不同领域、拥有不同背景的科学家的广泛关注,首先是因其重大的实际应用价值。如在生物领域研究中,蛋白质相互作用网络和新陈代谢网络,节点之间是否存在链接,或者说是否存在相互作用关系,是需要通过大量实验结果进行推断的。已知的实验结果仅仅揭示了巨大网络的冰山一角。仅以蛋白质相互作用网络为例,酵母菌蛋白质之间80%的相互作用不为人们所知[11],而对于人类自身,人们知道的仅有可怜的0.3%[12-13]。由于揭示该类网络中隐而未现的链接需要耗费高额的实验成本,如果能够事先在已知网络结构的基础上设计出足够精确的链路预测算法,再利用预测的结果指导试验,就有可能提高实验的成功率,从而降低实验成本,并加快揭开该类网络真实面目的步伐。实际上,社会网络分析中也会遇到数据不全的问题,链路预测同样可以作为准确分析社会网络结构的有力的辅助工具[14-15]。除了帮助分析数据缺失的网络,链路预测算法还可以用于分析演化网络。如近几年在线社交网络发展非常迅速[16],链路预测可以基于当前的网络结构预测哪些现在尚未结交的用户“应该是朋友”,并将此结果作为“朋友推荐”发送给用户。如果预测足够准确,显然有助于提高相关网站在用户心目中的地位,从而提高用户对该网站的忠诚度。另外,链路预测的思想和方法,还可以用于在已知部分节点类型的网络(partially labeled networks)中预测未标签节点的类型,如用于判断一篇学术论文的类型[17]或者判断一个手机用户是否产生了切换运营商(如从移动到联通)的念头[18]。另外文献[10]所提出的对网络中的错误链接的预测,对于网络重组和结构功能优化也有重要的应用价值,如在很多构建生物网络的实验中存在暧昧不清甚至自相矛盾的数据[19],就有可能应用链路预测的方法对其进行纠正。
链路预测研究不仅具有广泛的实际应用价值,也具有重要的理论研究意义,特别是对一些相关领域理论方面的推动和贡献。近年来,随着网络科学的快速发展,其理论上的成果为链路预测搭建了一个研究的平台,使得链路预测的研究与网络的结构与演化紧密联系起来。因此,对于预测的结果更能够从理论的角度进行解释。与此同时,链路预测的研究也可以从理论上帮助人们认识复杂网络演化的机制。针对同一个或者同一类网络,很多模型都提供了可能的网络演化机制[20-21]。由于刻画网络结构特征的统计量非常多,很难比较不同的机制孰优孰劣。链路预测机制有望为演化网络提供一个简单统一且较为公平的比较平台,从而大大推动复杂网络演化模型的理论研究。另外,如何刻画网络中节点的相似性也是一个重大的理论问题[22],该问题和网络聚类等应用息息相关[23]。类似,相似性的度量指标数不胜数,只有能够快速准确地评估某种相似性定义是否能够很好地刻画一个给定网络节点间的关系,才能进一步研究网络特征对相似性指标选择的影响,因此,链路预测可以起到核心技术的作用。链路预测问题本身也带来了有趣且有重要价值的理论问题,就是通过构造网络系综(network ensemble),并借此利用最大似然估计方法进行链路预测的可能性和可行性研究,对链路预测本身以及复杂网络研究的理论基础的建立和完善起到推动和借鉴作用。
1 问题描述与评价方法

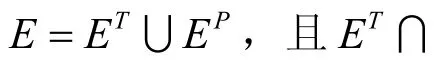
AUC可以理解为在测试集中的边的分数值有比随机选择的一个不存在的边的分数值高的概率,也就是说,每次随机从测试集中选取一条边与随机选择的不存在的边进行比较,如果测试集中的边的分数值大于不存在的边的分数值,就加1分;如果两个分数值相等,就加0.5分。独立地比较n次,如果有n′次测试集中的边的分数值大于不存在的边的分数,有n′次两分数值相等,则AUC定义为:显然,如果所有分数都是随机产生的,AUC=0.5。因此AUC大于0.5的程度衡量了算法在多大程度上比随机选择的方法精确。


Precision定义为在前L个预测边中被预测准确的比例。如果有m个预测准确,即排在前L的边中有m个在测试集中,则Precision定义为:显然,Precision越大预测越准确。如果两个算法AUC相同,而算法1的Precision大于算法2,说明算法1更好,因为其倾向于把真正连边的节点对排在前面。

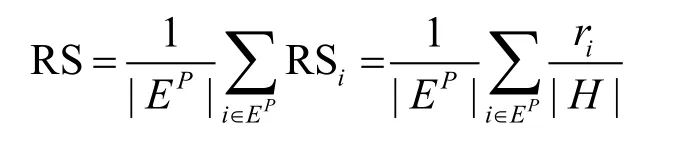
2 基于相似性的链路预测
应用节点间的相似性进行链路预测的一个重要前提假设就是两个节点之间相似性(或者相近性)越大,它们之间存在链接的可能性就越大。应注意,相似性并非一般意义上的相似性,而是指一种接近程度(proximity)。刻画节点的相似性有多种方法,最简单直接的方法就是利用节点的属性,如果两个人具有相同的年龄、性别、职业、兴趣等等,就说他们俩很相似。利用节点属性的相似性进行链路预测的前提,就是网络中的边本身代表着相似。另外一类相似性的定义完全基于网络的结构信息,称为结构相似性。基于结构相似性的链路预测精度的高低取决于该种结构相似性的定义是否能够很好地抓住目标网络的结构特征。如基于共同邻居的相似性指标,即两个节点如果有更多的共同邻居就更可能连边,在集聚系数较高的网络中表现非常好,有时甚至超过一些更复杂的算法。然而对于集聚系数较低的网络如路由器网络或电力网络等,预测精度就差很多。
2.1 基于局部信息的相似性指标
基于局部信息的最简单的相似性指标是共同邻居(common neighbors),也就是说两个节点如果有更多的共同邻居,则它们更倾向于连边。在共同邻居的基础上考虑两端节点度的影响,从不同的角度以不同的方式又可产生6种相似性指标,分别是Salton指标[27](也叫做余弦相似性)、Jaccard指标[28]、Sorenson指标[29]、大度节点有利指标(hub promoted index)[30]、大度节点不利指标(hub depressed index)和LHN-Ⅰ指标[22](由Leicht,Holme和Newman提出而得名),称这一类指标为基于共同邻居的相似性。
另一个只考虑节点度的相似性为优先连接指标(preferential attachment)。应用优先连接的方法可以产生无标度的网络结构,在该网络中,一条即将加入的新边连接到节点x的概率正比于节点x的度k(x)[31],因此新边连接节点x和y的概率正比于两节点度的乘积。该算法的复杂度较其他算法低,因为需要的信息量最少。
如果考虑两节点共同邻居的度信息,有Adamic-Adar(AA)指标[32],其思想是度小的共同邻居节点的贡献大于度大的共同邻居节点。因此根据共同邻居节点的度为每个节点赋予一个权重值,该权重等于该节点的度的对数分之一,即1/lgk。
文献[33]从网络资源分配(resource allocation)的角度提出一种新的指标,简称RA。考虑网络中没有直接相连的两个节点x和y,从x可以传递一些资源到y,而在此过程中,它们的共同邻居就成为传递的媒介。假设每个媒介都有一个单位的资源并且将平均分配传给它的邻居,则y可以接收到的资源数就定义为节点x和y的相似度。RA和AA指标最大的区别在于赋予共同邻居节点权重的方式不同,前者以1/k的形式递减,后者以1/lgk的形式递减。可见,当网络的平均度较小时RA和AA差别不大,但是当平均度较大时,就有很大的区别了。


表1 10种基于节点局部信息的相似性指标
文献[33]将上述10种基于节点局部信息的相似性指标在6个实际网络中进行实验,并比较其预测精确度[33]。6个网络分别为:蛋白质相互作用网络(PPI)、科学家合作网络(NS)、美国电力网络(Grid)、政治博客网络(PB)、路由器网络(INT)以及美国航空网络(USAir),它们的统计性质如表2所示。其中N、M分别表示网络的节点数和边数,Nc为网络的最大联通集团,如2 375/92表示PPI网络中有92个联通集团,最大联通集包含2 375个节点,e为网络的效率,C为网络集聚系数,r为同配系数,H为网络度异质性。预测结果如表3所示。所有结果均以AUC为预测精度评价指标。可见在10种算法中,RA表现最好,其次是CN,再次是AA。总的来说,PA表现最差,特别是在电力网络和路由器网络中,预测精度还不到0.5,意味着PA算法在这两个网络中预测精度还不如完全随机预测的好。

表2 6个实验网络的拓扑性质
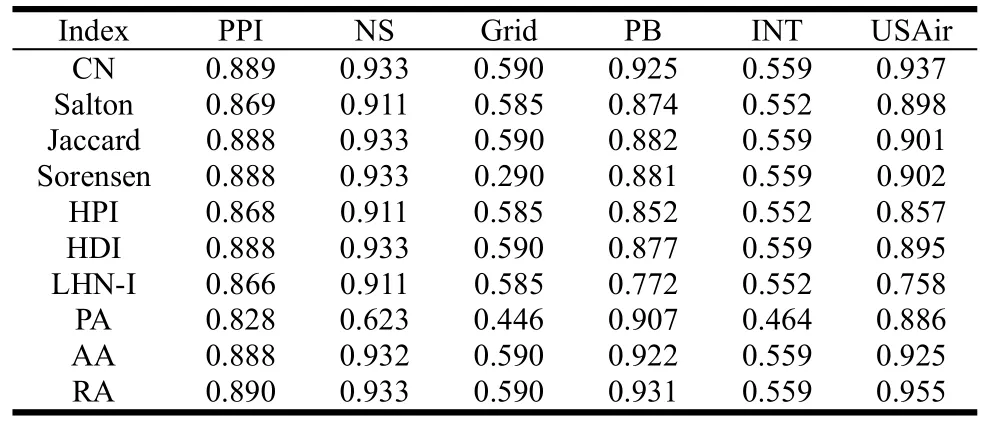
表3 10种基于节点局部信息的相似性在6个网络链路预测中的精度比较
2.2 基于路径的相似性指标
基于路径的相似性指标有3个,分别是局部路径指标(LP)[34]、Katz指标[35]和LHN-II[22]指标(与LHN-I在同一篇文章中提出)。

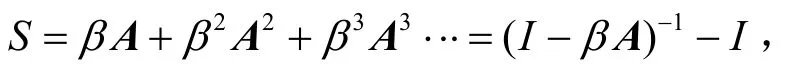
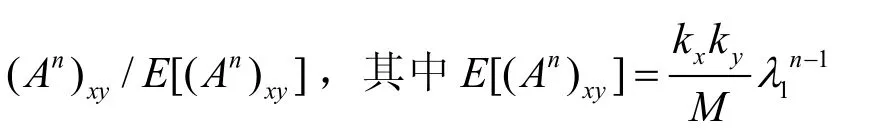
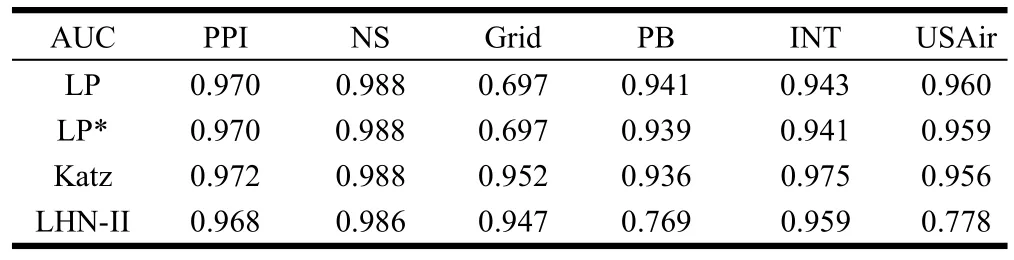
表4 基于路径的相似性指标在使用AUC衡量时的预测精度比较

表5 基于路径的相似性指标在使用Precision衡量时的预测精度比较
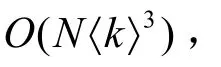
2.3 基于随机游走的相似性指标
有一类相似性算法是基于随机游走定义的,包括平均通勤时间(average commute time)[37]、Cos+指标[38]、有重启的随机游走(random walk with restart)[39]、SimRank指标[40],以及新提出的两种基于局部随机游走的指标[36]。
(1) 平均通勤时间(average commute time)简称ACT。设m(x,y)为一个随机粒子从节点x到节点y需要走的平均步数,则节点x和y的平均通勤时间定义为:

其数值解可通过求该网络拉普拉斯矩阵的伪逆+L获得[37],即:



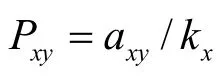



关于RWR的一种快速算法参见文献[41],该指标已被应用于推荐系统的算法研究中[42]。
(4) SimRank指标简称SimR。它的基本假设是,如果两节点所连接的节点相似,则该两节点相似[40]。它的自洽定义式为:



(6) 叠加的局部随机游走指标(superposed random walk)简称SRW[36]。在LRW的基础上将t步及其以前的结果加总便得到SRW的值,即:

这个指标的目的就是给邻近目标节点的点更多的机会与目标节点相连。
文献[36]比较了上述两种基于局部随机游走和基于全局随机游走的ACT和RWR指标在5个不同领域的网络中的链路预测效果。该5个网络分别为美国航空网络(USAir)、科学家合作网(NS)、电力网络(Grid)、蛋白质相互作用网络(PPI)和线虫神经网络(C.elegans),其拓扑结构的统计特性展现于表6。注意,与节3.1中数据不同的是,这里只考虑了最大联通集。〈k〉和〈d〉分别表示平均度和平均最短距离。

表6 5个网络最大连通集的统计特征

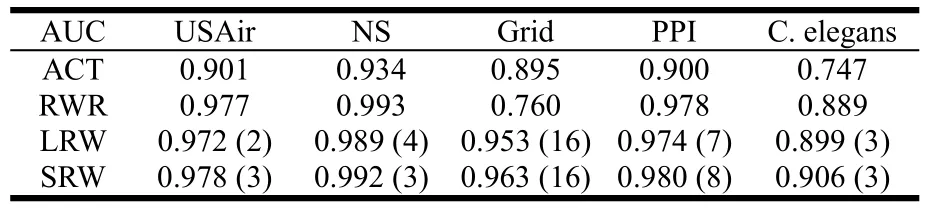
表7 4种基于随机游走的算法在使用AUC衡量时的预测精度比较

表8 4种基于随机游走的算法在使用Precision衡量时的预测精度比较
2.4 权重在链路预测中的作用
含权网络的链路预测是一个较重要的方向,但到目前为止还没有系统的研究工作,对于如何更好地运用权重的信息以提高链路预测的精确度还没有明确的答案。文献[43]将3种局部算法CN、AA和RA拓展为含权形式,定义如下:
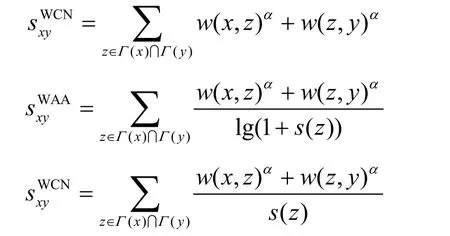


图1 美国航空网络预测精度与参数α的关系
此外,在科学家合作网中也发现了弱连接效应。但是在C.elegans线虫神经网络中结果恰恰相反,其最优参数值均大于1,意味着只有更加强调强连接,弱化弱连接,可称为链路预测的强连接效应,才能得到更好的预测结果。文献[43]随后运用motif分析方法定性解释了造成差异的原因,但是还不能进行定量的描述。含权网络的预测方法研究还具有很大的拓展空间,同样的网络结构,不同的含权方式在实际预测中起到的作用也可能不一样。要搞清这些问题,还需要更加深入细致的研究工作。
3 基于最大似然估计的链路预测
链路预测的另一类方法是基于最大似然估计的。文献[8]认为,很多网络的连接可以看作某种内在的层次结构的反映,基于此,文献[8]提出了一种最大似然估计算法进行链路预测,该方法在处理具有明显层次组织的网络(如恐怖袭击网络和草原食物链)时具有较好的精确度。但是,由于每次预测要生成很多个样本网络,因此其计算复杂度非常高,只能处理规模不太大的网络。文献[10]假设观察到的网络是一个随机分块模型(stochastic block model)[9]的一次实现,在该模型中节点被分为若干集合,两个节点间连接的概率只与相应的集合有关。文献[10]所提出的基于随机分块模型的链路预测方法,可以得到更好的结果。同时,该方法不仅可以预测缺失边,还可以预测网络的错误链接,如纠正蛋白质相互作用网络中的错误链接。基于最大似然估计方法的一个最大问题是计算复杂度太高,因此并不适合在规模较大的网络中应用。
3.1 层次结构模型[8]
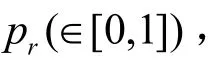
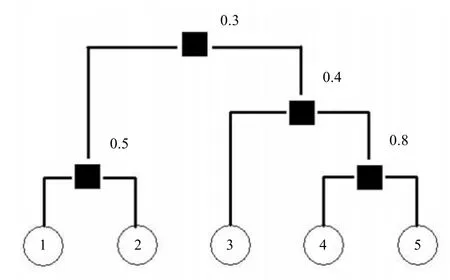
图2 用树形图表示网络的层次结构示例
给定一个网络G及和它相对应的一个树形图D,则这个树形图对目标网络G的似然估计值为:


(2) 随机选择一个内部节点r并考虑以其兄弟节点为根节点的子树集合B和以其儿女节点为根节点的子树集合C。
(3) 通过交换子树集合B和C中的子树获得新的树状图D′,注意D和D′不同。

(5) 当该马尔科夫链收敛于平稳时,开始生成可用的树形图,如5 000个。


3.2 随机分块模型[10]




式中Ω为所有可能的分块模型集合(实际运算中并不需要真正考虑所有的)。为方便计算,可将p(M)设定为一个常数。可信度越高表示越可能连边。随机分块模型不仅可以预测缺失边,还可以根据可信度判断哪些边是错误连边,如对蛋白质相互作用关系的错误认识。随机分块模型平均而言表现比层次结构模型好,尤其是在预测错误连边时。但是它与层次模型同样都存在计算时间复杂度高的问题。
4 概率模型
运用概率模型进行链路预测的基本思路就是建立一个含有一组可调参数的模型,然后使用优化策略寻找最优的参数值,使得所得到的模型能够更好地再现真实网络的结构和关系特征,网络中两个未连边的节点对连边的概率就等于在该组最优参数下它们之间产生连边的条件概率。如果将边的存在性(存在或不存在)看成是边的一种属性,那么链路预测问题就转变为预测边的属性问题[47]。两个常用的框架为概率关系模型框架(probabilistic relational models)[48]和有向无环概率实体关系框架(directed acyclic probabilistic entity relationship)[49]。它们的区别在于对数据库的表达方式不同,前者基于关系模型(relational models),后者基于实体关系模型(entityrelationship model)。
概率模型的优势在于较高的预测精确度,它不仅使用了网络的结构信息还涉及节点的属性信息。但是计算的复杂度以及非普适性的参数使其应用范围受到限制。
4.1 概率关系模型(PRMs)
概率关系模型是将概率模型和关系模型相结合的一种预测模型。概率关系模型包括3个网络:(1) 数据网络(data graph)即所谓的训练集,包含原始的数据信息;(2) 模型网络(model graph),分析数据网络得到的用于刻画网络主体属性之间的关系,该种关系既包括一类主体内部属性之间的关系,也包括不同主体属性之间的关系;(3) 推理网络(inference graph),是将模型网络与目标网络(测试集)相结合的网络,用于对目标网络的预测。根据模型网络的不同构造方法又可将概率关系模型分为贝叶斯网络关系模型(relational bayesian networks)[50]、马尔科夫网络关系模型(relational markov networks)[51]和关系依赖网络模型(relational dependency networks)[52-53]。




4.2 有向无环概率实体关系模型(DAPER)[49]
DAPER是以实体关系模型为基础所建立的模型,它将实体之间的关系也看成和实体一样重要。DAPER模型包括6类组成成分。
(1) 实体类(entity classes),即网络的实体,如大学数据库中的学生类和课程类。
(2) 关系类(relationship classes),即描述实体间的关系,如学生选择课程中的选择关系。
(3) 属性类(attribute classes),即实体或者关系的属性,如学生的智商,课程的难易程度等。
(4) 弧线类(arc classes),用于描述各个属性之间的关系,如学生的课程分数受到学生智商和课程难度的影响。属性关系构成的网络为有向无环网络(与RBN类似)。
(5) 局部概率分布类(local distribution classes),对某一属性类的条件概率分布,与PRMs中的条件概率类似。
(6) 限制条件类(constraint classes),衡量属性关系之间的限制条件。
文献[49]比较了该模型与PRMs模型的区别和联系。图3展现了在学生选择课程的例子中分别用DAPER和PRMs建立的模型,分别如图3a和3b所示。

图3 以大学数据中学生和课程为例的DAPER模型和PRMs模型
5 总结与展望
综上所述,无论是基于结构的相似性预测方法还是基于最大似然估计的方法,或是概率模型本质上都是通过对已知数据的尽可能真切的刻画的方法实现预测,但是它们的角度各自不同。基于结构相似性的方法只涉及网络的结构信息,主要从某一个角度对于网络的某一方面的结构特点进行刻画,如果目标网络的结构在该方面特征显著,即可得到较好的预测效果。虽然基于网络结构相似性的方法比较简单,计算复杂度相对较低,特别是基于局部结构的算法,但是各个方法在不同网络中的预测能力大不相同。目前还没有对算法性能和网络结构特征之间关系较深入的研究。对于比较复杂的网络,如含权网络、有向网络、多部分网络以及含有异质边的网络,如何通过结构信息进行预测的讨论甚少且不系统[43,55-56]。基于最大似然估计的方法虽然也是基于网络结构的,但是其针对的是整个网络结构而不仅仅局限于某一方面。该类方法由于计算复杂度较高,不可能应用于规模较大的网络。实验显示该类方法的预测精度也不是很高。概率模型是数据挖掘的传统模型,它可以同时考虑网络的结构信息和节点的属性信息,以求得到更好的预测效果。但是计算的复杂性以及节点外在属性信息在获取上的难度,造成该类方法应用的局限性。
最近十年,复杂网络研究在很多科学分支,包括物理、生物、计算机等掀起高潮[57],其中相当一部分研究立足于揭示网络演化的内在驱动因素。仅以无标度网络(scale-free networks)为例[58],已经报道的可以产生幂律度分布的机制就包括了富者愈富(rich-get-richer)机制[31]、好者变富(good-get-richer)机制[59]、优化设计(optimal design)驱动[60]、哈密顿动力学(hamiltonian dynamics)驱动[61]、聚生(merging and regeneration)机制[62]、稳定性限制(stability constraints)驱动[63],等等。可是,由于刻画网络结构特征的统计指标非常多,很难比较和判定什么样的机制能够更好再现真实网络的生长特性。利用链路预测有望建立简单的比较平台,能够在知道目标网络演化情况的基础上,量化比较各种不同机制对于真实生长行为的预测能力,从而可以大大推动复杂网络演化机制的相关研究。
与此同时,受益于复杂网络研究的快速发展,基于网络结构的链路预测方法有望在网络理论的帮助下得到发展和完善。一方面是如何以网络系综理论为基础,建立网络链路预测的理论框架,并产生对实际预测有指导作用的理论结论,如通过对网络结构的统计分析估算各个方法的可预测的极限,从而指导选择最佳的预测方法等;另一方面是如何通过网络的结构信息,借助复杂网络的分析工具,设计高效的算法处理大规模网络的链路预测问题。
尽管已有一些论文讨论了如何将链路预测的方法和思想与一些应用问题(如部分标号网络的节点类型预测[19,64-65]与信息推荐问题[33,55-66])相联系的可能性与方法,但是,目前尚缺乏对于大规模真实数据在应用层面的深入分析和研究。这方面的研究不仅仅具有实用价值,而且有助于揭示链路预测问题本身存在的优势与局限性。
[1] GETOOR L, DIEHL C P. Link mining: a survey[J]. ACM SIGKDD Explorations Newsletter, 2005, 7(2): 3-12.
[2] SARUKKAI R R. Link prediction and path analysis using markov chains[J]. Computer Networks, 2000, 33(1-6):377-386.
[3] ZHU J, HONG J, HUGHES J G. Using markov chains for link prediction in adaptive web sites[J]. Lect Notes Comput Sci, 2002, 2311:60-73.
[4] POPESCUL A, UNGAR L. Statistical relational learning for link prediction[C]//Proceedings of the Workshop on Learning Statistical Models from Relational Data. New York:ACM Press, 2003: 81-87.
[5] O’MADADHAIN J, HUTCHINS J, SMYTH P. Prediction and ranking algorithms for event-based network data[C]//Proceedings of the ACM SIGKDD 2005. New York: ACM Press, 2005: 23-30.
[6] LIN D. An information-theoretic definition of similarity[C]//Proceedings of the 15th Intl Conf Mach. Learn.. San Francisco, Morgan Kaufman Publishers, 1998: 296-304.
[7] LIBEN-NOWELL D, KLEINBERG J. The link-prediction problem for social networks[J]. J Am Soc Inform Sci Technol, 2007, 58(7): 1019-1031.
[8] CLAUSET A, MOORE C, NEWMAN M E J. Hierarchical structure and the prediction of missing links in networks[J].Nature, 2008, 453: 98-101.
[9] HOLLAND P W, LASKEY K B, LEINHARD S. Stochastic blockmodels: First steps[J]. Social Networks, 1983, 5:109-137.
[10] GUIMERA R, SALES-PARDO M. Missing and spurious interactions and the reconstruction of complex networks[J].Proc Natl Sci Acad USA, 2009, 106(52): 22073-22078.
[11] YU H, BRAUN P, YILDIRIM M A, et al. High-quality binary protein interaction map of the yeast interactome network[J]. Science, 2008, 322(5898): 104-110.
[12] STUMPF M P H, THORNE T, SILVA E de, et al.Estimating the size of the human interactome[J]. Proc Natl Sci Acad USA, 2008, 105(19): 6959-6964.
[13] AMARAL L A N. A truer measure of our ignorance[J].Proc Natl Sci Acad USA, 2008, 105(19): 6795-6796.
[14] SCHAFER L, GRAHAM J W. Missing data: Our view of the state of the art[J]. Psychol Methods, 2002, 7(2):147-177.
[15] KOSSINETS G. Effects of missing data in social networks[J]. Social Networks, 2006, 28(3): 247-268.
[16] KUMAR R, NOVAK J, TOMKINS A. Structure and evolution of online social networks[C]// Proceedings of the ACM SIGKDD 2006. New York: ACM Press, 2006:611-617.
[17] GALLAGHER B, TONG H, ELIASSI-RAD T, et al. Using ghost edges for classification in sparsely labeled networks[C]// Proceedings of the ACM SIGKDD 2008.New York: ACM Press, 2008: 256-264.
[18] DASGUPTA K, SINGH R, VISWANATHAN B, et al.Social ties and their relevance to churn in mobile telecom networks[C]// Proceedings of the EDBT’08. New York:ACM Press, 2008: 668-677.
[19] MERING C V, KRAUSE R, SNEL B, et al. Comparative assessment of large-scale data sets of protein-protein interactions[J]. Nature, 2002, 417: 399-403.
[20] ALBERT R, BARABASI A-L. Statistical mechanics of complex networks[J]. Rev Mod Phys, 2002, 74(1): 47-97.
[21] DOROGOVTSEV S N, MENDES J F F. Evolution of networks[J]. Adv Phys, 2002, 51(4): 1079-1187.
[22] LEICHT E A, HOLME P, NEWMAN M E J. Vertex similarity in networks[J]. Phys Rev E, 2006, 73: 026120.
[23] PAN Y, LI D H, LIU J G, et al. Detecting community structure in complex networks via node similarity[J].Physica A, 2010, 389(14): 2849-2857.
[24] HANELY J A, MCNEIL B J. The meaning and use of the area under a receiver operating characteristic (ROC)curve[J]. Radiology, 1982, 143: 29-36.
[25] HERLOCKER J L, KONSTANN J A, TERVEEN K, et al.Evaluating collaborative filtering recommender systems[J].ACM Trans Inf Syst, 2004, 22(1): 5-53.
[26] ZHOU T, REN J, MEDO M, et al. Bipartite network projection and personal recommendation[J]. Phys Rev E,2007, 76: 046115.
[27] SALTON G, MCGILL M J. Introduction to modern information retrieval[M]. Auckland: MuGraw-Hill, 1983.
[28] JACCARD P. Etude comparative de la distribution florale dans une portion des Alpes et des Jura[J]. Bulletin de la Société Vaudoise des Science Naturelles, 1901, 37:547-579.
[29] SORENSEN T. A method of establishing groups of equal amplitude in plant sociology based on similarity of species content and its application to analyses of the vegetation on Danish commons[J]. Biol Skr, 1948, 5(4): 1-34.
[30] RAVASZ E, SOMERA A L, MONGRU D A, et al.Hierarchical organization of modularity in metabolic networks[J]. Science, 2002, 297(5586): 1553-1555.
[31] BARABASI A-L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512.
[32] ADAMIC L A, ADAR E. Friends and neighbors on the web[J]. Social Networks, 2003, 25(3): 211-230.
[33] ZHOU T, LÜ L, ZHANG Y C. Predicting missing links via local information[J]. Eur Phys J B, 2009, 71(4): 623-630.
[34] LÜ L, JIN C H, ZHOU T. Similarity index based on local paths for link prediction of complex networks[J]. Phys Rev E, 2009, 80: 046122.
[35] KATZ L. A new status index derived from sociometric analysis[J]. Psychometrika, 1953, 18(1): 39-43.
[36] LIU W, LÜ L. Link prediction based on local random walk[J]. Europhys Lett, 2010, 89(5): 58007.
[37] Klein D J, Randic M, Resistance distance[J]. J Math Chem,1993, 12(1): 81-95.
[38] FOUSS F, PIROTTE A, RENDERS J M, et al.Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation[J]. IEEE Trans Knowl Data Eng, 2007,19(3): 355-369.
[39] BRIN S, PAGE L. The anatomy of a large-scale hypertextual Web search engine[J]. Comput Netw & ISDN Syst, 1998, 30(1-7): 107-117.
[40] JEH G, WIDOM J. SimRank: A measure of structuralcontext similarity[C]// Proceedings of the ACM SIGKDD 2002. New York: ACM Press, 2002: 538-543.
[41] TONG H, FALOUTSOS C, PAN J Y. Fast random walk with restart and its applications[C]// Proceedings of the 6th Intl Conf Data Min, Washington, D C, USA: IEEE Press,2006: 613-622.
[42] SHANG M S, LÜ L, ZENG W, et al. Relevance is more significant than correlation: Information filtering on sparse data[J]. Europhys Lett, 2009, 88(6): 68008.
[43] LÜ L, ZHOU T. Link prediction in weighted networks: The Role of Weak Ties[J]. Europhys Lett, 2010, 89(1): 18001.
[44] GRANOVETTER M S. The strength of weak ties[J]. Am J Sociology, 1973, 78(6): 1360-1380.
[45] RAVASZ E, BARABáasi A L. Hierarchical organization in complex networks[J]. Phys Rev E, 2003, 67: 026112.
[46] ZHOU C, ZEMANOVá L, ZAMORA G, et al. Hierarchical organization unveiled by functional connectivity in complex brain networks[J]. Phys Rev Lett, 2006, 97:238103.
[47] TASKAR B, WONG M F, ABBEEL P, et al. Link prediction in relational data[C]// Proceedings of the Neural Information Processing Systems(NIPS’03). Cambridge MA: MIT Press, 2004: 659-666.
[48] FRIEDMAN N, GETOOR L, KOLLER D, et al. Learning probabilistic relational models[C]// Proceedings of the 16th Intl Joint Conf Artif Intell(IJCAI). Stockholm, Sweden:[s.n.], 1999: 1300-1307.
[49] HECKERMAN D, MEEK C, KOLLER D. Probabilistic entity-relationship models, PRMs, and plate models[C]//Proceedings of the 21st Intl Conf Mach Learn, Banff,Canada: [s.n.], 2004: 55-60.
[50] HECKERMAN D, GEIGER D, CHICKERING D.Learning bayesian networks: the combination of knowledge and statistical data[J]. Mach, Learn, 1995, 20(3):197-243.
[51] TASKAR B, ABBEEL P, KOLLER D. Discriminative probabilistic models for relational data[C]// Proceedings of the UAI2002. Edmonton, Canada: [s.n.], 2002: 485-492.
[52] HECKERMAN D, CHICKERING D M, MEEK C, et al.Dependency networks for inference, collaborative filtering,and data visualization[J]. J Mach Learn Res, 2000, 1:49-75.
[53] NEVILLE J, JENSEN D. Relational dependency networks[J]. J Mach Learn Res, 2007, 8: 653-692.
[54] BESAG J. Statistical analysis of non-lattice data[J]. The Statistician, 1975, 24(3): 179-195.
[55] LESKOVEC J, HUTTENLOCHER D, KleinBerg J.Predicting positive and negative links in online social networks[C]// Proceedings of the WWW 2010. New York:ACM, 2010: 641-650.
[56] MURATA T, MORIYASU S. Link prediction of social networks based on weighted proximity measures[C]//Proceedings of the IEEE/WIC/ACM Intl Conf Web Intelligence. Washington, D C, USA: IEEE Press, 2007:85-88.
[57] BARABASI A-L. Scale-Free Networks: a decade and beyond[J]. Science, 2009, 325(5939): 412-413.
[58] CALDARELLI G. Scale-Free Networks: complex webs in nature and technology[M]. New York: Oxford Press, 2007.
[59] GARLASCHELLI D, CAPOCCI A, CALDARELLI G.Self-organized network evolution coupled to extremal dynamics[J]. Nature Physics, 2007, 3: 813-817.
[60] VALVERDE S, CANCHO R F, SOLE R V. Scale-free networks from optimal design[J]. Europhys Lett, 2002,60(4): 512-517.
[61] BAIESI M, MANNA S S. Scale-free networks from a Hamiltonian dynamics[J]. Phys Rev E, 2003, 68: 047103.
[62] KIM B J, TRUSINA A, MINNHAGEN P, et al. Self organized scale-free networks from merging and regeneration[J]. Eur Phys J B, 2005, 43(3): 369-372.
[63] PEROTTI J I, BILLONI O V, TAMARIT F A, et al.Emergent self-organized complex network topology out of stability constraints[J]. Phys Rev Lett, 2009, 103: 108701.
[64] ZHANG Q M, SHANG M S, LÜ L. Similarity-based classification in partially labeled networks[J]. Int J Mod Phys C, 2010, 21(6): 813-824.
[65] SEN P, NAMATA G, BILGIC M, et al. Collective classification in network data[J]. AI Magazine, 2008, 29(3):93-106.
[66] ZHOU T. Statistical mechanics of information systems:information filtering on complex networks[D]. Switzerland:University of Fribourg, 2010.
