混沌动力学Logistic模型在工程加密中的应用*

安建伟 何永前

(92852部队 湛江 524002)

1 引言

密码技术的基本思想是隐藏信息,未授权者不能得到信息的真实含义。加密就是对信息进行一组可逆的数学变换。如果我们采用软件完成数据加密的全过程,加密算法很容易被跟踪或篡改,并且实现加密算法的速度也受到限制等缺点将不可避免,这是由于软件加密自身特点决定的。由于数据加密领域中某些要求的特殊性,这些缺点带来了许多的问题。作为实现数据加密的一种重要方式,利用硬件电路实现数据加密具有软件无法比拟的高速度,尤其是利用专用电路实现某些算法,由于硬件加密的封闭性使加密算法很安全;如果计算机除了加密任务还有其他任务时,多种任务可以并行处理,计算机资源的利用率可大大提高。由于硬件加密具有以上突出优点,文章中以混沌密码学技术中的Logistic加密模型及现代ASIC设计等技术相结合,介绍具体的实现方法。

2 Logistic模型的基本特性

Logistic模型:

该模型只有一个变量 x,属于一维方程,但具有极其复杂的动力学规律。根据模型的定义,我们可以通过Logistic模型的分岔图可以直观了解 u的取值对迭代过程的影响和迭代结果的分布情况。

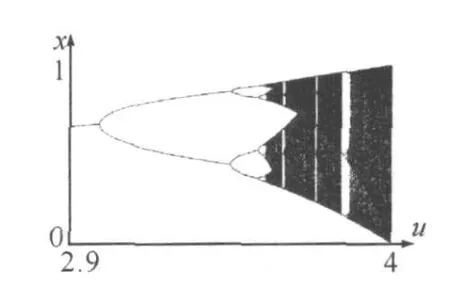
图1 Logistic映射的倍周期分岔图

在图1中以u为x轴,迭代多次的 xn的平均值为y轴,从图中可以看出该模型的迭代值强烈依赖 u,随着 u的不同 xn的最终分布可以分为两个区域:周期区和混沌区。当u的值很小时,当迭代次数趋于无穷大时,迭代值趋于一个定值;随着u的增大,迭代值的周期数以倍周期分岔的方式不断地增长。当u值大于3.57时,时间序列x0,x1,x2,…,xn,…依次排列得到的时间序列如同分布在区间[0,1]上的随机数,称之为混沌状态。

1)周期区

结论1 通过分析图1可以得出结论1:从周期2n-1到2n(n≥1),各分岔点un存在如下关系:

即各分岔点之间的距离以比例δ倍缩小,且δ为一无理数,这个数被称为费根包姆(Feigenbaum)δ常数。

结论2 通过分析图2我们得出每分岔一次,在x方向上的结构也在较小的标度上重复出现一次。周期2n中接近于xi处各x之间的距离 Δ 1,Δ 2,…,Δ n渐近的按因子α衰减:

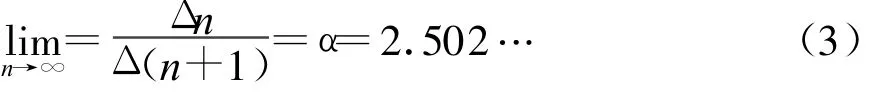
这里的费根包姆δ和α常数是一种普适常量,在倍周期分岔现象中具有普遍意义,与函数的形式无关。这两个常数也说明了倍周期分岔进入混沌是一种相当普遍的自然现象。

图2 周期2n中接近于xi处各 x之间的距离

2)混沌区

指出在混沌区也存在一些周期窗口,如周期3,5,6…等,并且通过这些周期又不断岔分出周期3*21,3*22,…等,最终进入混沌。混沌区中包含周期窗口,窗口区内又有混沌,这种不断重复的自相似结构有无穷多个层次,最终形成了我们现在看到的混沌区域。这里需要说明的是由于图形分辨率的限制,周期大于5的窗口在图1中没能被直观体现。

3 Logistic算法器的设计

在这一节中将着重介绍算法的设计思想和具体实现。

3.1 算法器数字电路的工作状态

在本次设计中要实现的迭代乘法算法为:

通过分析算法特点和加密过程,我们将实现一次加密工作乘法器内部要经历的状态分为四种状态,其状态图如图3所示。

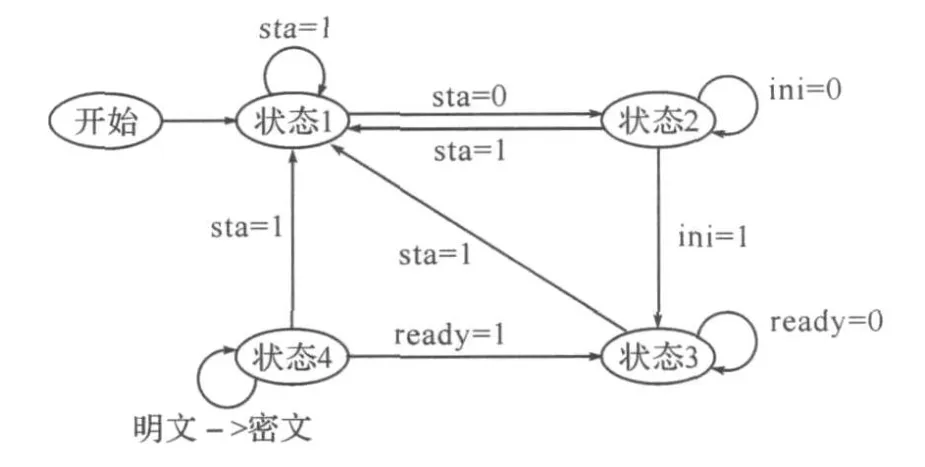
图3 Logistic映射乘法器的状态图

状态1:算法器处于复位状态,由输入信号sta控制

状态2:算法器处于初始化状态,X(64Bit),U(64Bit),NUM(迭代次数)的顺序依次输入初始化数据。

状态3:算法器完成规定的迭代次数后Ready有效,进入混沌态

状态4:算法器将需加密的数据在写信号有效时的第一个时钟周期生成密文,当密文被读走的同时,并准备好下一次加密数据时所需的数据,直至加密全过程结束,sta脚重新回到有效态。这样就可以周而复始的加密任意大小的文件。

3.2 Logistic模型算法的实现

为了保证迭代运算保持在混沌态,U的取值为3.8～4之间的数,在带入运算前先将U值通过除4转换为小数(64Bit),然后在每一次的迭代运算中积分两次乘以二。X◦(1-X)的积最大为1/4,所以在每一次的迭代运算不会产生大于1的数。

图4 乘法器的流程图

在实现迭代运算的设计中,设计的重点之一是超长度数据间的乘法。乘法运算占用的资源是最大的,如果对一些无效位不进行处理,64位与64位数据相乘后生成128位的结果中冗余数据还将占用大量的硬件资源;并且如果直接利用两个宽为64位的数据相乘,这里采用的Xilinx公司软件2.1版的Foundation将不能对设计进行综合(synthesis)形成宏单元。对算法进行改进,将两个64位数据A[63:0]、B[63:0]分成两部分同时相乘,将结果处理后再相加,得到精度仍为64位的积。这样在输出时宏单元就可以少占用64位的输出,内部珍贵的资源就可以节省下来。其工作流程图如图4所示。

在每一次Logistic运算中要进行两次乘法运算,为了节省资源,两次乘法用同一个乘法器,这样是以降低运算速度为代价,损失大约一半时间。通过外部控制信号(sel)和时钟信号(clk)来控制乘法运算的顺序:在第一个时钟周期完成z=x◦(1-x),有效数据取前[126:63]位,实现乘 2;在第2个时钟周期完成y=u◦z,有效数据仍取前[126:63]位,实现乘2。所得结果反馈给Logistic函数发生器的控制部分作为下一次运算的x。

在乘法器中,我们将每组的u值存入一个模块中,这个控制模块负责控制64×64位的乘法模块的输入和时钟信号;并且1-x产生64位有效数据的运算过程也由它完成。

4 算法器的具体实现及分析

4.1 算法器的原理图和时序仿真

u13是算法器中的控制器,通过握手信号和外部交换信息,控制每次加密过程中初始化、明文输入、和密文输出的全过程;H1实现乘法的宏器件,u13利用控制信号线控制乘法器实现Logistic算法。

图5 算法器的原理图

我们将原理图通过综合过程后,利用产生的时间延迟参数进行后时序仿真来校验设计功能。因为篇幅原因,这里仅分析算法器在数据加密状态下的时序。

图6 加密过程中的读写时序

通过后时序仿真可以看出,算法器达到设计要求。当将初始化数据写入算法器,输入要求的时钟数目后,算法器进入混沌状态,ready变为高电平。通过写命令wr将要加密的明文数据流和混沌产生密钥流异或形成密文,然后通过读命令rd将密文取走。由于明文写入和密文输出公用一个总线,所以设计使用读信号控制数据总线方向引脚dir的电气特性。这里读信号和写信号的操作均是在其有效后的第一个时钟开始进行,写信号需一个时钟,读信号需两个时钟。从图6中可以看出硬件完成每项动作的时序,包括施加控制信号到得到响应的延时,如rd和dir边沿间的延时等,这些特征只能在后时序仿真中才能观察到。通过对仿真后时序结果进行分析后重新设计,有效避免这些特殊延时可能导致的设计对象的逻辑功能混乱。

4.2 乘法器的原理图和时序仿真

本设计依据顶层设计的方法实现了乘法器MMM,由它具体实现乘法,乘数和被乘数均为64位。其管脚定义如表1所示。

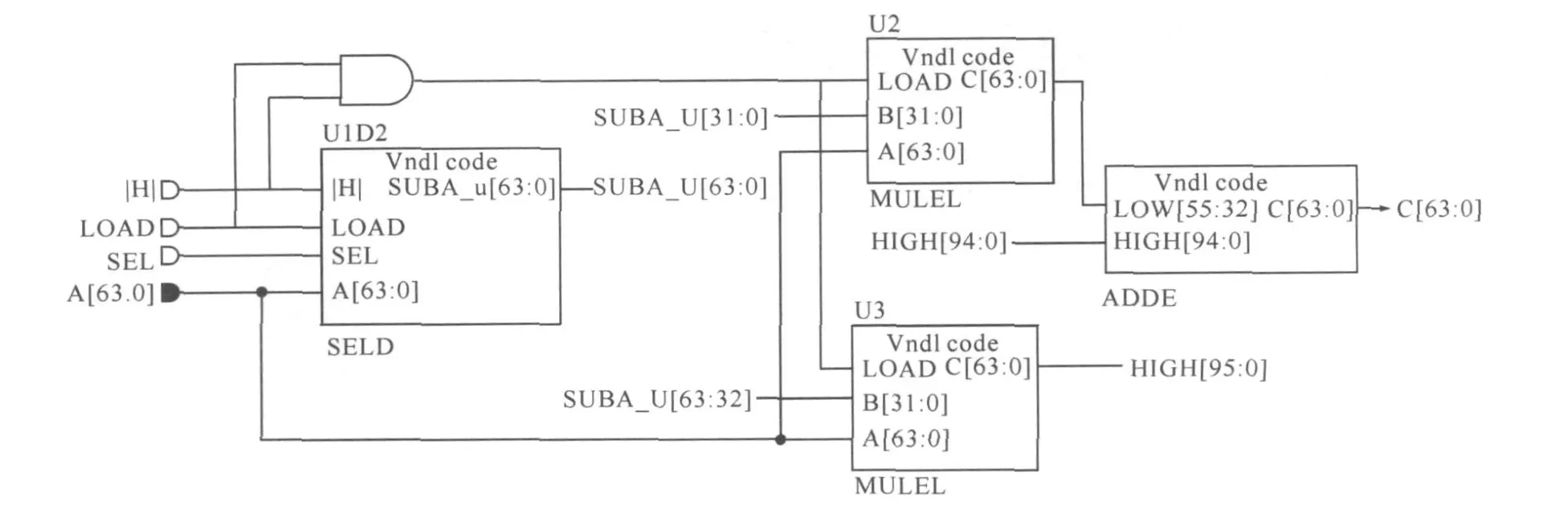
图7 乘法运算的具体实现的原理图

表1 乘法器的管脚定义

同样在后时序仿真时,我们也测试了作为算法器中最重要的部件—乘法器的功能。

通过后时序仿真图8可以清楚地看到乘法器实现两次乘法的全过程,这里需要说明的是:因为进行每次的乘法运算均在load的上升沿发生,load由控制器的clk_out信号驱动。而clk_out信号是由读信号和时钟信号共同驱动的,所以要求读密文时的读信号的有效时间长度必须大于两个时钟周期。

图8 乘法器的后时序仿真图

5 结语

通过分析Logistic算法的特点和加密过程的特点,本文利用Foundation软件设计了[64:64]的超长二进制乘法器和完成加密解密功能的算法器,并且通过后时序仿真利用模拟外部控制信号实现了算法器的初始化,进入规定的混沌状态,明文的输入、密文的输出和退出混沌状态等规定操作,并且在连续加密(解密)解密过程中,完成单字节加密(解密)过程所需时间仅需300ns左右,速度是软件不能比拟的,设计结果极为理想。

[1]黄润生.混沌及其应用[M].武汉:武汉大学出版社,2000:112～175

[2]孟宪元.可编程ASIC集成数子系统[M].北京:电子工业出版社,1998:175～186

[3]蔡国权,宋国文,于大鹏.Logistic映射混沌扩频序列的性能分析[J].通信学报,2000(1):60～63

[4]王亥,胡健栋.Logistic-Map混沌扩频序列[J].电子学报,1997(1):19～23

[5]XILINX公司.The Programmable Logic Data Book.XILINX公司,2000:5_1～5_19

[6]Lin.T,Chua.L.O.A New class of pseudo-random number generator based on chaos in digital filters.International Journal of Circuit Theory anApplications,1993,21:473～480

[7]曾繁泰,陈美金.VHDL程序设计[M].北京:清华大学出版社,2000:5～22

[8]Heidari-Bateni.G,Mcgillem.C.D.A chaotic direct sequence spread-spectrum communication system[J].IEEE Trans Communications,1994,42:1524～1527

[9]Chua.L.O,Yao.Y,Yang.Q.Generation randomness from chaos and constructing chaos with desired randomness.Int.J.Circuit Theory and Applications,1990,18:215～240