太平湾电站机组盘车方法的改进
2010-04-21宁淑贤
宁淑贤
(太平湾发电厂,辽宁 丹东 118000)
太平湾电站是鸭绿江干流上的第四级水电站,位于鸭绿江下游辽宁省丹东市境内,与朝鲜平安北道朔州方山里隔江相望,坝址下游距丹东40 km,距上游长甸电站29 km。电站由东北勘测设计院设计,水利水电第六工程局承建,主设备由哈尔滨电机厂有限责任公司制造。发电机型号为SF47.5-88/12640(1、2号机组)与SF47.5-104/12640 (3、4号机组),水轮机型号为ZZ560A-LH-800,励磁机型号为ZLS285/60-14。机组轴系由水轮机轴、发电机主轴、发电机转子中心体、发电机副轴、励磁机轴、操作油管等组成。
1 机组盘车的目的
盘车的目的是检查大轴是否铅垂;检查转动部件连接部分是否同心和存在曲折;检查镜板与主轴是否垂直;检查转子中心体与发电机主轴、发电机副轴是否垂直;检查机组轴线是否合格;为轴线处理和调整提供了可靠的第一手资料;根据盘车结果计算并分配各部导轴承瓦的间隙等。因此,机组盘车是一项非常重要的工作。
2 传统盘车方法存在的弊端
自太平湾电站机组1985年投入运行至今,一直沿用传统的8点等角盘车方式,即在盘车前,首先在推力头或上导轴领处将轴进行8等分,并按机组旋转相反方向依次编号,然后分别在受油器上操作油管、中操作油管、励磁机整流子、上集电环、下集电环、上导轴领、推力头、发电机主轴法兰、水导轴领等9个典型部位的x、y方向上各设1块百分表,用于测量以上部位的盘车摆度,再根据测量结果通过手工绘制净摆度曲线的方法求最大净全摆度及其方位。这些方法的缺点如下。
a.由于机组转动部件质量高、惯性大,在操作时随机性较大,要准确停留在某个特定的轴号上非常困难,不是转过头就是转不到位,使盘车数据与特定轴号对应不准,增加盘车摆度计算的误差。
b.用人工方法绘制净摆度曲线的步骤是:根据盘车测得各轴号下的数据,计算出各典型部位的净摆度大小;以轴号为横坐标、净摆度为纵坐标,按照相同的比例,将各净摆度点放入坐标系内;将各点轻轻连上;看摆度曲线是否符合正弦或余弦规律;检查曲线的波峰和波谷是否相差180°;删除个别偏离理论曲线的点;波峰和波谷的垂直距离即为最大净全摆度的大小;曲线上波峰对应的位置即为最大净全摆度的方位。但这种方法跟技术人员的业务水平和现场实际经验关系很大,求取结果往往会因人而异。
c.传统等角盘车方法在处理盘车数据时,无法有效克服测量断面表面质量对数据处理结果的影响。
以上缺点导致计算盘车摆度的大小及方位具有一定的盲目性,直接影响了下一步主要旋转部件找中心及轴线处理量的大小和方向确定,降低了盘车质量,直接影响了下一步轴线处理量的大小和方向,增加了轴线处理的重复次数,延误检修工期。
3 多点任意角盘车软件的开发
3.1 机组摆度特性及数学模型的建立
水电机组盘车时旋转轴的摆度特性在理论上遵循一条正弦曲线,曲线的横坐标是盘车角度,纵坐标是盘车摆度值。机组盘车的摆度数据处理,其实质就是将一系列实测的有一定离散性的数据点,拟合成一条理论的正弦或余弦曲线问题。由于传统盘车方法存在着不可克服的弱点,摆度计算又不能从整体考虑,由此产生误差是显而易见的。因此,依据最小二乘法原理,推导出机组盘车摆度计算公式,按计算公式进行实际盘车数据与理论盘车数据拟合,从而可方便地计算出各典型部位的摆度大小和方位,并将其编制成计算机程序,制成具有可视化的计算机界面,在机组盘车测量完毕后,只要将各测量部位的角度和绝对摆度录入到计算机中,即可计算出最大净全摆度及其方位,极大方便了检修作业,起到事半功倍的效果。
设正弦曲线的数学模型为
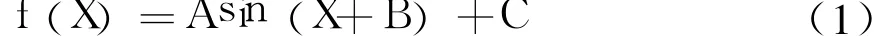
式中 X——盘车点对应的角度,(°);
f(X)——对应盘车角度下的理论摆度值, 0.01mm;
A——摆度曲线的幅值,0.01 mm;
B——摆度曲线的初相,(°);
C——摆度曲线在纵坐标上的偏移值,0.01 mm。
3.2 正弦曲线的拟合及摆度计算
在表达式(1)中,A、B、C均为待定常数量。确定常数A、B、C最理想的情形是能使曲线f (X)=A sin(X+B)+C经过盘车点的测值所标出的各点,但实际上根本不可能。由于盘车中摆度测量存在测量误差和随机误差,使得在这些盘车点上的测量值程度不同地偏离了这条摆度正弦曲线,因为无法知道测量过程中各点的实际误差,只能运用最小二乘法原理对全部误差作整体考虑,找出一条最接近实测摆度值的正弦曲线。因此要求选取这样的A、B、C,使曲线f(X)=Asin(X+B)+ C在X1,X2,……,Xn处的理论函数值f(X1),f (X2),……,f(Xn)与实际测的盘车摆度值Y1, Y2,……,Yn相差都很小,要达到这样的要求,可以考虑选取常数A、B、C,使得S=∑ni=1[f(Xi) -Yi]2最小来保证每个偏差的绝对值都很小。这种根据偏差的平方和为最小的条件来选择常数A、B、C的方法,称为最小二乘法。
将S看成自变量A、B、C的一个三元函数,那么该问题就可归结为求函数S=S(A、B、C)在哪些点处取得最小值的问题。由求多元函数的极值理论可知,上述问题可以通过求方程组(2)的解来解决。
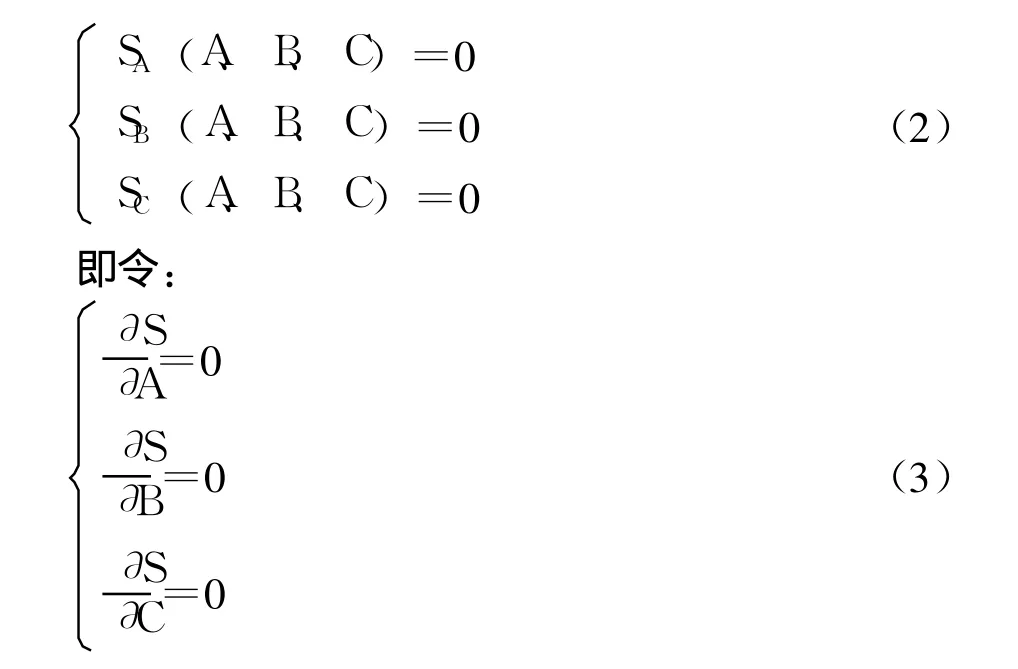
对以上方程组演绎求解发现,这是一组非线性方程组,求解非常困难,因此考虑作如下变换。
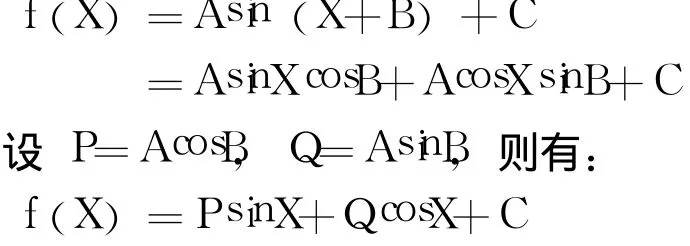
可推导出A=P2+Q2,最大摆度对应的方位角X即为摆度曲线上波峰对应的角度,由f(X) =PsinX-IQcosX+C的导数来确定。
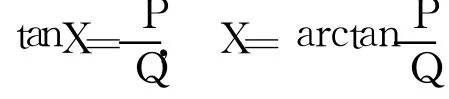
即令f′(X)=PcosX-QsinX=0可求得:当P>0、Q>0时X值的范围为0°<X<90°;当P>0、Q<0时X值的范围为90°<X<180°;
当P<0、Q<0时X值的范围为180°<X<270°;
当P<0、Q>0时X值的范围为270°<X<360°。
经过上面变量代换后,偏差平方和S变成P、Q、C的函数。同理使S=S(P、Q、C)取得最小值的P、Q、C也满足方程组

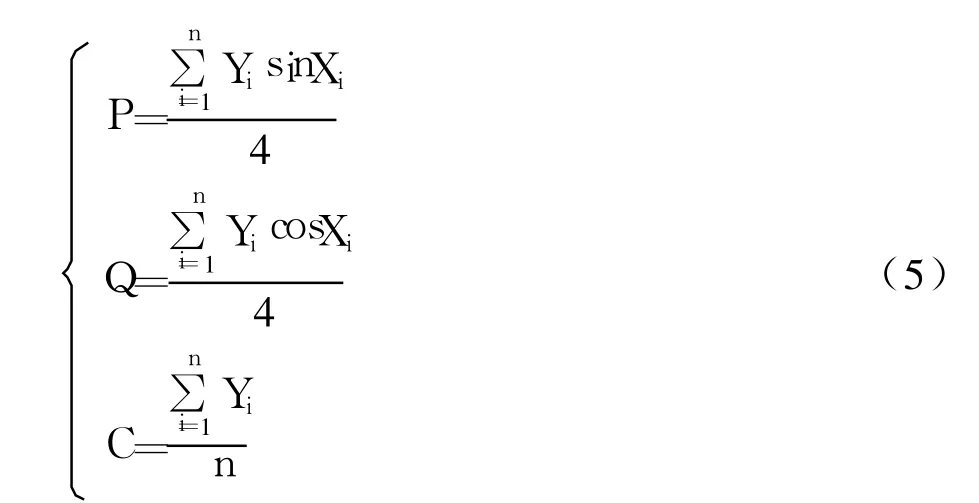
3.3 软件开发
前面建立了多点任意角盘车的数学模型,但由于其盘车摆度的计算公式相当繁琐,将其编制成计算机程序,盘车时将盘车数据作现场处理就十分方便。利用Visual Basic6.0软件将上述公式编成计算机程序,制成具有可视化的计算机界面,并与数据库连接,使计算和绘图就变得简单。
4 新方法在机组盘车过程中的应用
2008年9月,太平湾电站4号机组A级检修开始,对自行设计开发的多点任意角盘车软件进行首次应用,取得了较好的效果,盘车不再受转角限制,只需在数据测量完毕后,将其录入到图1所示的计算机界面中,即可计算出机组各测量部位最大净全摆度及其方位,见图2。又通过对理论值与实际值比较,检验在盘车过程中所测得的实际数值偏离理论数值的程度和误差,使数据分析更直观,见图3。根据用最小二乘法进行曲线拟合得到的数据,给下一步轴线处理指明了方向。
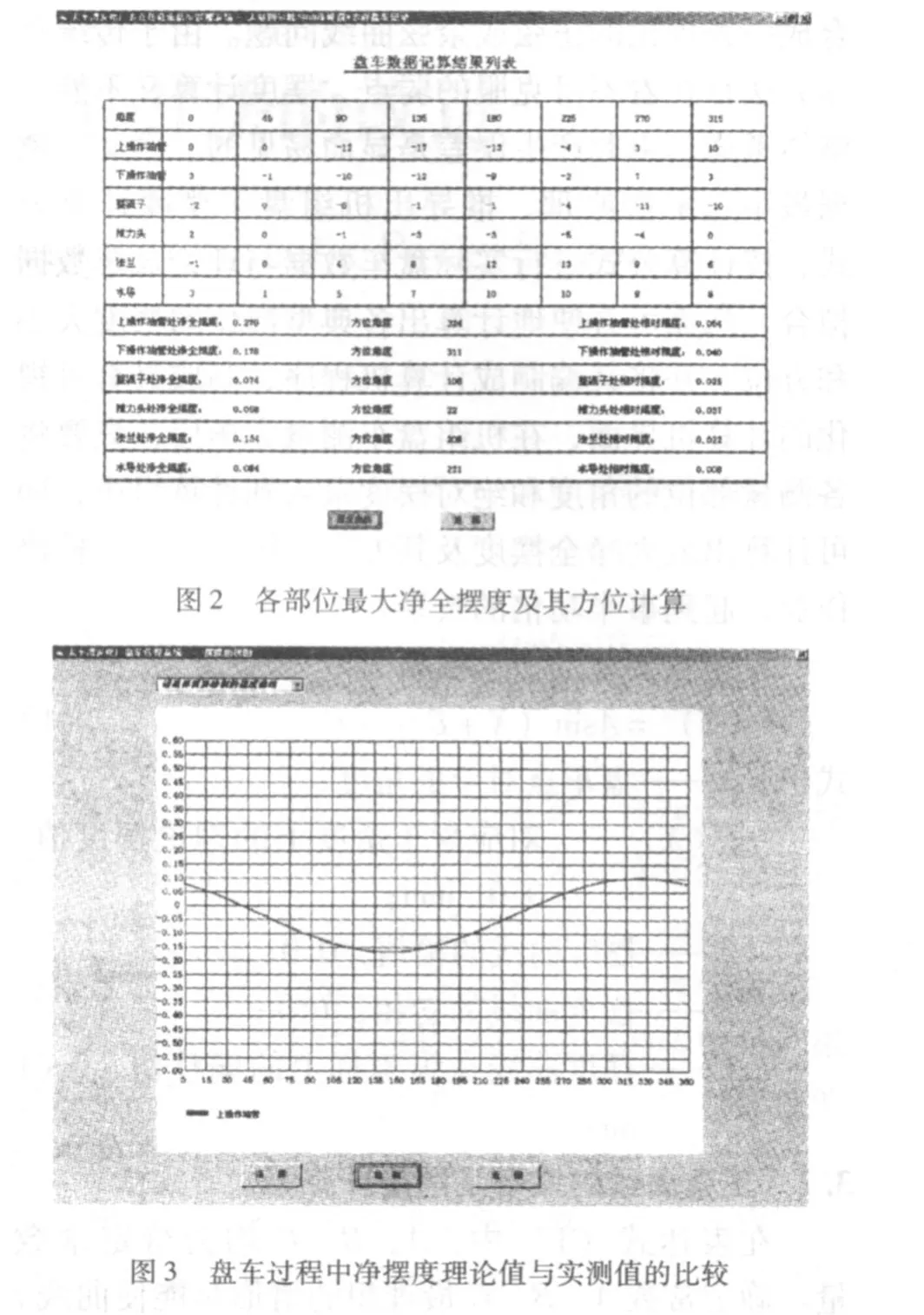

图1 盘车数据录入窗口
5 结论
机组盘车是机组安装及检修中的重要环节,对盘车数据进行分析处理的精度和准确度,对下一步机组主要旋转部件找中心、轴线处理及导轴承瓦间隙计算、分配的影响是直接的,为了能够更精确地处理盘车数据,应用最小二乘法的原理,编制开发多点任意角盘车软件,在检修现场对盘车数据进行处理,能够更好地消除误差,使数据处理结果真实可信。该方法理论严谨、工艺简单、操作方便;盘车摆度计算精确、速度快;减少了检修工期,提高了经济效益;具有较大的推广应用价值。
