机械设备振动源特性研究

严 斌，吴文伟，刘忠族

（中国船舶科学研究中心，江苏 无锡214082）

1 引 言

机械噪声作为舰艇主要噪声源之一，一直以来都是舰艇减振降噪所研究的重点。而准确地掌握设备激励特性是开展机械系统定量声学设计的基础。因此，对于机械设备振动源特性的研究具有重要的工程意义。

从上世纪70年代开始，国外专家对机械设备激励特性进行了大量深入研究，并取得许多具有工程实用性的成果。其中最关键的是选取何种参数来描述设备振动的固有特性以及获取这些参数的方法。Breeuwer和Tukker[1]提出了用“自由速度”描述源强度。Juha Plunt[2]在1982年的inter-noise会议上指出自由悬挂的条件可以由安装在软弹簧上来近似满足。Mondot和Petersson[3]于1987年引入源描述符来表征源特性。此后Petersson、Fulford、Gibbs[4-7]将结构声源描述符拓展到多点、多激励耦合情况下，着重研究了互耦合情况。Moorhouse[8-10]提出用特征功率来描述结构声源特性，着重研究源参数的测量，尤其是机脚和基础导纳的在线测量。国内梁军[11]进行了设备弹性到刚性安装下机脚响应的换算。武汉船舶设计研究所原春晖[12]着重研究了激励力的间接估算方法。相比国外，国内在源研究上还存在很大差距。

本文重点研究机械设备在自由悬置和弹性安装下自由速度的测量，以及改变安装基础阻抗后机脚响应的换算关系。

2 源特性描述

2.1 源参数选择

传统描述振动源特性的方法有机脚处激励力、机脚振动加速度（速度）、输入基座的功率流等。然而，由于被测结构振动与安装条件有关，所以这些数据只对所研究的特定装置有效，它们并不是设备固有的源特性的描述。近年来提出自由速度与钳制力的概念，且不随安装条件改变。而它们之间又可以通过结构阻抗和导纳相互转换。由于力不易测量验证，本文将选取自由速度和机脚导纳作为源描述参数。

2.2 源参数与响应输出关系

图1（a）给出了源和基础连接处的输入输出情况，其中vfs为自由速度、Fs和Fr分别为源与接受体连接点处作用力、vs和vr为源与接受体在连接点处速度、M0和Mr分别为源与接受体在连接点处导纳。众所周知，用自由速度vfs或者是钳制力F∞是表征设备“源强”比较科学的参数。自由速度和钳制力与机脚导纳M0和机脚阻抗Z0有如下关系：

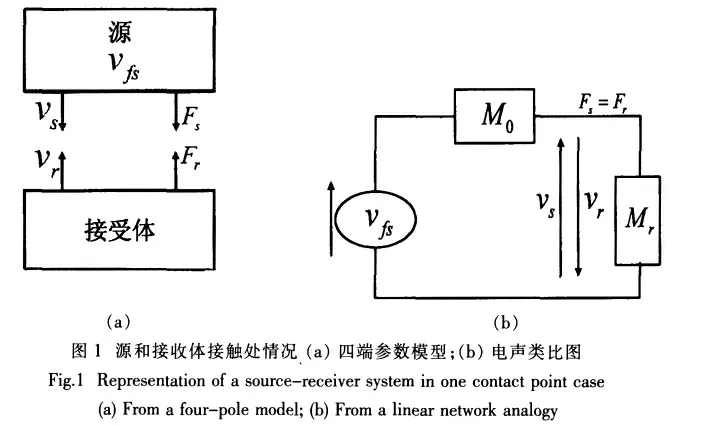
从本质上讲，自由速度是不约束源时的工作速度，钳制力是驱动源运动所必须的力。这两个量如果不采用折衷的办法都不可能轻易测得。导纳和阻抗都是源结构的固有属性。

根据图1（b）易得：

（3）式和（4）式中源输出速度vs和接收体速度vr相等，以后统一用连接速度vc表示。作用在接触面上的力Fs和Fr大小相等方向相反。 由（3）式和（4）式得：

由（5）式得出，在已知源参数的情况下，只需提供接收体的导纳就可以进行在安装状态下源和接受体的连接处响应的换算。然而在很多情况下自由速度不易获取，这就需要在不同安装状态下进行响应的换算。

2.3 不同安装状态下连接处响应换算关系

对（5）式移项变形

由于自由速度是不变量，那么设备在两种安装状态下有如下关系：

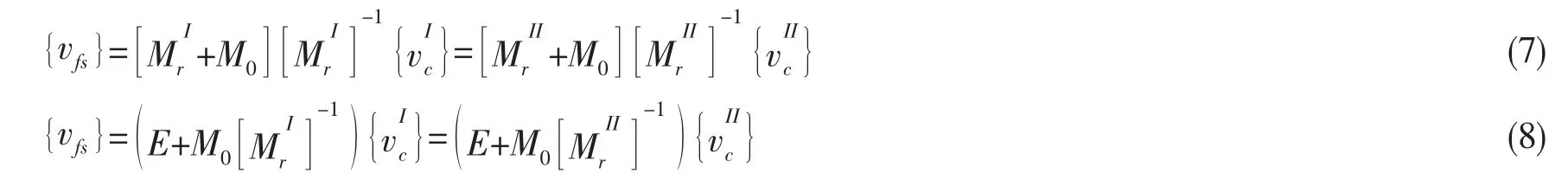
从（6）式得到自由速度与连接速度的关系：

当M0Zb<

3 源参数测量

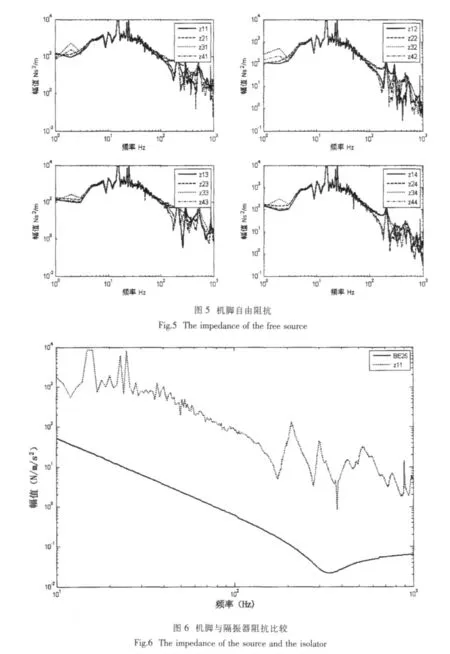
3.1 自由速度测量

自由速度的测量关键在于如何实现“自由”条件。弹性悬挂是比较理想的自由状态，但是对于大型设备这并不容易实现，所以安装在弹性支撑上才是工程上可取的。ISO9611-1996给出了有关自由速度的测量方法，但是其中就弹性安装测量时弹性元件的选择并没有给出一个明确的范围。

图2给出了一台设备在自由悬置条件下以及安装在BE10，BE15，BE25隔振器上测量机脚响应的试验照片。所有的测试都在阻抗平台上进行，且仅考虑垂直方向的响应。

图3给出了转速为1 800rpm时设备自由悬置（悬吊频率3Hz）以及安装在隔振器上（安装频率11Hz）四个机脚的振动加速度级。为了便于比较，这里使用三分之一倍频程来表示。测量结果显示悬吊与弹性安装的结果基本一致。因此，将设备安装在隔振器上测得的速度作为自由速度是可信的。但是在不同的隔振器之间以及隔振器与自由悬吊情况下在个别频率点上还是存在一点差别。对于同一台设备，不同型号的隔振器对响应的影响有多大，这与机脚的阻抗有关，根据设备状态在测试自由速度时应选取什么型号的隔振器将在下面介绍。

3.2 机脚导纳测量

前面已经讲到，弹性安装测量自由速度时要求Zb<

对比1号机脚（z11）与BE25隔振器的输入加速度阻抗（见图6），它们的幅值相差都在10倍以上，BE10，BE15的阻抗小于BE25，失配程度更大。而测得响应（见图3）差别很小。这就是说当机脚阻抗和隔振器阻抗的失配程度达到10倍以上时，测得的速度可作为自由速度。一般而言，只要不超过隔振器额定载荷，其选择应越软越好。

4 不同安装条件下机脚响应的换算值与实测值对比

前面测量了自由速度以及机脚导纳作为源参数，若提供安装基础的阻抗信息即可进行响应的换算。以下试验依然仅考虑垂直方向的响应。从自由速度测试中可知设备在基础阻抗比较小的情况下机脚响应的变化不会很明显。因此本文选择将设备安装在阻抗较大的基础上进行测量。基础阻抗形式也是由简单到复杂。这样由之前测量的源的参数加上安装基础的阻抗（导纳）利用（9）式就可以进行不同安装条件下响应的换算，并可以与实际测试结果对比。考虑实际运算过程中存在相位问题，处理方法是以1号机脚为参考点，其余机脚响应与之做互谱，取互谱的相位作为它们之间的相位差。计算公式如下：。G11，Gjj为在四个机脚测的自功率谱；∠（Gj1）为与参考点互谱的相位角。这样以矩阵的形式进行计算就能换算出4个机脚的响应。

在前边进行悬吊与安装在隔振器上机脚响应比较时发现在少数频率点上它们幅值上存在一点差异。为了考察它们谁更接近我们要求的自由速度，这里利用公式（9）将BE10隔振器上的响应换算成自由速度与自由悬吊下的响应进行比较如图7，图中sus表示悬吊测试值、prd表示换算值、BE10表示隔振器上测试值。

从四个机脚不同途径得到的自由速度对比情况来看，安装在隔振器上与从隔振器换算来的自由速度是一致，这说明公式（9）的正确性。在十几赫兹时有些偏差，这可能是安装频率造成的。而自由悬吊在40-100Hz依然略小。下面分别使用自由悬吊与安装在隔振器上机脚响应作为自由速度进行换算。

4.1 试验一

采用四个“ ”型过渡结构连接阻抗平台，首先进行基础阻抗的测量，由于与阻抗平台接触端响应近似为零，因此不存在通过阻抗平台的传递，Zb为一对角矩阵。有了接收结构的阻抗，结合前边的源参数即可进行响应的换算。另外利用（9）式可以从安装在隔振器上的响应换算出此时的响应。然后安装上设备，调整转速，记录下实际的机脚响应。图8和图9分别给出了使用悬吊方法以及安装在隔振器上测得自由速度换算转速1 800rpm时机脚1/3倍频程各频带振动加速度级（带级），图中实线为测试值，虚线为换算值。

4.2 试验二

试验二将一块厚钢板四角垫起，通过螺栓固定在阻抗平台上。这样的基础只满足导纳测量条件，然后再换算出阻抗。重复试验一的步骤换算机脚响应。安装上设备实际测量结果与之对比。这里只通过隔振器响应换算。图10为转速1 800rpm时机脚1/3倍频程振动加速度级换算值（虚线）与实测值（实线）。

从整体看来，两种换算情况，使用隔振器上的响应来换算效果更好。事实上设备通过螺栓安装在隔振器上，测得的自由速度数据涵盖了一些连接部分不易考察的耦合分量，特别在低频时，机脚响应测试信噪比不足，因此很难换算准确。对于两次试验，曲线无论趋势还是幅值都表明换算基本接近实测情况，能够满足工程应用要求。

5 结 论

通过上述试验值与计算值的对比分析，可以得到如下几点结论：

（1）采用自由速度和机脚导纳作为源参数来描述源特性是合理的。

（2）自由速度测量可选择在与机脚阻抗失配十倍以上的隔振器上测量，一般地，只要不超过隔振器额定载荷，其选型应越软越好。

（3）弹性安装下测量的响应既可以作为自由速度，又可以用其进行不同安装条件下响应的换算，此法比自由速度的换算更具实用性。

（4）本文中使用矩阵描述方法来表征多点激励条件下接触面上力与速度的关系，试验证明该换算方法是可行的。

[1]Breeuwer R,Tukker J C.Resilient mounting systems in building[J].Applied Acoustics,1976,9:77-101.

[2]Juha Plunt.The use of experimental structure-borne sound source data for prediction[C]//Inter-Noise 82.San Francisco,1982.

[3]Mondot J M,Petersson B.Characterization of structure-borne sound sources:The source descriptor and the coupling function[J].Journal of Sound and Vibration,1987,114(3):507-518.

[4]Petersson B A T,Gibbs B M.Use of source descriptor concept in studies of multi-point and multi-directional sources[J].Journal of Sound and Vibration,1993,168(1):157-176.

[5]Fulford R A,Gibbs B M.Structure-borne sound power and source characterization in multi-point-connected system part I:Case studies for assured force distributions[J].Journal of Sound and Vibration,1997,204(4):659-677.

[6]Fulford R A,Gibbs B M.Structure-borne sound power and source characterization in multi-point-conneted system part II:About mobility function and free velocities[J].Journal of Sound and Vibration,1997,220(2):203-224.

[7]Petersson B A T,Gibbs B M.Towards a structure-borne sound source characterization[J].Applied Acoustics,2000,61:325-343.

[8]Moorhouse A T.On the characteristic power of structure-borne sound sources[J].Journal of Sound and Vibration,2001,248(3),441-459.

[9]Elliott,Moorhouse,Pavic.Characterisation of structure-borne sound source using indenpent and in-situ measurement[C]//19th International Congress on Acoustics.Madrid,2007.

[10]Elliott,Moorhouse.Characterization of structure-borne sound sources from using measurement in-situ[C]//Euronoise.Paris,2008.

[11]梁 军.不同环境下机械设备振动激励特性的转换关系研究[J].中国舰船研究,2007,2(2):52-56.

[12]原春晖,朱显明.舰艇机械设备噪声振动特性的测试方法[J].舰船科学技术,2006,2:30-33.