基于LBM方法的圆盘等速入水空泡的数值模拟

张 珂，颜 开，褚学森，程贯一

（中国船舶科学研究中心，江苏 无锡214082）

1 引 言

自由面流动广泛存在于自然界和日常生活中，其特点表现为存在可移动的自由表面。有着广泛的工程应用背景。例如，在风浪环境中航行的船舶，其摇荡过程中艏艉会与水面发生砰击，严重时所产生的冲击力可导致船舶局部结构的破坏；船舶液舱中的自由面随着船身的摇摆发生晃荡，产生对舱壁的冲击载荷。恶劣海况中的甲板上浪也属于自由面流动。物体入水问题是典型的自由面流动问题。空投鱼雷在入水过程中，包含撞水(溅水)、流动形成、空泡打开、空泡面闭合、空泡深闭合直至空泡消失等一系列相继发生的现象，在该过程中强烈的入水载荷有可能引起结构强度破坏问题，也可能影响内部仪器的正常使用。入水空泡将影响入水初期弹道。对入水载荷、入水空泡和入水弹道的研究一直是国内外的重要研究课题。

研究物体入水的数值模拟方法可有多种，如质点标记（MAC）法[1]、VOF方法[2]、光滑粒子流体动力学（SPH）方法[3]、边界元法[4]等等。这些方法分别具有其自身的优势和存在的问题。当自由面变化非常剧烈时，尤其是当气液发生掺混时，自由面边界变得模糊不清，这些方法往往难以奏效，必须寻求更加有效的方法。格子Boltzmann方法是一种新兴的数值模拟方法，它基于统计物理学，具有独特的粒子特性。其微观动力学背景使得它具有许多其它基于N-S方程的数值方法所没有的独特优点[5]。格子Boltzmann方法的基本思路是：按照分子运动论的观点，流场是运动粒子的宏观效应；该方法将时间和空间完全离散，将流场划分为格子；流体被抽象成大量的微观粒子，并且这些微观粒子根据某种简单的运动规则在离散的格点上进行迁移和碰撞；粒子分布函数的演化在宏观上反映流体的运动规律，流场的密度、速度等宏观量可由粒子分布函数计算得到。

本文尝试采用一种格子Boltzmann单相自由面模型[6]进行物体入水空泡流动的数值模拟研究，获得入水空泡的变化规律。该模型的特点是忽略系统中气相对液相的动力学影响，适用于具有大密度比的气液两相流动。同时这一尝试将为在模拟更为复杂的自由面流动中采用格子Boltzmann方法打下基础。

2 计算模型

2.1 格子Boltzmann模型

标准的格子BGK模型[7]如下式所示：

其中，i表示格子速度方向，fi（x,t）表示在t时刻x位置在i方向具有速度ci的粒子的分布函数，τ为无量纲松弛时间，为平衡态分布函数。

平衡态分布函数选择如下：

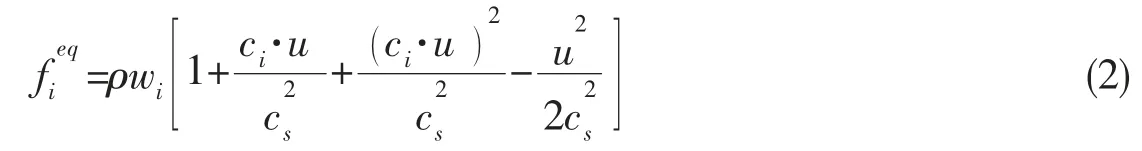
宏观量的速度、密度等可通过格点各方向的粒子分布函数的适当运算得到：

其中n为格点离散速度方向的个数。

本文采用D3Q19模型离散速度，其离散速度模型如图1所示，格子声速。 当i=0时，权重wi=1/3；当i=1～6时，权重wi=1/18；当i=7～8时，权重wi=1/36。

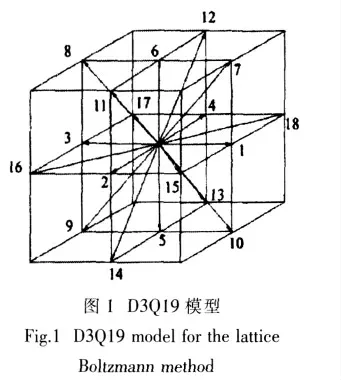
2.2 单相自由面模型

Thuery[6]提出的格子Boltzmann单相自由面模型适用于大密度比的气液两相流动，其特点是忽略了系统中气相对液相的动力学影响。该模型中流场被划分为三类格点：液相格点、界面格点、气相格点。其中液相格点被液相完全充满，气相格点完全被气相充满，界面格点既包含液相也包含气相。并且气相格点和液相格点之间必须有界面格点存在。

每个格点都定义了流体体积分数ε＝m/ρ，其中m为格点的质量，ρ为格点密度。根据定义有：气相格点ε=0，界面格点0<ε<1，液相格点ε＞1。界面格点质量的变化直接通过相邻格点的粒子分布函数计算得到。对于x位置的界面格点，其相邻格点位置为x+ciΔt，ci为离散速度。则该方向的质量流量可按下式计算：

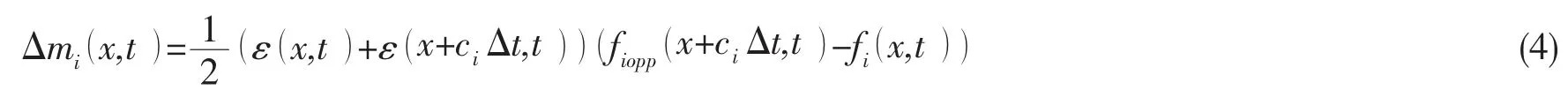
其中下标iopp表示i的反方向。下一时间步x位置界面格点的质量为

由于气相格点的物理量在计算中被忽略，从气相格点迁移至液相格点的分布函数需要根据宏观边界条件进行重构：

其中ρA为气体压力对应的密度，下标iopp代表i的反向，u为x位置界面流体的速度。对于边界处界面格点，本文采用文献[8]中提出的使用重构的分布函数的方式处理，以获得边界处更为合理的自由面速度。

在界面运动的过程中，界面格点可能变为气相格点或者液相格点。界面的重构则根据质量与密度的关系来决定。若碰撞步后界面格点的流体体积分数ε>1+κ（κ为选取的小量，如κ=10-3），则界面格点转变为液相格点，它周围的气相格点则相应地变为界面格点；若ε<-κ，则界面格点转变为气相格点，它周围的液相格点也需要相应地变为界面格点。为了保持质量守恒，格点类型的转换完成后需要对多余的质量根据界面的法向进行重新分配。

2.3 重力的处理和边界处理

由于重力对入水空泡的发展规律有重要的影响，本文引入重力的影响。重力的作用是一种额外的体积力，在格子Boltzmann方法中可以通过改变动量的方法引入重力的影响[9]。平衡态分布函数由新的速度=u+τg求得，即其中τ为松弛时间。

由于本文采用的LBM模型为弱可压缩模型，因此在物体入水过程中会产生一系列的压力波。这些压力波在计算边界处会发生反射，而产生的反射波会对流场的压力分布产生影响，甚至影响自由面的形状。为了减弱该影响，本文的入口边界采用了基于插值的叠加格式[10]。四周的流场边界则采用了充分发展边界处理格式。圆盘处采用半步长反弹格式。

3 计算结果与分析

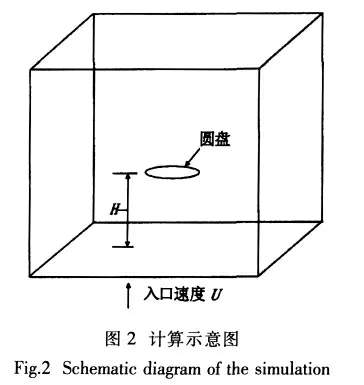
本文进行了不同Froude数下圆盘垂直等速入水的全三维数值模拟，并将计算结果与Bergmann等人[4]的实验结果进行了比较。实验中，入水圆盘的半径为30mm，在三种工况中，平板分别以0.5m/s、1m/s和2m/s速度入水，则相应的Froude（定义为Fr=U2/gR）数分别为0.85，3.4和13.6。数值模拟计算示意图如图2所示，计算域的网格数为150×150×180。采用流体运动而圆盘静止的方式进行圆盘垂直等速入水的模拟，计算中圆盘半径R=15，初始水深H=40，重力加速度g=0.000 005，边界入口速度U等于圆盘入水速度。

图3－5分别给出了对应Fr=0.85、3.4、13.6等三种工况的入水空泡的数值模拟结果。

图6为Bergmann等人给出的对应Fr=0.85、3.4、13.6等三种工况（分别对应图6（a）、（b）、（c））的实验照片[4]）。该实验与现有的其它圆盘入水实验的区别是其底部通过连杆严格控制了圆盘入水的速度。实验照片中白色的线条系文献[4]作者采用边界元方法得到的计算结果，时间τ表示该时刻到空泡闭合所需的时间。

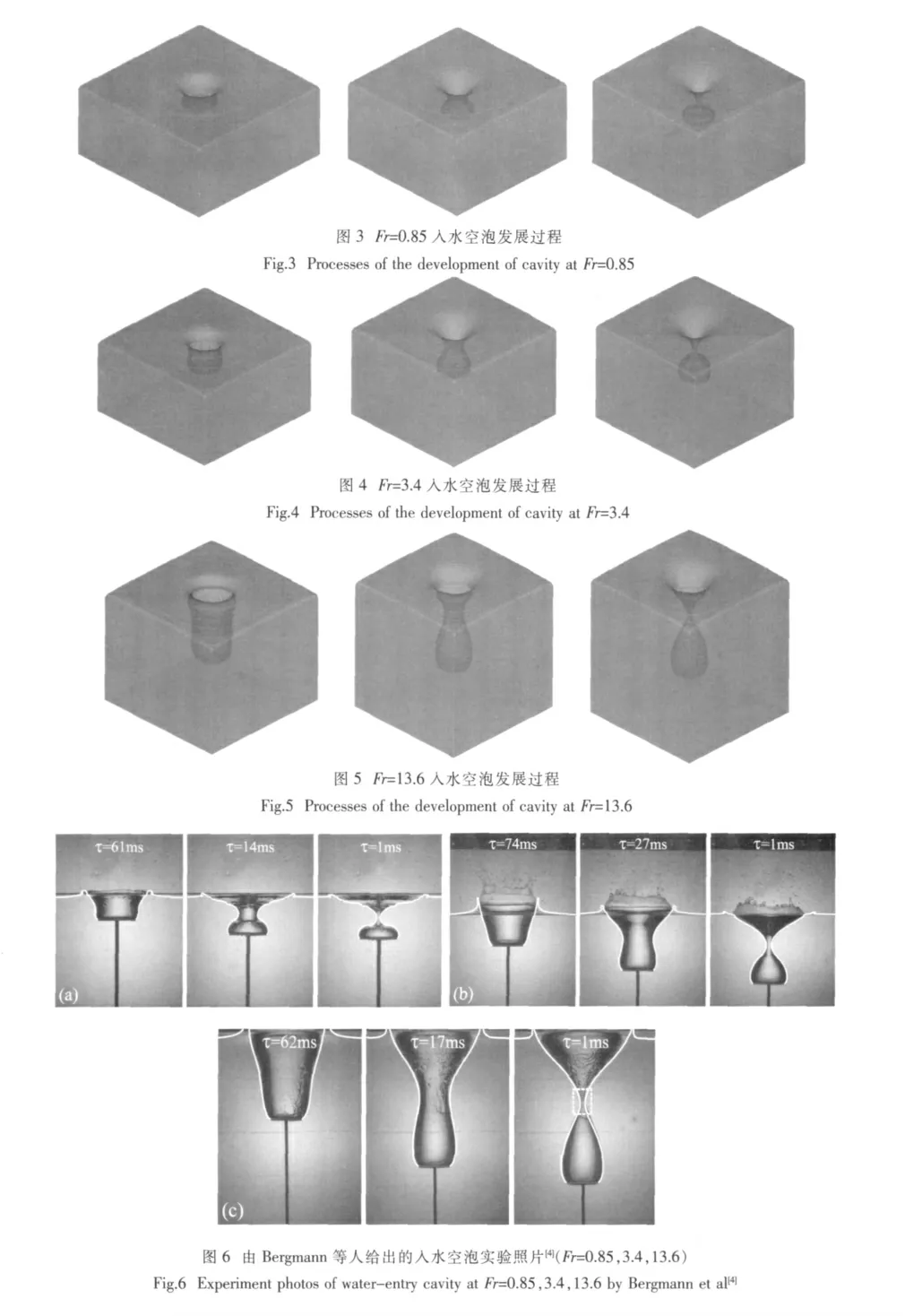
将图3－5与图6的相应试验结果相比较，可见：在Fr=0.85工况下由于Froude数相对较小，入水空泡在离水面不远处立即闭合，这与实验过程相一致。随着Froude数的增大，入水空泡的闭合深度逐渐增加。数值模拟结果也复现了这一现象。总体上看，数值模拟结果与试验结果较为吻合。图5的数值模拟结果中，液面附近未形成如实验照片图6（b）所示的冠状结构，也未见液面的破碎、液滴的飞溅现象。原因可能是在本文所使用的单机计算性能的限制下，数值模拟中圆盘的半径的格子密度不够大，还不足以捕捉到液面附近精细的拓扑结果变化。

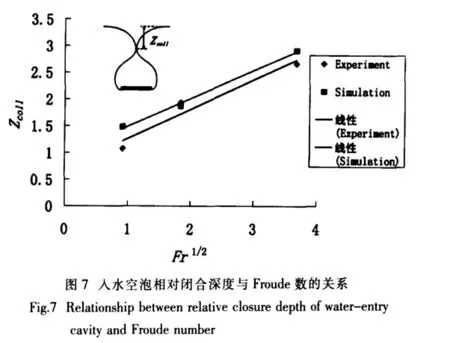
图7给出了本文计算的入水空泡闭合时空泡相对闭合深度Zcoll/R与Froude数平方根的关系，并将计算结果与Bergmann等人[4]的实验结果进行了比较，其中Zcoll为入水空泡闭合深度。

从图7可见，本文数值模拟得到的空泡相对闭合深度Zcoll/R与Froude数平方根基本呈线性关系，这与实验结果相一致；同时，其斜率也与实验结果拟合得到的斜率相一致。计算得到的空泡相对闭合深度总体上比实验值略为偏大，可能的原因是在模拟过程中，由于单机计算条件的限制，计算域的尺寸不够大而产生的影响。

4 结论和展望

本文尝试采用格子Boltzmann单相自由面模型数值模拟了圆盘垂直等速入水空泡的发展过程；计算结果给出了不同Froude数下圆盘入水空泡随时间的变化过程；研究了入水空泡相对闭合深度与Froude数之间的关系；数值计算结果与相关实验结果吻合较好。表明格子Boltzmann单相自由面模型可以用来研究出水空泡的发展过程问题，为其模拟更为复杂的自由面流动问题打下了基础。

[1]陈九锡,颜 开.用MAC方法计算平头物体垂直等速入水空泡[J].空气动力学学报,1986,4(1):47-55.

[2]Kleefsman K M T,Fekken G,Veldman A E P,et al.A Volume-of-Fluid based simulation method for wave impact problems[J].Journal of Computational Physics,2005,206:363-393.

[3]龚 凯,刘 桦.圆盘垂直入水的SPH数值模拟[C].成都:第二十届全国水动力学研讨会文集,2007.

[4]Raymond Bergmann,Devaray van der Meer,Gekle,et al.Controlled impact of a disk on a water surface:Cavity dynamics[J].Journal of Fluid Mechanics,2009,633:381-409.

[5]Luo L S.The lattice-gas and lattice Boltzmann methods:past,present and future[C]//Proceeding of International Conference on Applied Computational Fluid Dynamics.Beijing,China,2000.

[6]Nils Thürey.Physically based animation of free surface flows with the Lattice Boltzmann Method[D].PHD Thesis,University of Erlangen-Nuremberg,2007.

[7]Qian Y,d’Humières D,Lallemand P.Lattice BGK models for Navier-Stokes equation[J].Europhysics Letters,1992,17(6),479-484.

[8]汤 波,李俊峰等.带自由面流体运动的单相格子Boltzmann方法模拟[J].清华大学学报（自然科学版）,2008,48(11):34-360.

[9]Buick J M.Lattice Boltzmann methods in interfacial wave modeling[D].PHD Thesis,University of Edinburgh,U.K.,1997.

[10]Yu D Z,Luo L S,Wer S Y.Viscous flow computation with the method of lattice Boltzmann equation[J].Progress in Aerospace Sciences,2003,39:329-367.