法线垂距在确定点与线元关系中的运用探讨
2010-04-19杨双富
杨双富
(云南一九八煤田地质勘探队,云南昆明 650208)
法线垂距在确定点与线元关系中的运用探讨
杨双富∗
(云南一九八煤田地质勘探队,云南昆明 650208)
基于线路中线的线元组合,提出了利用法线垂距确定点与线元位置关系的方法。
线路中线;线元;几何参数;主点;曲率半径;法线垂距
1 前 言
目前,在线路工程中,尽管线路中线形式多种多样,但绝大部分都是由称之为线元的直线段、圆曲线段和缓和曲线段,按照一定要求排列组合而成的首尾相接的曲线链。每个线元的起点及止点这两个端点称为线路的主点,线元的几何参数有起点的里程、坐标、曲率半径、切线方位角,止点的曲率半径,以及线元长度。由任意点的坐标,根据线元的几何参数确定其在既定线路中的里程和边距称为反算,而反算的第一步,也是重要的一步——即确定点与线元的位置关系。为能快速准确地解决这一问题,文中提出了利用法线垂距确定点与线元位置关系的方法,并给出实现这一方法的伪代码。
2 数学模型
2.1 法线垂距确定点与线元位置关系
如图1,任取一线元 AB,其起点的坐标为(x0,y0)、切线方位角为F0,其止点的坐标为(xn,yn)、切线方位角为Fn,在线元附近任取一点P,其坐标为(x,y)。分别以线元起、止点为坐标原点,以指向线路前进方向的切线为X轴,以垂直于X轴且指向线路前进方向右侧的法线为Y轴,建立如图中所示的X′AY′坐标系和X″BY″坐标系,P点到起点法线的距离d0(简称起点法线垂距)、P点到止点法线的距离dn(简称止点法线垂距)分别为X′AY′坐标系的X′坐标值、X″BY″坐标系的X″坐标值。通过分析,不难得出以下结论:

2.2 点到法线的垂距
在图2中,AD为过线元起点A且指向线路前进方向右侧的法线,根据二维坐标平移旋转公式有:

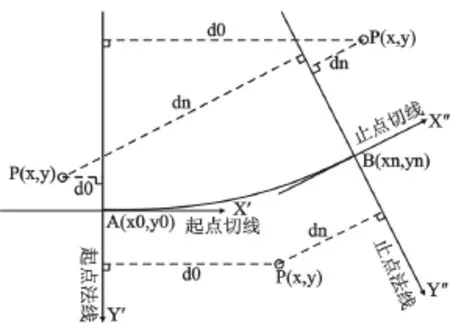
图1 点与线元位置关系

图2 点到直线的距离
3 伪代码及运用实例
3.1 伪代码
假设某线路的中线由n个线元组成,任意点P的坐标为(x,y),则实现利用法线垂距确定点与线元位置关系的算法伪代码如下:


3.2 实现算法的主要程序


3.3 运用实例
如图3及表1所示,某段线路的中线有直线+完整缓和曲线+圆曲线+非完整缓和曲线+直线5个线元组成,直线段起止点的曲率半径无穷大用1.00E+45(即1045)代替(既能满足精度要求,又避免计算中产生溢出错误),线元向左偏转的长度为负值,表1最后一行为最末一个线元的止点,其坐标、切线方位角可按文献[2]方法得到。起点切线方位角按整数为度值,小数点后第一、二位为分值,第三、四位为秒值的方式录入。表2为线路附近的17个点利用法线垂距确定其所在线元的结果。

图3 法线垂距确定点与线元位置关系运用实例略图

线元参数表 表1
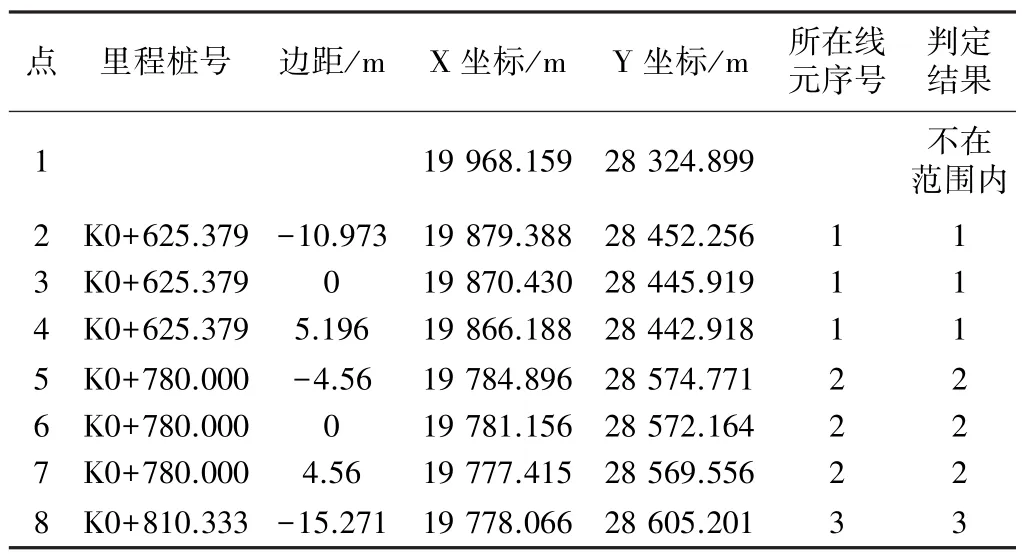
法线垂距确定点与线元位置关系结果 表2
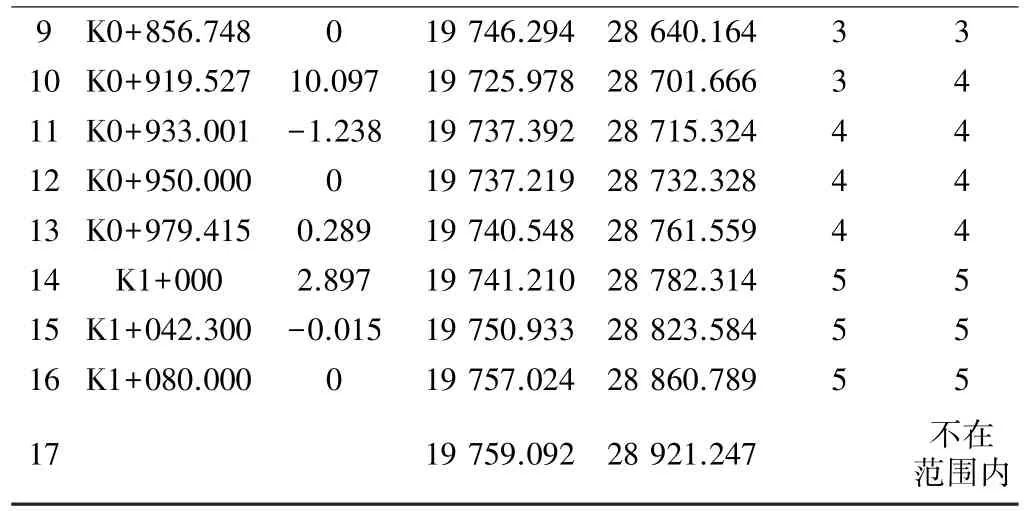
续表2
4 结 语
(1)文中提出的方法,经实践证明,可以方便快速地确定点与线元的关系,适合编程计算。
(2)值得注意的是在回头曲线、匝道范围内可能存在一个点位于多个线元内的情况,文中仅给出了满足式(1)的第一个线元序号,期待广大读者对此进行探讨,提出一个切实可行的解决方案。
[1]秦世伟,陈小枚.快速确定交通路线加桩的简易方法探讨[J].测绘通报,2001(1):14~15
[2]李全信.线路测量中的正反算问题及应用[J].测绘通报,2006(2):36~38
In Determining the Normal Vertical Distance Between Point and Line Segment in the Use
Yang ShuangFu
(198 coal geological exploration teams in Yunnan Province,Kunming 650208,China)
Based on combination of line center line of the line element is proposed to determine the use of normal vertical distance between point and line segment position method.
line midline;line element;geometrical parameter;the main point;curvature radius;normal vertical distance
1672-8262(2010)04-120-03
P20
B
2009—12—21
杨双富(1967—),男,高级工程师,主要从事工程测量工作。
