高层建筑沉降观测相关问题探讨

田海勇

(洛阳规划建筑设计有限公司，河南洛阳 471000)

高层建筑沉降观测相关问题探讨

田海勇∗

(洛阳规划建筑设计有限公司，河南洛阳 471000)

高层建筑沉降观测经常会出现基准点变化和观测点“上升”现象，对这些问题的分析与处理是否得当，将直接影响到对建筑物沉降变形的分析判断。本文结合实际，针对洛阳市的情况就这一问题进行分析论述，提出了处理这类问题的具体方法。

高层建筑；沉降观测；基准点；稳定性；观测点；整体下沉；数据处理方法

1 引 言

近年来，随着城市的快速发展，高层及超高层建(构)筑物越来越多[1，2]，高层建筑沉降观测问题越来越受到重视。由于各种原因，很多地方开展高层建筑沉降观测的时间都不长，资料和经验不足，对高层建筑沉降观测的研究需要不断地深入。由于各地的情况不同，沉降观测又是涉及多个学科领域比较复杂的一项工作，需要研究和探讨的问题很多，因此，在一些具体问题处理上，会表现出明显不同的地方特色。本文针对洛阳市的具体情况，结合笔者多年的经验，对高层建筑沉降观测中出现的一些特殊情况进行分析探讨，提出了具体的处理方法。

高层建筑一般采用桩基础、筏板基础或箱基础，且荷载较大，高层建筑施工将给其自身及周边建筑群体带来复杂的形变影响。对高层建筑开展变形监测的目标一般有两个:一是对高层建筑本身进行监测，二是对基坑及周边建筑群进行监测[3，4]。洛阳市根据其特殊的城市地理环境和地质构造，重点开展了对高层建筑主体的沉降观测。

根据历年来的经验，洛阳市高层建筑沉降变形的幅度比较小(总沉降量10 mm～30 mm)，沉降观测一般采用二级的观测精度，由于涉及地质条件以及建设成本等原因，无法建立高标准的基岩点，在沉降量不大的情况下，基准点的稳定性就成为一个突出的技术问题，经常造成建筑物出现不正常的“上升”[5]现象，对这一问题的处理，会直接影响到对建筑物变形情况的判断是否得当。

2 几个应用问题

2.1 沉降观测关注的对象

我们通常最关心的是建筑物最大沉降量以及是否均匀下沉，建筑物从施工到使用后各个时期的沉降量变化是不同的，因各地的地质构造情况不同和各个时期时间性不同，设计要求也不同。能够及时反映这种变化，是设计和施工需要关注的问题。

大型和高层建筑的沉降观测的内容主要是测定建、构筑物均匀沉降和不均匀沉降，包括地面沉降观测和建筑物沉降观测。对于高层建筑物沉降观测的任务，是周期性地对观测点进行重复观测，求得其在两个观测周期间的高程变化量。高层建筑的沉降变形按其类型来区分，可以分为静态变形和动态变形。

我们通常说到的沉降观测精度的确定是指观测中误差的确定，绝对沉降(如沉降量、平均沉降量等)的观测中误差，对于特高精度要求的工程可按地基条件，结合经验与分析具体确定；对于其他精度要求的工程，可按低、中、高压缩性地基土的类别，分别选择±0.5 mm、±1.0 mm、±2.5 mm。相对沉降的观测中误差[3，4]，根据规定，如果观测目的是为了使变形值不超过某一允许的数值而确保建筑物的安全，则其观测的中误差应小于允许变形值的1/10～1/20。我国建筑设计部门以允许倾斜值的 1/20作为监测的精度指标[5～7]。

沉降观测周期的确定，在国家规范的基础上，各地根据实际情况制订了地方标准，洛阳市规定:高层建筑物的施工出了地面，即到了零高度后，每施工1～2层要观测一次，直至封顶。封顶后的第一年每季度观测一次，第二年每半年观测一次，第三年开始每年观测一次，直至沉降停止。如果发生沉降异常，应酌情增加观测次数。

2.2 高程基准点的设置问题

(1)地质条件与埋深

一般来说，高层建筑物的沉降观测多采用精密水准测量、液体静力水准测量、微水准测量、三角测量和地面摄影测量的方法。其中，精密水准测量方法最为简单直接，成本相对低廉，是目前最常用的方法。

采用精密水准进行沉降观测时，需要有稳定可靠的基准点，最理想的情况是基准点设在基岩上。由于城市大多建在平地，一般远离山体或者岩体位置很深，建造基岩点不方便，而且成本很高，对于高层建筑密集的城市来说，建造大量基岩点是不现实的。

洛阳市只有龙门山可以设置浅埋基岩点，但龙门山距市中心区有 7 km之远。洛阳市区基岩离地表深度一般在200 m以上，设置基岩点非常困难。1985年在涧西区按地质构造设置了分层标组，包括9个分层标，全部采用内外双层钢套管，主标为1＃标，埋设于区域结构致密的第三纪粘土岩层面上，以此标作为该标组的相对稳定点，终孔深度 167.42 m，其他分层标终孔深度为1.3 m～63.0 m不等，鉴别孔225.81 m，未打穿第三纪粘土岩，如表1所示。从1987年到2004年，洛阳市进行了7次城市地面沉降观测，分层标与龙门山基岩点经联测，主标在1991年第4次观测时，为上升1.8 mm，其他6次均稳定，副标随深浅不同有变化，如表2所示。

分层标埋设情况 表1

1993年～2004年分层标观测情况 表2

根据有关资料，洛阳市市区主要位于洛河、涧河和伊河的一、二级阶地上，阶地主要由河流冲积或洪积形成。洛河以北城区二级阶地黄土厚度平均约20 m；临近洛河为一级阶地，地势较低，黄土厚度平均约5 m～8 m。洛河以南区域为一级阶地，部分区域为坡洪积山前平原，黄土厚度平均约3 m～5 m。黄土下地质情况较为复杂，分层较多，砂层、卵石层间隔混合分布，形成年代不同。一般认为砂卵石层为稳定的持力层，可压缩性极小。

洛河二级阶地黄土层土质比较稳定，一般含水较少，可压缩性和膨胀系数均比较低，适合建筑。相关资料显示，该区域湿陷性土层厚度约 1 m～2 m，位于地表下8 m～10 m的深度。根据洛阳市历年来对城市地面沉降的研究，近10年来城市地面平均沉降10 mm～30 mm，年平均下沉1 mm～3 mm，主要为城市地下水位下降引起。

洛阳市对基准点埋设要求为埋深12.5 m或达到砂卵石层。按一般黏土进行单桩承载力验算[8]:直径300 mm、长12.5 m混凝土桩自重为2.2 t，来自侧面的摩擦力为 23.5 t，底部端阻力为 7.1 t，合计 30.6 t。显然，桩自然下沉受到的阻力要远大于干桩自重，在没有外部荷载的情况下，理论上桩受力是稳定的，应该不会下沉。黄土层薄的地方，桩埋深可达到砂卵石层(深度3 m～8 m)，持力效果明显，稳定性更好。根据表2数据，结合历年来对建筑场地基准点稳定性的检测情况，将新埋基准点与分层标、早期埋设的城市高等级水准点、基础较深的稳定建筑等进行联测，对不同埋设深度的基准点，结果均与理论相吻合，桩位稳定性都很好，2年～3年内自然沉降量一般小于3 mm，个别沉降量大一点的也只有5 mm左右。表3列出了近年来部分工程基准点稳定性检测结果。

基准点稳定性检测结果 表3

在早期埋设基准点时，没有进行孔底清理和夯实，而且首次观测在基准点埋设后15天进行，混凝土没有完全凝固，部分基准点出现了下沉现象，尤其在基准点设置后1个月～3个月第一、二次检测时表现比较明显，下沉量在1 mm～2 mm左右，之后个别点位出现微小下沉量往往伴随现场变化及周围场地的扰动，大部分点位后期稳定。后来做桩时，用特制的夯锤对桩孔进行了底部处理，并提前1个月～2个月埋设基准点，基准点稳定性明显提高，如表4所示。

孔底处理后基准点稳定性检测结果 表4

(2)埋设位置

基准点与沉降观测点之间的距离是一个值得关注的问题。通常情况下，测站高差中误差采用S05水准仪观测时可达到±0.13 mm，采用S1水准仪观测时可达到±0.15 mm[3]。要保证控制点到观测点高差中误差小于±0.5 mm的精度，采用S05时测站数不能多于14站，采用S1时测站数不能多于11站。由于受各种因素的影响，实际作业时，能够有效保证的测站精度一般在±0.15 mm～±0.2 mm之间，考虑到精度储备和其他因素，测站高差中误差按±0.2 mm计算，实际作业时附合水准路线长度以不超过12测站为宜，最弱点距离控制点距离以不超过6测站为宜。据此推算，平均视距按 35 m计算，基准点距离沉降观测点应不超过420 m。因此，基准点应尽可能设在距离施工场地附近约500 m范围之内。如果距离太远，误差积累过大，会掩盖实际沉降量。

根据洛阳市的实际，筏板基础的深度一般为 6 m～10 m，加上挤密桩的深度最深不过 20 m左右，基坑周围扰动范围很有限，基准点设在场地外围 30 m～100 m的位置是比较合适的。这样既能够保证基准点的稳定性不受建筑施工影响，又能够便于使用和保存。

2.3 工作基点的设置问题

通常情况下，建筑场地内不适合埋设永久性的基准点，基准点只能设在场地外围，有时候距离观测目标距离较远，联测路线较长，造成误差累积过大，利用起来很不方便。因此，在建筑场地内布设一定的工作基点很有必要。工作基点为临时的固定点，埋设规格比基准点低，在短期内相对稳定。在施工阶段，观测周期一般较短，通常不超过10天，工作基点在3个～5个观测周期内变化较小，进行稳定性检查后，可以代替基准点作为控制点使用。这样，可以有效节约观测成本，又能保证观测质量。

工作基点的设置应同时考虑观测方便和构网的图形强度。高程控制网应由基准点和工作基点组成独立网，图形强度以均匀分布覆盖所有观测点为宜，各水准路线测站数应均匀并不超过12测站。工作基点应1月～2月全面复测一次，作业过程中如发现点位不稳定，应随时复测。

进行沉降观测时，可就近利用基准点和工作基点，组成线路时应尽量简化，以多线路、少测站为宜，沉降观测路线可不构成整体网进行平差，按独立的附合线路分别计算。

3 基准点的稳定性判断

3.1 基准点稳定性分析

基准点只要不建在基岩上，就会存在或多或少的下沉现象。但由于没有可靠的参照点，基准点绝对下沉量是无法判定的。通过点与点之间的高差变化，可以判断基准点是否相对稳定。当2个基准点之间高差绝对值变大时，一定是较低的点相对下沉了；当2个基准点之间高差绝对值变小时，则一定是较高的点下沉了。比如:A到B点原高差为hAB＝HB－HA＝1.000 m，检测高差hAB＝1.010 m，高差绝对值变大，可以判定A点下沉；同理，如果检测高差hAB＝0.990 m，可以判定B点下沉。通过这种方法，基本可以判断出控制网中各个点位的相对稳定情况，并可以推断出相对稳定的点位。如果在判断基准点稳定性时出现了不符合逻辑的反常现象，比如:A、B、C三点联测后，由A、B点变化判定B点下沉，由B、C点变化判定B点上升(或C点下沉)，A、C点比较结果又都稳定。这种情况应考虑观测粗差影响，核对记录、计算，及时进行返工复测，剔除粗差[6]。

由于基准点之间有一定的距离，相互扰动的情况很少，一般情况下，出现同时下沉的几率很小。按照要求，在对控制网进行定期复测时，可以对基准点稳定情况进行分析和预测，必要时可以增加复测次数。通过不断修正基准数据，避免因基准点下沉造成的数据断链。

通过对基准点稳定性进行分析，找出相对稳定的基准点并把该点作为拟稳点，以拟稳点为起算基准，对整个控制网(包括基准点和工作基点)重新进行平差计算，计算结果作为修正后新的高程基准。

3.2 基准点整体下沉情况分析

有时候会出现建筑物整体“上升”现象，对基准点进行稳定性检查后，仍然不能排除沉降观测点“上升”现象。那么，建筑物会不会整体“上升”呢?

根据相关理论，大型建筑物由于自身荷载较大，在不卸载的情况下对地基始终是处于一种压缩状态。建筑物随着地基土的被压缩，呈现下沉，下沉的过程因土质、地质构造、地下水状态、建筑结构、施工方式以及基坑周围建筑物分布、荷载变化等不同因素影响，会出现各种复杂的变化。有连续稳定下沉，有阶段性下沉，有先快后慢的，有先慢后快的，有快慢交互出现的，需要具体问题具体分析。

建筑物“上升”的情况，只在有条件的情况下出现。这些条件主要有以下3个方面:

(1)建筑物本身荷载较小，且荷载稳定。当该建筑位于其他大型建筑附近，地基被扰动，附近大型建筑在下沉的过程中，对周边建筑的地基产生较大的作用，随着地基的上升，建筑物被相应地“拱起”。

(2)建筑物荷载减小，地基发生回弹。

(3)地基为膨胀土，且土层较厚，地下水位升高时，对地基产生向上的应力，地基遇水后发生膨胀，将地表建筑“抬起”。

对于洛阳市的情况，地表黄土较薄且稳定性好，膨胀系数低，城市地下水位处于逐年下降的状态，洛河周边随着洛河季节水位的变化，部分区域地下水位略有回升，但幅度不大，周期很短。地基上升的情况概率很低，根据地质部门提供的信息，建筑物上升的情况主要是卸载后的地基回弹影响。

另外需要说明的是，建筑物沉降时不会因为局部微小的下沉就造成另一部分被所谓“挑起”。一般情况下，建筑物沉降量很小，一个观测周期内沉降量最多只有几毫米，整个观测期间，总的下沉量一般也不超过20 mm，而结构弯曲变形的允许幅度要远大于这个数值，加上有巨大的荷载作用，结构反弹的力度不会超过结构变形的幅度。

根据以上所述，沉降观测中出现建筑物“上升”的现象是不正常的，其原因主要是由于基准点下沉所引起，由于基准点下沉幅度超过了建筑物沉降幅度，掩盖了建筑物正常的下沉量。例如:某工程位于洛河北岸，共4栋高层，埋设基准点8个，埋深6 m～7 m达到砂石层，建筑增高4层、进行第3次沉降观测时，发现建筑物整体“升高”1 mm，而基准点相对稳定。把基准点与最初联测的附近城市高等级水准埋石再次联测，结果是8个基准点相对于城市高等级水准点整体下沉2 mm。将这2 mm考虑进去后，建筑物实际沉降量为1 mm。该项目经过后期多次检测，均未再发现基准点不稳定和建筑物整体“上升”现象。

当出现建筑物“上升”的现象时，应从分析基准点稳定性着手，采取各种必要的手段，剔除因基准点下沉造成的判断失误。主要的技术手段有:合理设置基准点、增加基准点数量、加大基准点埋设深度、加强对基准点稳定性检验的力度、采用合适的数据处理方式等。

4 特殊情况的数据处理方法

基准点和沉降观测点出现“上升”的异常情况时，除了采取检查原始数据和复测的方法外，在数据处理上可采用拟稳分析的方式对观测数据进行修正。

拟稳分析的基本思路是:建筑物不可能上升，所有观测点均会处于不稳定的状态，没有严格意义上的固定点可以作为起算依据，在所有观测点中必然有相对稳定的点，包括基准点和沉降点在内的所有观测点相对于整个地表而言，其绝对下沉量是未知的，沉降观测对象为相对独立的主体，我们更关心建筑物本身变形以及建筑物与地基的关系变化，这种关系变化与区域性的地表下沉没有严格意义上的关系，也就是说只需要关注相对下沉量及其关系。

因此，可以采用以下的数据处理的方法和步骤:

(1)基准点拟稳分析。可采用高差比较法，逐个分析，找出相对稳定的基准点，将该点确定为拟稳点。也可以采用平差计算的方法，先任意指定一个基准点为起算点，平差后与原高程值比较，“上升”最大的基准点即为拟稳点。以拟稳点为起算点，对复测的控制网进行平差，得到一组拟稳平差后的控制点成果。

(2)沉降量计算。根据拟稳平差后的控制点成果，计算沉降观测点高程，并与原高程值进行比较。如果所有沉降观测点均没有“上升”，或者“上升”幅度小于2倍测站高差中误差(即＜0.5 mm)，并且“上升”的点数量不多，可以认为选定的拟稳点没有沉降。其中，“上升”的点可以认为是测量误差所致，剔除误差，将其本次的沉降量修正为0即可[5]。

(3)拟稳点沉降量计算。根据拟稳平差后的控制点成果，计算沉降观测点高程，并与原高程值进行比较。如果有大量沉降观测点“上升”，或者“上升”幅度≥0.5 mm，应考虑拟稳点存在下沉。拟稳点的下沉量根据观测点中“上升”幅度最大的点来确定。将最大“上升”值作为拟稳点的下沉量，修正所有观测点的高程，重新计算高程和下沉量，填写新的控制点成果表和沉降观测成果表，并作为本次最终成果。

(4)数据处理过程中的分析资料和计算资料，作为原始资料保存。在后期的观测过程中，均采用修正后的成果。如果再次发生类似情况，采用同样办法处理。

(5)在数据处理的过程中，应填写相关的说明，详细说明基准点、沉降观测点的异常情况，以及可能的原因分析、处理方法、处理结果等，并提出更改措施、注意事项等供后期工作中参考。

工程实例:某高层建筑在施工过程中载荷增加2层的情况下，观测数据反映出建筑物“上升”现象，现场调查后排除了其他异常情况，判定为基准点整体下沉并伴随发生不均匀变化。部分点位的数据处理过程如表5～表7所示。

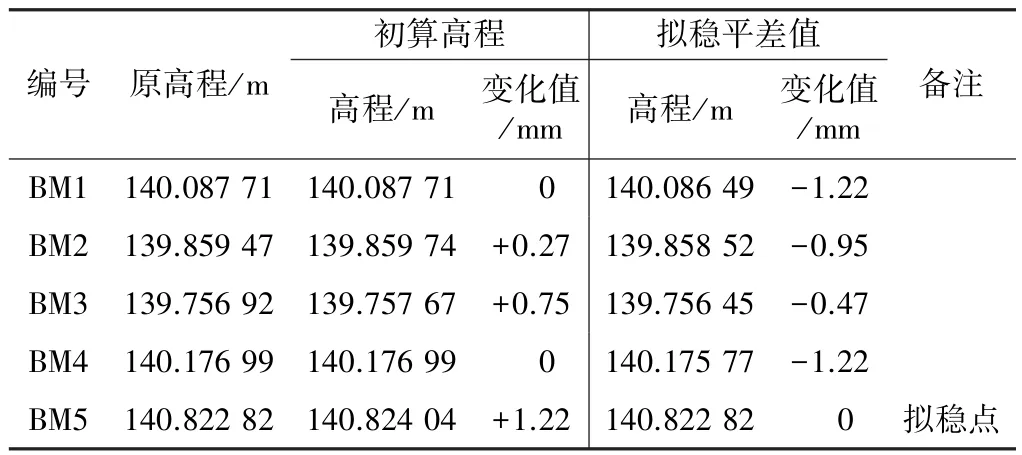
基准点拟稳分析及数据处理 表5

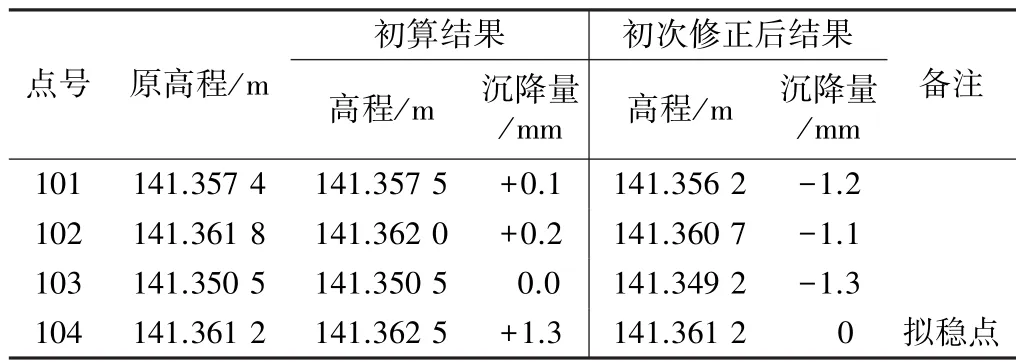
沉降观测点拟稳分析及数据处理 表6

基准点数据修正 表7

5 沉降观测需要注意的问题

(1)基准点和工作基点的埋设位置、深度应根据场地条件、地质条件合理设计。

(2)观测路线要选择，测站数要控制。选择观测路线和观测方法时，应以提高测站观测精度、减少设站数为主，减少影响精度的不必要程序和环节。

(3)观测精度需要重点考虑。平差本身不能提高精度，只是一种数据处理的手段。最弱点精度与观测精度和距离控制点的距离有关，同时与网形和平差方式也有一定关系。改善网形和选择合适的平差方式，可以使精度分配更合理、更均匀。

(4)出现异常情况时需要综合分析，点位“上升”时应综合考虑各种因素，首先分析是否有“上升”的客观条件，排除其他因素后再重点考虑基准点下沉情况。

(5)应尽可能利用较少的工作基点，观测尽可能多的沉降点。

(6)沉降分析必须有可靠的依据，判定建筑物沉降异常变化尤其是上升必须有充分可靠的依据，理论上应有合理性，数据应相互印证。

[1]韩正，杜海霞，龙飞等.高层建筑沉降观测及其数据分析[J].城市勘测，2009(1)

[2]刘忠华，吕长广.建筑物沉降观测的有关问题及解决方案[J].城市勘测，2009(1)

[3]JGJ8－2007.建筑变形测量规范[S].

[4]GB50026－2007.工程测量规范[S].

[5]岳建平，田林亚.变形监测技术与应用[M].北京:国防工业出版社，2007，7－12，140～146

[6]陈永奇.变形观测数据处理[M].北京:测绘出版社，1988，5～14

[7]黄声享，伊晖，蒋征.变形监测数据处理[M].武汉:武汉大学出版社，2003，30～40

[8]JGJ94－2008.建筑桩基基础规范[S].

The Interrelated Problems of Settlement Observation for Highrise Building

Tian HaiYong
(Luo Yang Planning＆Architectural Design Co.，Ltd.Luo Yang 471000，China)

The change of standard and object raising was impersonal for the highrise building settlement observation. This problem need to analyze，to process，the method influence result.According to the practice in Luo Yang，means was appeared.

High－rise Building；Settlement Observation；DatumPoints；Stability；Observation Points；Entire Sinking；Data Analyse

1672－8262(2010)05－147－05

TU196.2

A

2009—09—30

田海勇(1966—)，男，高级工程师，主要从事城市测量、工程测量、变形测量等技术应用与研究工作。