隔震结构地震响应的简化计算方法*
2010-04-15沈金生李荣华
沈金生 刘 杰 李荣华
由于在隔震结构中,隔震系统与上部结构的阻尼特性截然不同,整个结构组成一个典型的非比例阻尼体系,这使得结构的动力响应分析具有相当的难度,国内外学者也将其作为一个特殊的课题加以研究。本文采用分区瑞利阻尼方法分解阻尼矩阵,用拉普拉斯变化及其逆变化解耦运动方程,将双自由度隔震建筑地震响应最大值表达为位移反应谱形式,且具有较高的精度。
1 隔震体系运动方程及非比例阻尼矩阵的处理
一般层剪切模型隔震体系的运动方程为:
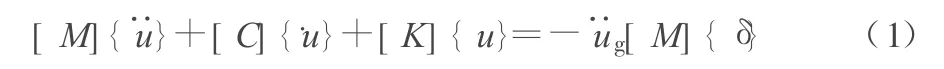
其中,[M],[C],[K]分别为隔震体系的质量、阻尼、刚度矩阵;{¨u},{﹒u},{u}分别为各质点相对位移、速度、加速度向量。 采用分区瑞利阻尼模型,非比例阻尼矩阵分解为:

其中,[C0]为经典瑞利阻尼矩阵;[Cr]为非比例阻尼的余项阻尼矩阵。

其中,αs,βs,αb,βb分别为上部结构和隔震系统的子结构瑞利阻尼比例系数。
2 隔震层位移响应和上部结构底层最大层间剪力位移反应谱计算方法
对方程(1)两边进行零初值得拉普拉斯变化和拉普拉斯逆变化,根据隔震结构的动力特性,只考虑前两阶振型的贡献,隔震结构隔震层的位移表达式为:

上部结构底层最大层间剪力表达式:

其中,μ为隔震建筑上部结构底层剪力修正系数,上部结构为混凝土框架体系的非比例阻尼隔震建筑上部结构底层剪力修正系数μ的建议公式:

其中,N为结构的层数(包括隔震层),当N≥10时,取 N=10。
3 工程算例
为验证本文的非比例阻尼隔震结构的反应谱计算方法的可行性,选取3个实际的隔震工程作为算例(见表1)。隔震层阻尼比ξb=0.15,上部结构阻尼比ξs=0.05,为了使按本文的非比例阻尼隔震结构的反应谱计算方法能够和时程分析法的计算结果对比,选用 EL-Centro波、Taft波、NorthRidge波的位移反应谱,加速度峰值小震时调幅至0.7 m/s2,大震时调幅至4.0 m/s2,相当于8度区(0.2g)设防烈度。在各种阻尼状况下,3条地震波的位移反应谱由作者编写的Matlab程序计算求得(见图1)。

表1 隔震工程的刚度和质量

对表2,表3中的隔震层位移和上部结构底层层间剪力计算结果及误差分析,隔震结构在常用的阻尼状态下,用本文的位移反应谱计算方法得出的结果和时程分析方法计算的结果进行对比,隔震层位移误差和上部结构底层层间剪力的误差分别为:工程1为0.57%和0.35%;工程2为1.03%和0.19%;工程3为0.39%和0.33%。均能满足工程精度要求且计算简便。

表2 隔震层计算位移 mm

表3 上部结构底层层间剪力 kN
4 结语
根据隔震层和上部结构的动力参数及场地动力特性,按本文算法,查用位移反应谱,可以简便地计算出上部结构的最大层间剪力和隔震层的最大位移,与现规范采用的概率统计的设计思想相符合且有较好的精度,并能够体现隔震建筑的非比例阻尼特性。
[1] Veletsos A S,Ventura C E.Modal analysis of non-classically damped linear systems[J].Earthquake Eng.Struct.Dyn.,1986(14):217-243.
[2] 施卫星,李正升.基础隔震结构设计反应谱[J].工程力学,1998(S2):115-120.
[3] 杜永峰,杜小妮,赵国藩.用拉普拉斯变换方法求解非比例阻尼隔震结构[J].兰州大学学报(自然科学版),2000,36(11):40-45.
[4] 徐茂义.建筑隔震结构地震反应分析[J].山西建筑,2008,34(32):80-81.
[5] 王亚勇.关于设计反应谱、时程法和能量方法的探讨[J].建筑结构学报,2000,21(1):21-28.
[6] 杜永峰,李 慧.非比例阻尼隔震结构地震响应的实振型分解法[J].工程力学,2003,20(4):89-93.
[7] 周 云,安 宇,梁兴文.基础隔震结构基于位移的设计方法[J].广州大学学报(自然科学版),2002,1(1):75-79.
