弹体脉动压力特征的实验研究

王 娜 ,高 超

(西北工业大学翼型叶栅空气动力学国家级科技重点实验室,陕西西安 710072)

0 引 言

飞行器绕流的非定常特性会导致飞行器表面局部区域产生较大的压力脉动,尤其是与低阶模态的频率范围接近时,有可能导致飞行器结构的疲劳甚至破坏[1]。因此研究飞行器表面受到的脉动压力并进行脉动压力的频谱特性分析对于结构强度设计来说极为重要。目前,在弹体表面大量布置测点,对弹体的表面脉动压力进行精细研究的风洞实验研究还开展得比较少,缺乏关于弹体表面较为完整的脉动压力测量数据及其特征分析结果。关于细长旋成体背部流场的脉动压力实验研究中,C.F.Coe[2]针对尖拱细长旋成体模型和尾部有台阶的尖拱细长旋成体模型,在马赫数 M∞=1.6、2.5、3.0 、3.5,迎角 α=15°、30°、45°、90°的情况下,测量了模型表面 9个特征点的脉动压力,Coe采用无量纲衰减因子参数 f δ/U∞,研究衰减因子与脉动压力之间的关系,得出：衰减因子越小脉动压力越小。但Coe的实验中没有进行跨声速流动的脉动压力测量。Degani[3]研究尖拱细长旋成体模型在雷诺数 Re=17000、26000、35000,迎角 α=0°、30°、40°、50°、55°、60°、70°、80°、85°条件下的非定常流动特性,发现当迎角大于 70°或小于 10°时高频压力脉动会迅速减小,且脉动压力频谱曲线中在迎角α=0°～ 10°之间没有明显的峰值 ,直到迎角 α=20°以后才出现明显的能量峰值。由于在Degani的实验中测点集中分布在圆柱段中部,没有测量旋成体肩部位置处的脉动压力,而此处往往是出现较大脉动压力的地方。马宇[4]等人在低速风洞中,在大迎角条件下测量了尖拱细长旋成体沿轴向的脉动压力,实验发现,压力脉动幅值在迎角α=0°时基本保持不变,直到迎角增大至α=30°后,压力脉动幅值沿着细长旋成体轴向明显增大。笔者针对弹体模型,进行了跨、超声速条件下,弹体表面脉动压力的精细测量,获得了弹体表面测点沿轴向的脉动压力系数、频谱以及相关性系数等,得到了弹体表面脉动压力的频谱特性,和在迎角α=0°条件下,弹体轴向表面各测点脉动压力之间的空间相关性分布规律,以及脉动压力随飞行参数(马赫数M∞、迎角α)变化的基本规律,并对脉动压力重复性实验进行了误差分析。

1 实验模型及设备

实验模型分为圆拱形头部、圆锥段和圆柱段3部分,其外形子午线与沿轴向的脉动压力测点位置如图1(a)所示,圆锥部分由两个斜率不同的圆锥组成,在测点5前方形成台阶区,如图1(b)所示。在0°子午线上,沿轴向布有14个测点。测压孔孔径为φ 3.5mm,动态压力传感器的实际尺寸为φ 2.54mm,外包弹性塑料套,采用表面齐平方式进行安装。

图1 实验模型及测点分布Fig.1 The experiment model and testing points distribution

实验在FD-06跨声速风洞中进行,实验段截面积为600mm×600mm。测试仪器包括动态压力传感器、信号调理仪、数据采集系统等。其中动态压力传感器采用美国Kulite XCL-100传感器,传感器频响大于400kHz,量程为25PSI,灵敏度和线性误差小于±0.1%FS BFSL。动态压力传感器测量所得到的脉动压力信号在传感器尺寸φ 2.54mm区域内的测量值进行空间平均,并近似地将该平均值等效为传感器中心点处的压力脉动。信号调理仪采用了DH-3846A型应变放大器 4台,其线性度误差小于满量程的0.05%。数据采集使用高速采集系统。该实验中,每通道采样频率为200kHz,每通道采样长度为32×1024,采样时间为0.16384s。

2 结果与分析

进行了弹体轴向脉动压力测量,并对典型流动状态进行了纹影录像。实验马赫数为M∞=0.8、0.84、0.86、0.92、1.0 、1.15、2.0、2.5,迎角为 α=-5°、-3°、0°、3°、5°。

考虑到脉动压力主要出现在物面曲率有变化的区域,依据弹体外形特征,将弹体沿轴向的流动区域分为3个典型区域：压缩区、台阶区和膨胀区,如图1(a)所示。下面主要对以上3个典型区域的流动特征进行分析。

2.1 脉动压力与飞行参数的关系

均方根脉动压力代表弹体表面某点脉动压力的总强度,使用来流动压q∞作为均方根脉动压力的无量纲参数,得到脉动压力系数C′p。图2给出了迎角 α=0°时不同马赫数的脉动压力系数沿轴向的变化。可以看出,脉动压力系数总体上随着马赫数增加而降低。当M∞＜1时,脉动压力峰值出现在膨胀区,随着马赫数M∞的增大,脉动压力峰值向后移动,但脉动压力峰值的强度减弱,同时位于膨胀拐角肩部的激波也向后移动(如图3所示)。当M∞≥1时,脉动压力系数明显小于马赫数 M∞＜1的脉动压力系数峰值,当1≤M∞≤1.15时,脉动压力系数峰值出现在台阶区;当M∞＞1.15时,脉动压力系数在压缩区达到峰值。

图2 脉动压力系数随马赫数的变化曲线Fig.2 The coefficient of fluctuating pressure changes with Mach number

图3 纹影录相截图Fig.3 Schilieren image of model

图4 不同迎角脉动压力系数的对比Fig.4 The coefficient of fluctuating pressure at different angle of attack

图4给出了 M∞=0.8和 M∞=1.15情况下,不同迎角脉动压力系数沿轴向的变化曲线。可以看出,总体上,脉动压力系数在弹体表面曲率变化较小的位置基本上不随来流迎角的改变而变化,但是在弹体表面特征位置处,尤其在膨胀拐角肩部,脉动压力系数随着迎角的改变而变化较大,这是因为弹体表面脉动压力主要与弹体外形型面曲率有关,在来流迎角的变化不大的条件下,由于弹体表面曲率变化不大,对脉动压力系数的影响有限,而膨胀拐角处的弹体表面曲率变化相对较大,体现为膨胀拐角肩部的脉动压力系数随着迎角的变化而变化。当M∞=0.8时,脉动压力系数最大值均出现在膨胀区;在膨胀拐角肩部,脉动压力系数峰值随着迎角的绝对值增加而降低。当M∞=1.15时,脉动压力系数最大值均出现在台阶区,且基本不随迎角变化;压缩拐角及膨胀拐角肩部的脉动压力系数随着来流迎角的增加而增大。

2.2 脉动压力的频谱特性

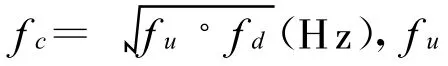
在不同马赫数条件下,各个测点的功率谱能量密度峰值所对应的频率用主频表示,特征频率表征了主频所在频率区间的平均值。图5给出了不同马赫数下各测点的主频对比曲线,表1给出了不同马赫数条件下的特征频率。可以看出,跨声速时,绕流的特征频率出现明显的中频特征,随着马赫数增加,特征频率增大;在M∞＜1.0的情况下,在膨胀拐角位置的主频表现出很强的低频特征。当马赫数M∞＞1.15时,表现为宽带湍流频率特性。

图5 不同马赫数下主频对比曲线Fig.5 The main frequency distribution atdifferent Mach number

表1 不同马赫数下特征频率列表Table 1 The characteristic frequency at different Mach number

图6给出了马赫数M∞=0.8、1.15、2.5,迎角 α=0°时弹体外形的3个特征位置的1/3倍频谱曲线。可以看出,能量密度的幅值与典型位置处脉动压力系数相对应。在脉动压力系数出现峰值的区域,能量密度较高。当频率大于12kHz时,能量密度迅速衰减。亚、跨声速来流情况下,能量密度峰值出现在6～10kHz处。当M∞=1.15时,弹体的压缩区及台阶区的能量密度明显较高。超声速来流情况下,能量密度峰值出现在低频区域,但能量密度普遍较小,对应着脉动压力系数峰值出现的压缩区,能量密度峰值仅为40Pa2/Hz。相应的理论表明,压力脉动现象的产生主要是由于流动发生了分离、激波振荡,以及层流转为湍流造成的,分析弹体表面压力脉动的频谱特性,可以看出,弹体表面脉动压力的频谱特性具有湍流脉动能量的峰值出现在低频区域,高频区域幅值较低;激波振荡明显表现出低频区域幅值较高的特点。

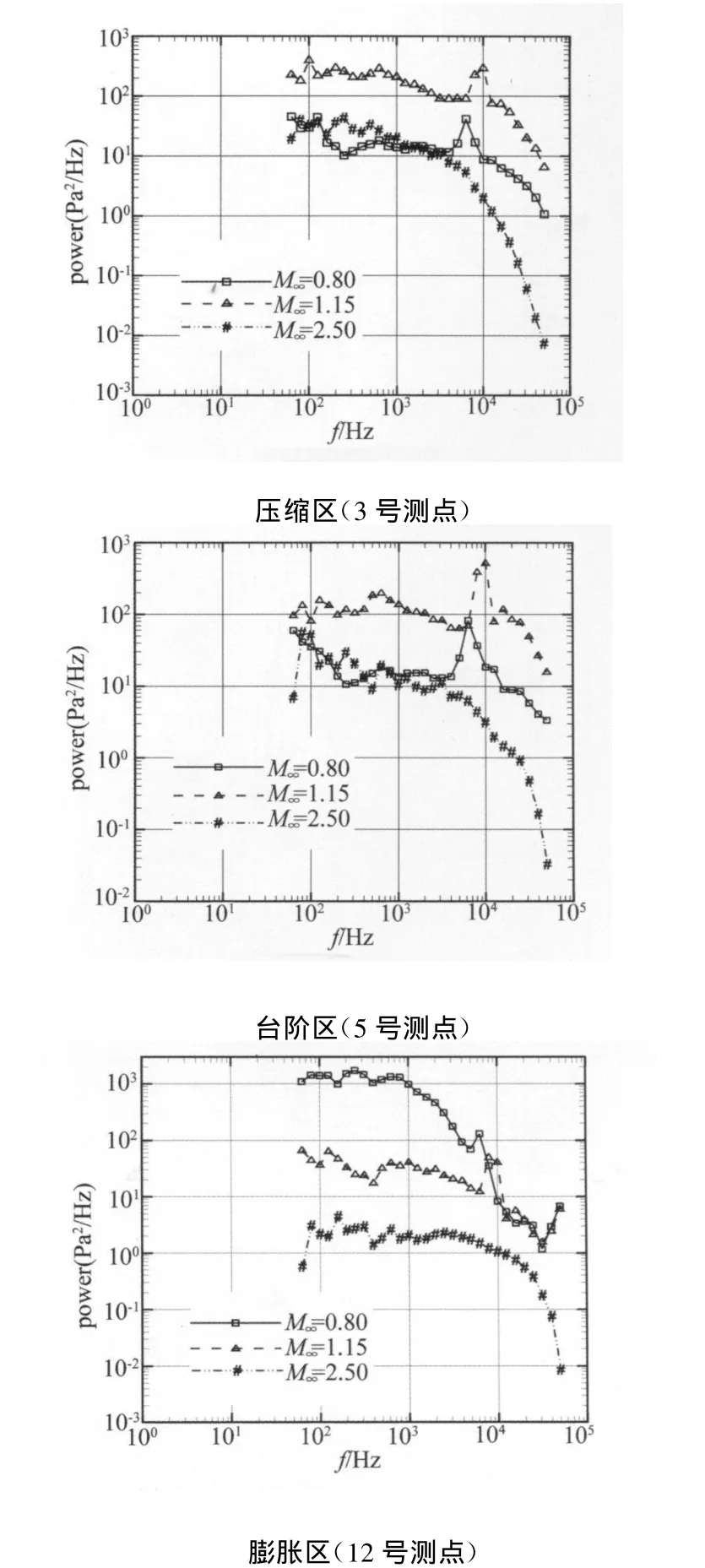
图6 功率谱曲线Fig.6 The curve of power spectrum density

2.3 脉动压力的空间相关性研究

研究非定常脉动压力环境的特征需要考虑该环境的空间相关函数,或者交叉互功率谱密度,它表示某点脉动压力的传播特性。按照相关系数的定义,相关系数是时间参数t的函数,此处考虑互功率谱密度函数Rxy的两个点在频域的积分,在t=0时刻相关系数最大,随着t的增大,相关性迅速衰减,在Rxy=±0.02范围内以脉动形式振荡,因此取了t=0时刻的相关系数加以分析。

图7 相关系数曲线Fig.7 The coefficient of correlation

图7给出了在迎角α=0°条件下,不同马赫数下弹体压缩区、台阶区及膨胀区的流向相关性曲线。可以看到,互功率谱密度曲线规律与湍流脉动相似。在弹体的压缩区,3号测点对上游的2号、1号测点几乎无影响,下游至4号测点即Δx/L=0.012区域内低度相关;在弹体的台阶区,5号测点对上游、下游区域的影响均为微弱相关;在弹体的膨胀区,12号测点对上游区域几乎无影响,至下游的 13号测点即 Δx/L=0.024的区域内为低度相关。流向相邻测点表现出一定的相关性,稍稍远离一点,相关性急速衰减至0.1,表明脉动压力具有强烈的局部特性。根据相关性理论可知,在弹体的膨胀拐角激波与膨胀波的相互作用区域内,测点间有相似的低频信号,应当有较大的相关性系数,而在相互作用区域之外,相关性有明显的减小。但是由于测点位置是根据模型尺寸按照相同间距进行布置的,从而不能直观的从相关性系数观察到激波振荡等区域的特点。

总体来看,相关系数结果普遍较小,表明测点间脉动压力的相关性较低。相关系数与马赫数变化基本无关,在迎角为α=0°条件下,各马赫数下沿轴向各个测点压力脉动之间的空间相关性有类似的分布规律。

2.4 脉动压力的重复性实验

图8分别给出了马赫数M∞=0.8、1.15,迎角为α=0°条件下,两次脉动压力实验的脉动压力系数对比曲线。可以看出,在相同来流条件下,两期实验的脉动压力系数规律基本一致,但有一定差别。

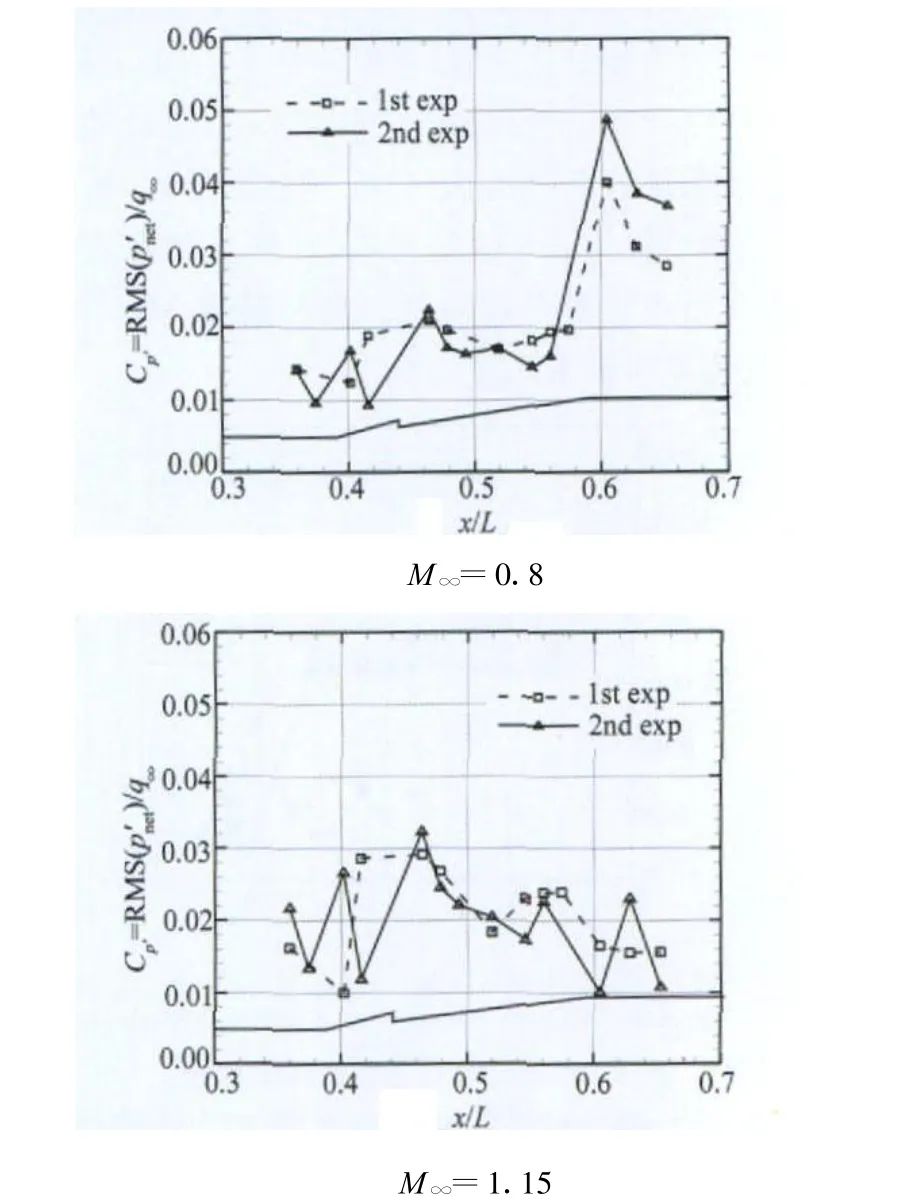
图8 两期实验的脉动压力系数对比曲线Fig.8 Contrast the coefficient of pressure fluctuation in two terms of experiments

图9给出了两次实验的脉动压力系数的相对误差。可以看出,对同一测点,两次实验的脉动压力测量值有一定差别,重复性实验有一定误差,尤其是在压缩拐角处差别较大。这可能是由于脉动压力本身的非定常性造成同一测点在不同次实验中脉动压力测量的幅值不同。

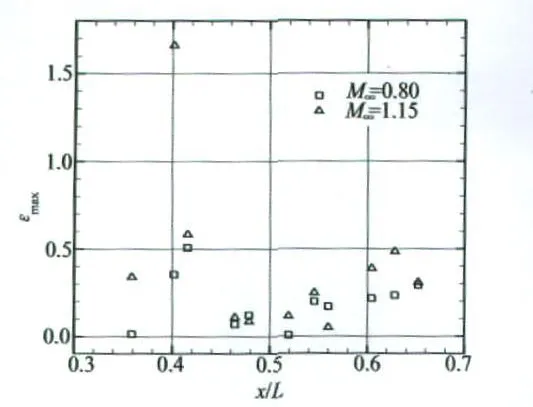
图9 两次实验脉动压力系数的重复性误差Fig.9 The repetitiveness error of pressure fluctuation coefficient in two terms of experiments

3 结 论

通过对弹体模型表面脉动压力的实验研究,可以得出如下结论：

(1)脉动压力系数总体上随着马赫数增加而降低;

(2)在实验迎角下,脉动压力系数在弹体表面曲率变化较小的位置基本上不随来流迎角的改变而变化;膨胀拐角肩部位置的脉动压力系数随着迎角的改变而变化较大;

(3)超声速来流条件下,脉动压力的功率谱能量峰值所对应的主频出现明显的低频特征;跨声速情况下,脉动压力的功率谱在6～9kHz处出现明显的峰值,且特征频率随着来流马赫数增大而增大;

(4)在来流迎角α=0°的条件下,实验中各测点沿轴向的脉动压力基本互不相关。且随着马赫数的变化,各个测点压力脉动之间的空间相关性有相似的分布规律。

致谢：

该工作得到了中国航天科技集团第十一研究院的刘子强研究员、赵磊高工的支持和帮助,作者在此表示诚挚的谢意。

[1]龙万花,陈伟芳,宋松和.旋成体跨声速脉动压力环境分析与预测[J].国防科技大学学报,2004,26(1)：17-20.

[2]COE C F,CHYU W J,DODS J B.Pressure fluctuations underlying attached and separated supersonic turblent boundary layers and shock waves[R].AIAA,73-996.

[3]DEGANI D,ZILLIAC G G.Experimental study of nonsteady asymmetric flow around an ogive-cylinder at incidence[J].AIAA Journal,1990,(28)：642-649.

[4]马宇,邓学蓥,刘沛清,等.细长旋成体大迎角扰流的背涡结构与压力脉动特性[J].空气动力学学报,2004,22(2)：165-170.

[5]李耀中.噪声控制技术[M].北京：化学工业出版社,2004.