基于微细梁振动位移的微尺度射流测速方法

周俊虎 ,汪 洋 ,杨卫娟,刘建忠 ,王智化 ,岑可法

(浙江大学能源洁净利用国家重点实验室,杭州 310027)

0 引 言

微尺度射流测速缺乏有效测量手段。常规测速方法主要有：皮托管、热线风速仪、激光多普勒测速(LDV)、粒子图像测速(PIV)等,均不适用于微尺度环境。皮托管干扰过大;热线风速计无法在变温流场中测速;LDV、PIV需要在气流中添加颗粒;涡街流量计受到雷诺数限制[1]。

微型喷射器的相关研究受到测量手段的制约。T.Geng[2]等研制的长 8cm,直径1.9cm微型喷射器,使用压电传感器测量其推力。Carole Rossi[3]设计的长1500μ m,直径108μ m 微型喷射器,由于无法测量,使用数值模拟得到运行参数[4]。

微型喷射器的设计与实验需要新的测速方法。因此本文提出利用微细梁在射流流场中的振动现象,测量微尺度射流流速。

微细梁作为MEMS(Micro Electro Mechanical Systems)机电结合的元件,具有响应快、精度高等优点[5]。其应用领域包括加速度[6-7]、磁力[8]、压力[9-10]、表面应力[11]、拉压力[12]、热量[13-14]、温度[15]、生物和化学力[16]、质量[17]等物理量的测量。也可以作为微型垂直驱动器使用[18]。

微细梁有动态和静态两种检测模式[19]。在动态检测模式下,被测量物理量的改变导致微细梁的谐振频率,弹性模量发生变化[20-21]。在静态检测模式下,梁的应力、尺寸等发生变化[15]。在动态检测模式下,微细梁需要通过静电、电磁、电热、激光等方式激振[22-23]。再以电容、电磁、压阻及激光等方式拾振[10]。而静态检测模式下,则可以使用干涉法等光学测量方法观察梁的形变[20]。

微细梁在振动时与周围气体产生流固耦合效应[24-25]。该试验研究在微尺度射流流场中,气流对微细梁冲击产生的振动,观察振动与气流速度间的关系。从而寻找可行的微尺度射流流速测量新方法。使用动态检测模式,并使用高速摄影和电磁方法记录梁的振动过程。

1 试验简介

试验系统如图1。气体通过微型喷管喷出,喷管直径约0.36mm。使用D07-12A/ZM型质量流量计测量管道中流量。将微细梁(实验中使用铜丝)垂直于来流方向放入流场中产生振动。梁的长度56.2mm、直径约0.07mm、质量0.009g。使用 Redlak Mothion Xtra HG-100K高速摄影仪拍摄微细梁的振动。拍摄帧频为250Hz。

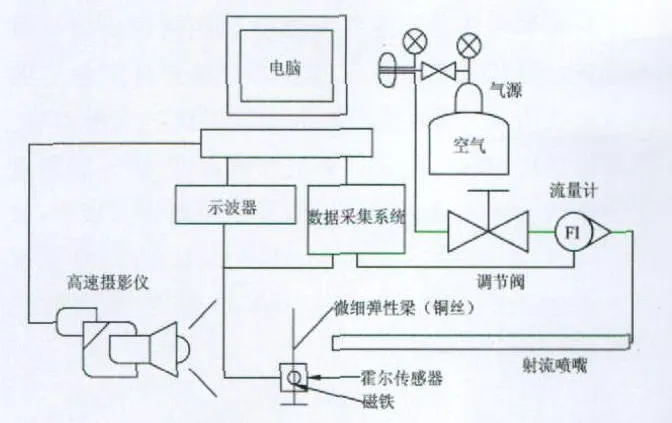
图1 实验装置系统图Fig.1 The schematic of experiment apparatus

使用霍尔传感器与磁铁测量梁的振动,如图2。磁铁固定在距梁的固定端36.8mm处,直径3mm、厚度2mm、质量0.0592g。霍尔传感器型号cs3503。振动过程中磁铁随梁偏移,当靠近传感器,输出高电压,反之输出低电压。振动时输出信号近似为交流电压,其有效值与振动幅度相关。使用hp34970a型数据采集仪和示波器分别测量输出电压有效值和完整信号。

实验观察了射流喷嘴对准梁的三处不同位置的振动情况,以比较射流气体在梁上的作用点位置对振动的影响。作用点均位于梁的前半段,以增加射流气体的力臂,使振动更明显。实验过程为：根据表1设置喷管位置,喷口与梁横向距离约14.8mm,如图2(b)所示。打开气路产生射流引发振动。振动稳定后将管内流量调至100mL/min,每隔约100s提升200mL/min,直至1000mL/min。改变喷嘴位置,重复实验。分别使用高速摄影仪和霍尔传感器对相同的工况进行测量,使用高速摄影仪时不安装磁铁。

图2 霍尔传感器测量微细梁的振动Fig.2 The schematic(a)and picture(b)of measurement with magnet

表1 各位置喷嘴距离梁位置Table 1 The distance between nozzle and copper thread in different cases

2 实验结果

根据射流公式(1)[26]将管内流量100～1000mL/min换算为流速2.7～27.3m/s。

x0为速核长度;vx为轴心上距喷口x处速度;v0为喷口出口处的速度;d0为喷嘴宽度;a为湍流系数。

位置2、流速27.3m/s时梁的1周期振动过程如图3。按照经典圆柱绕流理论,绕流过程中,流体发生边界层脱离,导致压差阻力的形成;流体自身的粘性产生粘性阻力。两种力共同构成气流对梁的作用力。将微细梁垂直于来流方向放入流场中。初始时,气体对微细梁的作用力垂直于梁,并使梁顺应流动方向弯曲。随着梁的弯曲倾斜,梁正对来流的迎风面积减小,气流作用力降低。当梁自身弹性回复力超过气流作用力时,梁开始向反方向摆动,形成强迫振动过程。

定义梁自由端顶端与参考中线的距离为梁的最大偏移。高速摄影仪拍摄的喷嘴处于不同位置时,梁的最大偏移随射流速度变化曲线如图4、5。位置1在最低流速5.46m/s时,偏移高于相同流速下其他位置的偏移。因为此时喷嘴对准梁9/10处,气流作用力矩较大。随后偏移随射流速度增加,直至16.3m/s时,最大偏移在左右侧分别达到 10.2和5.07mm。此后偏移小幅下降。喷嘴对准梁3/4处(位置2),流速5.46m/s时偏移比位置1时低。流速达到21.8m/s,梁在左右侧的偏移分别达到11.1和8.57mm。此后梁偏移随流速增长变缓。射流喷嘴对准梁3/5处(位置3),流速5.46m/s时偏移约2.28和-0.840mm,低于前两位置。但随流速上升直至27.3m/s,偏移保持增加。

喷嘴处于位置1和2,射流速度较高时,偏移不再上升,这可能由于流速不均。近喷口处流速较高,抑制梁的逆流动方向偏移。但是在位置3,梁偏移时远离射流喷口,不受近喷口强气流的抑制,因此偏移始终随流速上升。位置1和2在低射流速度下偏移更高,因此灵敏度更高。

图3 位置2气流速度为27.3m/s时梁振动1周期的过程(中间直线为参考中线)Fig.3 The vibration of cantilever during one period atposition 2 with flow rate of 27.3m/s(the line in the middle is the reference)

图4 不同位置时的流速与梁向左侧的最大偏移Fig.4 The maximum left displacement of the cantilever vs flow rate at different flow rates

图5 不同位置时的流速与梁向右侧的最大偏移Fig.5 The maximum right displacement of the cantilever vs flow rate at different flowrates

较大的偏移始终位于参考中线左侧。如位置1左右偏移差最大达到5.8mm。这是由于梁逆流动方向运动时,与流体作用力方向相反,运动受抑制。反之运动增强。

三个位置处,梁的振动频率均为约22Hz,可能工作在共振频率处。与悬臂梁共振频率公式(2)计算得到理论共振频率10.8Hz相比,相差约10Hz。偏差可能由于梁周围气流的粘性所致。

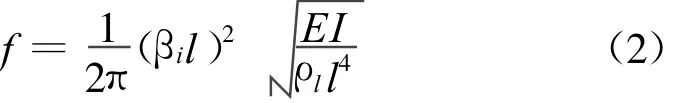
f-共振频率;βi-常数;E-梁的杨氏模量;ρl-梁线密度;I-梁截面弯曲惯性矩;l-梁长度。

对霍尔传感器与磁铁所测量到的梁振动情况进行分析。位置2霍尔传感器和质量流量计的输出曲线对比如图6。两曲线均显示出阶梯状的递增趋势。质量流量计的输出稳定性和线性度很好,但只能测量管内流量。霍尔传感器输出信号在两端波动较大,如t＞700s时波动最大为0.0179～0.0199V。流量由800mL/min上升到1000mL/min过程中,响应时间较慢,约16s,如小图所示。

图6 位置2霍尔传感器输出电压有效值与质量流量计随时间变化曲线(小图中为630～650s时间段放大曲线)Fig.6 The effective voltage output of the Hall sensor and flow rate vs time at postion 2(the mini figure gives the magnified plot during the time of 630～650s)

示波器采集的位置2处的霍尔传感器输出信号如图7。比较不同射流速度下的霍尔传感器信号,发现振动频率保持在10Hz,低于之前观察到的22Hz。由于梁上装有磁铁,使振动频率下降。

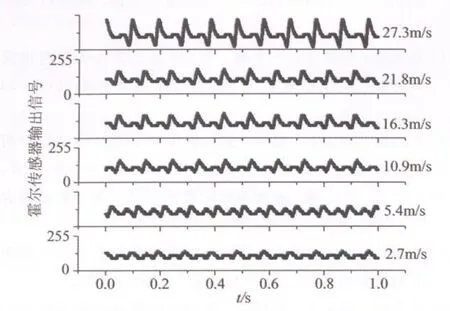
图7 位置2时示波器采集的霍尔传感器输出信号(1s内)Fig.7 The signal output of Hall sensor at position 2 measured by oscillograph(within 1s)

图8汇总各位置霍尔传感器的输出有效电压随射流流速变化曲线。位置1时,在流速2.7～10.9m/s时,输出信号随流速增长。当流速超过16.3m/s,梁的振型发生变化,振动完全转移到梁前半段,而梁中间的磁体不动,因此输出信号为0。这是由于磁铁改变了梁的质量分布造成的。在位置2时,喷嘴对准梁的3/4处,结果显示较好的单调线性,线性拟合结果为公式(3),截距与斜率的标准误差分别为6.34×10-4、3.87×10-5。实际使用中须通过标定得到霍尔传感器的有效电压与流速的关系式后,通过测量实际电压得到射流速度。位置3时,喷嘴对准梁的3/5处,磁铁位于射流流场中,带来很大干扰,因此信号输出无规律。当流速大于10m/s时开始振动,但输出信号与流速成反比。

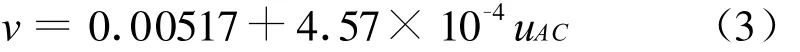
图8 梁振动时的射流流速-霍尔传感器输出有效电压曲线Fig.8 The effective voltage outputof Hall sensor vs flow velocity during cantilever vibration

3 结 论

对微细梁在微尺度射流流场中振动进行实验,使用高速摄影仪观察了喷嘴对准梁的三处不同位置时,射流流速2.7～27.3m/s振动现象。当射流喷嘴对准梁的3/5处时,振幅随流速线性变化,由约0mm上升到10mm。但在其他两处位置时,在低流速度段2.7～10.9m/s时,振幅保持随流速上升。但当流速超过16.3m/s,振幅上升缓慢,甚至小幅下降。

提出将该现象用于微尺度射流测速。使用磁铁与霍尔传感器测量振动。当喷嘴对准梁3/4处时,输出信号随流速线性上升。输出电压有效值与流速拟合公式为：v=0.00517+4.57×10-4uAC。但当喷嘴对准梁的另两处位置时,由于安装磁铁改变了梁的质量分布和梁周围的流场,使振动随流速变化不规律。因此将微细梁振动用于微尺度射流测速,有必要针对振动稳定性作进一步改进。

[1]黄咏梅,张宏建,孙志强.涡街流量计的研究[J].传感技术学报,2006(3)：776-782.

[2]GENG T,ZHENG F,KIKER A P,et al.Experimental and numerical investigation of an 8-cm valveless pulsejet[J].Experimental Thermal and Fluid Science,In Press,Corrected Proof.

[3]ROSSI C,ESTEVE D,MINGUES C.Pyrotechnic actuator：a new generation of si integrated actuator[J].Sensors and Actuators A：Physical,1999,74(1-3)：211-215.

[4]ORIEUX S,ROSSI C,ESTEVE D.Compact model based on a lumped parameter approach for the prediction of solid propellant micro-rocket performance[J].Sensors and Actuators A：Physical,2002,101(3)：383-391.

[5]田文超,贾建援.Mems微梁粘附“突陷”静力分析[J].机械科学与技术(西安),2005,24(1)：48-50.

[6]范波,熊继军,郭涛,等.八梁硅微加速度传感器横向灵敏度的研究[J].传感器与仪器仪表,2008,24(1-1)：138-140.

[7]裘安萍,岩苏,芹施,等.硅微振梁式加速度传感器中微杠杆结构的设计[J].传感技术学报,2006,19(15)：2204-2207.

[8]FINOT E,THUNDAT T,LESNIEWSKA E.Measuring magnetic susceptibilities of nanogram quantities of materials using microcantilevers[J].Ultramicroscopy,2001,86(1/2)：175-180.

[9]樊尚春,李明明,宋治生.硅谐振梁式压力微传感器边界结构参数优化[J].航空学报,1999,20(4)：362-364.

[10]陈德勇,崔大付 ,等.微结构谐振梁式压力传感器研究[J].传感技术学报,2000,(4)：255-259.

[11]李凯,张青川,刘红,等.微梁传感研究pnipam分子链热致折叠构象转变[J].实验力学,2006,21(3)：259-264.

[12]杨俊英,李孟源,郭爱芳.微型s梁拉压力传感器的研制[J].洛阳工学院学报,1998,19(1)：33-37.

[13]BARNES J R,STEPHENSON R J,WOODBURN C N.A femtojoule calorimeter using micromechanical sensors[J].Review of Scientific Instruments,1994,65(12)：3793-3798.

[14]BARNES J R,STEPHENSON R J,WELLAND M E.Photothermal spectroscopy with femtojoule sensitivity using a micromechanical device[J].Nature 1994,372(3)：79-81.

[15]李艳宁,赵景,郭彤,等.温度变化对微梁谐振频率的影响[J].天津大学学报,2008,41(1)：7-10.

[16]FLORIN E,MOY V T,GAUB H E.Adhesion forces between individual ligand-receptor pairs[J].Science of The Total Environment,1994,264(5157)：415-420.

[17]VILLARROYA M,VERD J,TEVA J.Systemon chip mass sensor based on polysilicon cantilevers arrays for multiple detection[J].Sensors and Actuators A：Physical,2006,132(1)：154-164.

[18]方华军,刘理天.压电折叠梁微执行器的低电压优化设计[J].传感技术学报,2008,21(3)：465-468.

[19]李艳宁,赵倩云,王忠顺.用压电探针提高轻敲模式afm在液体中的成像性能[J].西安交通大学学报,2006,40(3)：341-343.

[20]张天林,郭哲颖,张青川,等.微梁传感器弹性模量的测试[J].中国科学技术大学学报,2006,36(5)：567-572.

[21]蒋庄德,卢德江,王小斌,等.微型梁杨氏模量与内应力的固有频率法测量[J].西安交通大学学报,2000,34(5)：55-58.

[22]兰之康,唐洁影.Mems微梁疲劳频率特性测试与分析[J].功能材料与器件学报,2008,14(1)：89-92.

[23]李雪莹,周浩敏.硅谐振梁式微传感器同频干扰的研究[J].测控技术,2004,23(2)：17-18.

[24]李普,胡如夫,尹垚.弹性悬臂微梁谐振系统挤压膜阻尼新解析模型[J].振动与冲击,2008,27(3)：21-26.

[25]杜全根,胡元太,陈传尧.微梁谐振器高阶振动时的挤压薄膜阻尼效应[J].华中科技大学学报,2003,31(10)：79-81.

[26]黎惠霖,阮伯如.射流技术及其应用[M].北京：机械工业出版社,1977.