水中结构振动特性的实验研究*
2010-04-10杨吉新秦延飞刘素云陈海平
杨吉新 秦延飞 刘素云 陈海平
(武汉理工大学交通学院1) 武汉 430063) (广东省冶金建筑设计研究院2) 广州 510300)
内陆江河水库工程中有一些水中结构如大坝、桥墩等,这些水中结构受到动荷载作用时将会产生振动.这种振动通过对界面的激励,在水中产生附加的动水压力,而附加的动水压力又通过界面引起结构的动力响应.此类水-结构的耦合振动作用是一个比较复杂的过程,相应的研究还有待深入.过去由于水深不大,设计时采用了过度简化的计算方法.随着海洋工程的不断发展,水中结构的数量不断增加的同时,水深也越来越大,如正在规划中的跨海桥梁,水深将在百m以上,某些海洋平台所涉及的水深甚至达数百m,水对结构物的动力影响将非常大.这些水下结构的设计不仅要考虑结构物在空气中的振动问题,而且要考虑结构物与流体耦联时的振动问题,保证结构设计合理,使用可靠[1-2].为了分析水介质对结构振动的影响,本文进行了水中结构振动特性实验研究.
1 实验模型及实验装置
1.1 模型设计
根据目前实际工程中悬臂梁柱受激励时的振动情况,通过模型实验找出不同水深对不同截面的悬臂梁的影响程度.因此,结合结构工作环境及安装条件,并考虑实际工程要求,本实验制作了3组悬臂梁模型,见图1.模型试件固接在200 mm×200 mm×10 mm的底板上,模型材料采用钢材,其密度为785 0 kg/m3,弹性模量为210 GPa,泊松比为0.3,模型尺寸见表1所列.
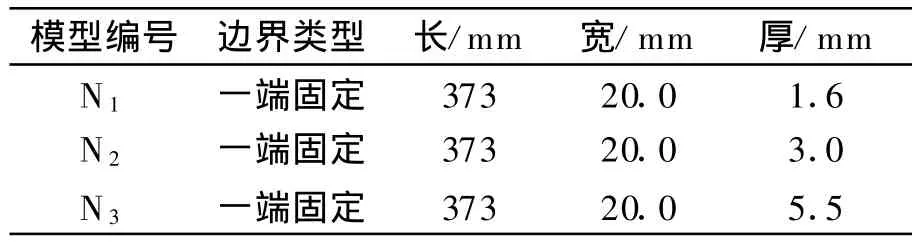
表1 模型尺寸
1.2 实验装置
实验装置包括水槽和量测系统.
水槽.长 70 cm,宽 60 cm,高 60 cm,见图 2.

图1 试件

图2 水槽
量测系统.振动量测采用INV1601B型振动实验仪、INV306U系列智能信号采集处理分析仪、INV型激振锤、INV型非接触式激振器、电涡流位移传感器、DASP数据采集与信号处理软件,见图3~4所示.

图3 实验台

图4 传感器和激振器布置图
2 空气中的模型试验
在进行水中试验前分别采用有限元软件ANSYS和VSES对3组试件的振动频率进行分析.两种软件的计算结果基本相同,见表2.
在计算的基础上,分别用共振法和模态法对3组悬臂梁柱进行了空气中的模型试验.
2.1 实验方法与步骤
1)共振法的实验步骤

表2 试件的计算频率
步骤1 将仪器安装连接,放置好非接触式电涡流传感器和激振器,使传感器和激振器离试件3~5 mm,为了防止底座受激振时和悬臂梁一起振动,在底座上放置一些铁质重物加强底座的稳定性[3-4].
步骤2 通过人工激励识别悬臂梁柱的估计基频值.
步骤3 调节INV型非接触式激振器的频率,使其频率在估计基频值附近变动,悬臂梁柱受到激励发生振动,这时电涡流传感器识别出信号,通过振动试验仪和分析仪输入计算机,在DASP软件中显示出频率和最大振幅.
步骤4 缓慢调节激振器,同时观察悬臂梁柱的振幅,当振幅最大时可以判断悬臂梁柱达到共振,此时的频率就是悬臂梁柱的1阶频率f1.
步骤5 悬臂梁柱的2、3阶频率可在6.25f1,17.5f1附近调节,观察悬臂梁柱的振型、频率和最大振幅,可得到悬臂梁柱的2,3阶频率.
2)模态法的实验步骤
步骤1 将仪器安装连接,为了防止底座受激振时和悬臂梁一起振动,在底座上放置一些铁质重物加强底座的稳定性[5].
步骤2 将试件沿梁长方向划分9等份即在试件上标定10个节点,将电涡流位移传感器放置在第4个节点处.
步骤3 打开DASP软件进入模态实验界面,设置模态实验测试参数.触发采样时用激振锤分别敲击各节点3次,然后进行传函分析得到幅频曲线,得到试件的各阶频率,输出模态分析报告.
2.2 实验结果
通过共振法和模态法2种方法分别测试了3组试件的基频,实验结果见表3.
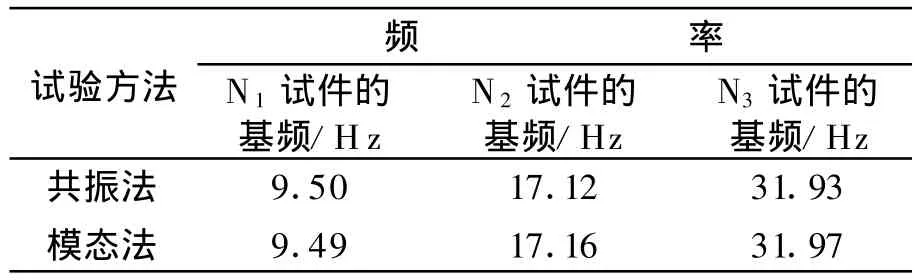
表3 空气中模型试件的基频
2.3 实验分析
2种方法测试的结果基本相同,最大误差只有0.23%,对比表2和表3可以看出实验结果与计算结果基本吻合,说明实验方法的可信性.
3 水中模型试验
3.1 实验步骤
悬臂梁柱在水中的自振频率的量测步骤如下.
步骤1 将仪器安装连接,试件固定在水槽中央,水位达到试件115 mm高处,为了避免水的浮力影响模型的振动和底座受激振时和悬臂梁一起振动,在底座上放置一些铁质重物加强底座的稳定性.
步骤2 用硅胶密封好传感器和激振器并放置在水槽中,使传感器和激振器离试件 3~7 mm..
步骤3 调节INV型非接触式激振器改变激振的频率,使其在空气中测得的基频值附近变动,悬臂梁柱受到激励发生振动,这时传感器识别出悬臂梁柱的频率和最大振幅,结果通过振动试验仪和分析仪输入计算机,在DASP软件中显示出频率和最大振幅.
步骤4 缓慢调节激振器,同时观察悬臂梁柱的振幅,当振幅最大时可以判断悬臂梁柱达到共振,此时的频率就是悬臂梁柱在水深115 mm处的 1 阶频率.
步骤6 用同样的方法可得到在水深265 mm、满水(373 mm)情况下悬臂梁柱的1,2,3阶自振频率.
3.2 实验结果
不同水位下悬臂梁的一阶频率与无水频率相比的变化情况如图5~7所示.
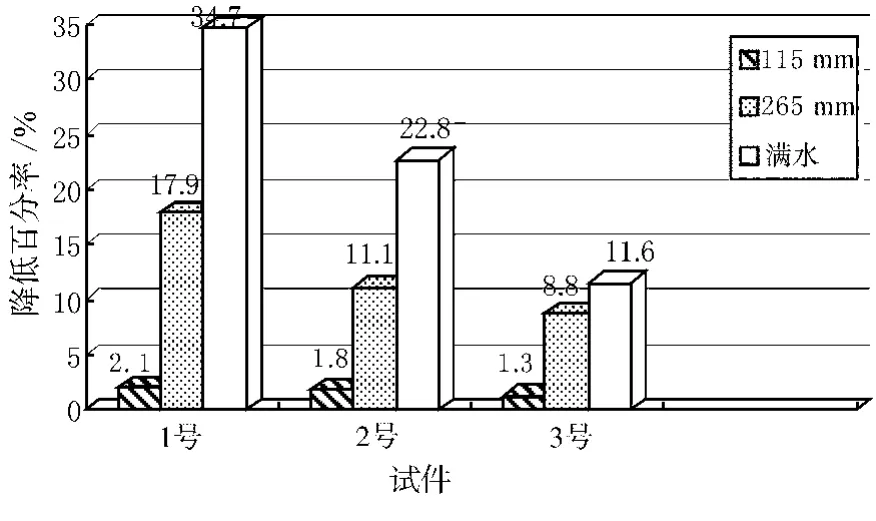
图5 不同水位下悬臂梁柱一阶频率与无水频率相比降低的百分率
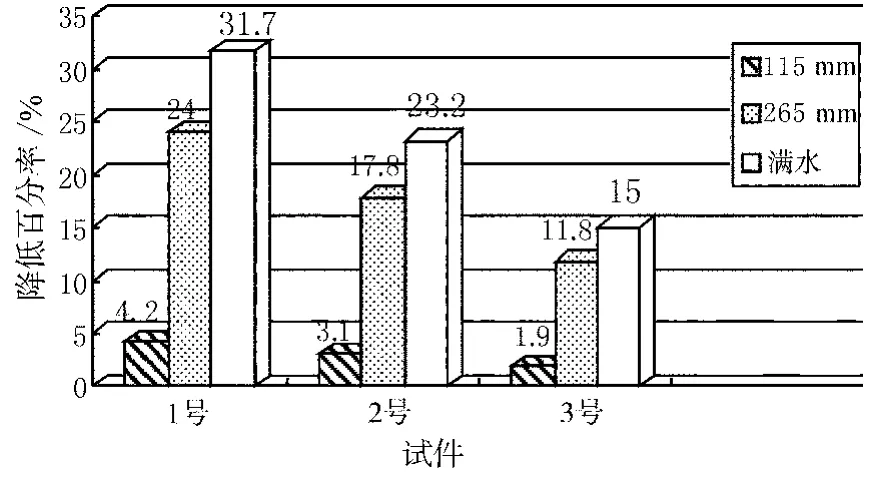
图6 不同水位下悬臂梁柱二阶频率与无水频率相比降低的百分率
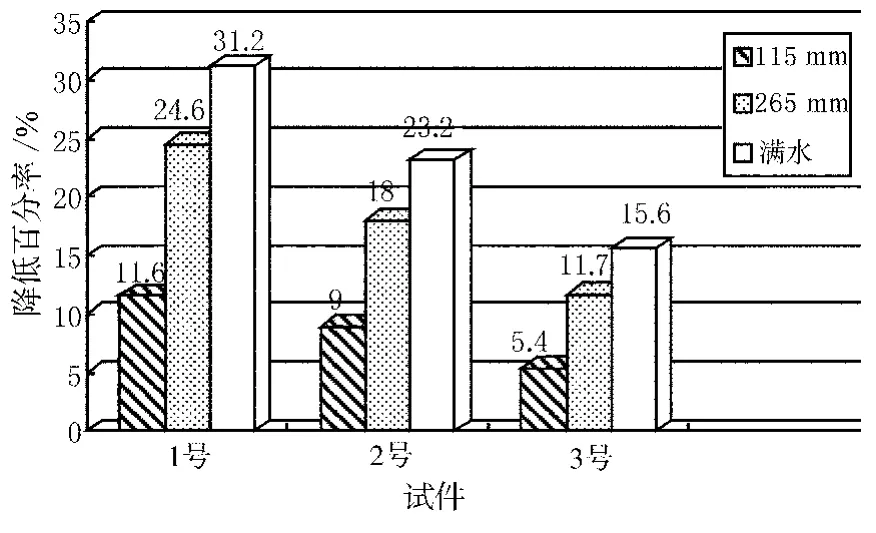
图7 不同水位下悬臂梁柱三阶频率与无水频率相比降低的百分率
3.3 实验数据分析
通过图5~7可以得出如下结论.
1)利用数值计算和2种实验不同方法获得了悬臂结构在空气中的基频,计算数据和实验结果基本吻合,说明共振法测试结果的可信性.
2)通过水-悬臂梁的耦合振动实验,证明了附联水质量会降低结构的自振频率,结构在水中的固有频率均比空气中低.
3)随着水深的增加,悬臂梁柱各阶固有频率降低程度逐渐加大,当水位到达悬臂梁柱高度265 mm(71%)时,水对结构的自振频率的影响已很大(1号试件最高达24.6%),因此,工程设计计算时应予以考虑.
4)随着水深的增加,三阶频率降低的百分率最高,一阶频率相对低些,说明悬臂梁柱的基频受水深影响比高频小.但满水时各阶频率降低的百分率相差不多,这可能由于悬臂梁最高点是各阶模态振动位移最大处,所以满水对各阶频率的影响都很大.刚度较小的1号悬臂梁柱的一阶频率降低的百分率比其他两阶稍大.
5)3组试件水中各频率与无水频率相比降低的百分率可以看出随着水深的增加,1号悬臂梁降低的百分率最大,3号悬臂梁最小,说明刚度较小结构的固有频率受水阻尼影响较大,所以,设计深水域中如桥墩细长结构时一定要考虑水动力作用的影响.
4 结束语
水-结构的耦合振动是一个比较复杂的问题,鉴于工程需要和研究的不足,本文进行了水中结构振动特性实验研究,讨论了水深对振动特性的影响,得出了一些可供工程设计参考的数据和结论.但限于条件,本文只以较简单的模型进行了振动特性实验,对于更复杂的问题如复杂形状、复杂边界条件下的水中结构振动特性及其动力响应等还有待进一步研究.
[1]居荣初,曾心传.弹性结构与液体的耦联振动理论[M].北京:地震出版社,1983.
[2]丁思远.粘性流体对结构固有频率及阻尼的影响[J].郑州轻工业学院学报,1994,9(4):50-53.
[3]林圣华.结构试验[M].南京:南京工学院出版社,1987.
[4]张 敏.桥墩与河水流固耦合振动分析[D].大连交通大学土木与安全工程学院,2006.
[5]左东启.模型实验的理论和方法[M].北京:水利电利出版社,1984.
