(G′/G)展开法的简化及Nagumo方程的有界行波解

李向正 ,张卫国 ,原三领

(1.上海理工大学理学院,上海 200093;2.河南科技大学数学与统计学院,河南洛阳 471003)

0 前言

王明亮、李向正和张金良于 2008年提出了(G′/G)展开法[1],尔后受到了国内外同行的大量关注,在国际重要期刊上已有几十篇论文提到或应用该方法[2-5]。(G′/G)展开法的主要思想是借助(G′/G)变换,利用众所周知的二阶线性常系数常微分方程及其一般解,来求出非线性发展方程的行波解。(G′/G)展开法揭示出了非线性方程的解可以用线性方程的解来构造,从而充分利用了线性常微分方程理论。文献[2]将(G′/G)展开法推广到了变系数非线性演化方程。文献[3]将(G′/G)展开法应用到了高阶非线性发展方程。文献[4]将(G′/G)展开法应用到了时滞非线性演化方程。文献[5]将(G′/G)展开法应用到了高维非线性物理方程。

本文拟对(G′/G)展开法做进一步简化。在文献[1]的(G′/G)展开法中,所用的二阶线性方程是

其中λ,μ为待定常数。由常微分方程定性理论研究表明,方程(1)可以简化为:

其中δ∈{-1,0,1},这样并不失一般性。由于方程(2)与方程(1)相比,减少了参数且限定了 δ的取值,方程(2)解的表示式十分简洁。用更少的参数就可得到同样本质的结果。下面将简化后的(G′/G)展开法应用于Nagumo方程,求出其各种有界的行波解,并分析它们的性态。

1 Nagumo方程及其有界行波解

大脑是人体最为复杂的信息处理系统。联想记忆是人脑的重要认知功能之一。由于许多神经活动很难在实验室中直接被观察,需要通过建立神经网络模型对脑的联想记忆功能进行仿真。20世纪 90年代,研究表明发放神经元表现出了联想记忆的特性,更加接近真实生物神经元。因此,由发放神经元模型构成的联想记忆神经网络模型成为目前国际科学研究的热点,其中Hodgkin-Huxley模型(简称HH模型)、FitzHugh-Nagumo模型(简称FHN模型)就是典型的发放神经元模型[6]。

HH模型是Hodgkin和Huxley于1952年通过对神经纤维中神经冲动传播的研究而提出的,它是用来描述神经元的轴突中膜电位与膜电流之间关系的一组微分方程组[7]。该方程组是可兴奋细胞的经典模型。FHN模型是对HH模型的简化[8]。描述神经元的模型要显示的基本特征是:一个脉冲或者迅速地衰减(阈下的),或者形成典型形式沿着神经元的轴突传导下去,像行波一样。由于非线性 HH模型和FHN模型的复杂性,长期以来缺乏一种求出其解析解的方法,因而常借助数值方法进行研究[7-10]。

FitzHugh-Nagumo方程(简称FHN方程)[6]:

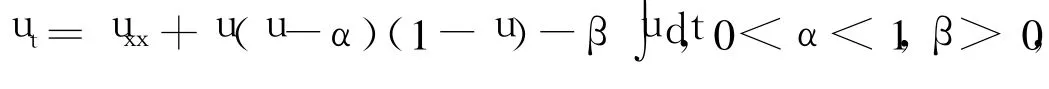
是对HH模型的合理模仿,并且基本特征不会失去。FHN方程用来模拟遗传特性的散布、神经脉冲在神经轴突上的传播等。参数 α是与细胞膜性质相关的参数,是由细胞膜的电特性决定的。FHN方程中参数β=0时,即得到Nagumo方程[9]:

Mckean[9]介绍了Nagumo方程的研究进展。Iqbal[10]研究了求Nagumo方程数值解时参数的取法。然而仍有一些问题需要研究,如Nagumo方程有无其他形式的精确解,得到的解之间有什么关系。本文将简化后的(G′/G)展开法应用于Nagumo方程,获得其更多的有界行波解,并对解之间的关系进行简单分析。

要寻找Nagumo方程(3)的行波解:

其中,K＞0为波数;ω为角频率;ξ0为常数。将式(4)代入方程(3)得q满足的常微分方程:

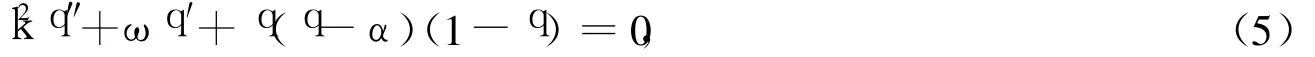
方程(5)属于Lienard方程。

根据齐次平衡原则[1,11],可设方程(5)有如下形式的解:

其中,G=G(ξ)满足方程(2);a0,a1为待定常数。将式(6)代入方程(5)中,利用方程(2)可将方程(5)左端转化为关于(G′/G)的多项式,令(G′/G)的各幂次项的系数为0,得到关于a0,a1,k,ω和δ的代数方程组(方程组右边n代表(G′/G)的幂次):

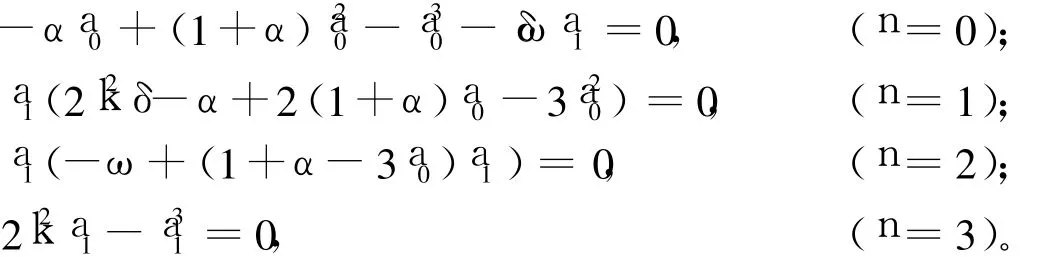
解上述方程组得9组解:

将式(7)～式(15)9组解分别代入式(6),利用方程(2)的解,可得到Nagumo方程(3)的行波解:

其中,ξ=(2/4)x-((1-2α)/4)t+ξ0,称为相变量;A1,A2为任意常数。若取A2=0,即得:

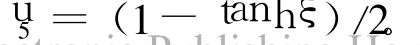
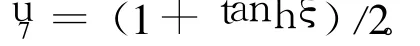
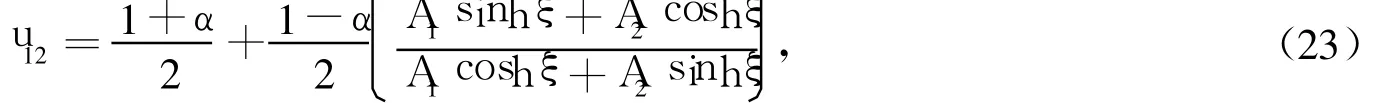
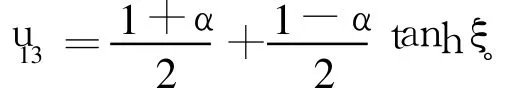
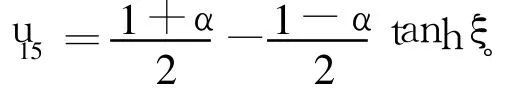
2 结论

利用简化后的(G′/G)展开法求解Nagumo方程,获得了9个解。

(1)其中平凡解u1=0,u2=α和u3=1界定了其余 6个非平凡有界行波解的运动范围。

(2)二阶线性方程的参数减少且仅取δ∈{-1,0}3个特殊值,使得方程的解的表达式简洁了,(G′/ G)的表达式也简洁了,且这些简化并不破坏解的本质特征。

(3)二阶线性方程及其相应解的简化使得计算过程变得简洁了,如减少了代数方程组中的参数,解的整理也减少了步骤。

致谢:感谢王明亮教授的帮助和指导。

[1] Wang M L,Li X Z,Zhang J L.The(G′/G)-expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics[J].Physics Letters A,2008,372:417-423.

[2] Zhang J,Wei X L,Lu Y J.A generalized(G′/G)-expansion Method and Its Applications[J].Physics Letters A,2008,372: 3653-3658.

[3] Gao H,Zhao R X.New Application of the(G′/G)-expansion Method to Higher-order Nonlinear Equations[J].Applied Mathematics and Computation,2009,215:2781-2786.

[4] Hyunsoo K,Rathinasam y S.Travelling Wave Solutions for Time-delayed Nonlinear Evolution Equations[J].Applied Mathematics Letters,2010,23:527-523.

[5] 马玉兰,李帮庆,孙践知.(G′/G)展开法在高维非线性物理方程中的新应用[J].物理学报,2009,58:7402-7409.

[6] 张伟,乔清理.联想记忆人工神经网络的发展和研究现状[J].医疗卫生装备,2008,29(5):36-38.

[7] Hodgkin A L,Huxley A F.A Quantitative Descrip tion of Membrane Current and Its Application to Conduction and Excitation in Nerve[J].Journal of Physiology,1952,117:500-544.

[8] Fitzhugh R.Impulses and Physiological States in TheoreticalModels of Nerve Membrane[J].Biophysical J,1961,1:445-466.

[9] Mckean H P.Nagumo's Equation[J].Advances in Mathematics,1970(4):209-223.

[10] Iqbal M.Numerical Solutions of Nagumo's Equation[J].Journal of Applied Mathematics＆Decision Sciences,1999,3 (2):189-193.

[11] 李向正,张小勇,赵丽英.修正Euler-Painlevè方程的线性化解法[J].河南科技大学学报:自然科学版,2007,28 (2):70-71.