二维翼型抽吸气层流控制技术的数值研究

段会申,刘沛清,陈建中,2,佟增军

(1.北京航空航天大学航空科学与工程学院,北京 100191;2.中国空气动力研究与发展中心,四川 绵阳 621000)

0 引 言

高效减阻是飞机设计师和制造者的一个长期目标,通过减小飞行阻力可降低飞机运行成本,同时还能减少燃料污染物的排放,从而降低空中环境污染,这在科学技术高速发展的当今时代显得尤为重要[1]。在已经探索的众多控制技术中,层流控制技术(LFC)在减阻方面拥有较好的潜能,该技术通过稳定边界层,延迟边界层转捩,扩大物面的层流流动区域,从而达到减小摩擦阻力。目前,混合层流流动控制技术(HLFC)是大型运输机最有效的减阻技术之一[2-4]。该技术是机翼前缘表面修形(保持较好的顺压梯度)和离散孔表面抽吸气技术的结合。其中,表面抽吸气稳定边界层包含两种机制,其一是改变边界层平均速度分布来获得更稳定、更饱满的速度剖面;其二是减小边界层位移厚度雷诺数[5]。已有的研究表明[6],最稳定的层流边界层可以通过连续多孔表面的理想吸气获得。然而,理想吸气只是一个概念,理想表面并不存在。当前的抽吸气控制均采用离散孔表面的不连续局部吸气来实现。

尽管通过离散孔的不连续表面吸气可以稳定边界层和推迟转捩的发生,但这项技术对外部环境因素的干扰,以及孔的形状、孔径、孔间距、孔隙率、吸气流量和位置等吸气参数的影响十分敏感。这是由于边界层内部的不稳定波对表面吸气十分敏感,吸气参数的微弱改变都会对边界层的稳定性有较大的影响[5-6]。因此,在进行层流流动控制系统和多孔表面设计之前,开展相关吸气参数的研究是非常必要的。目前,从现有的公开发表的吸气层流控制综述文献[2]来看,大多数是关于固定孔径和孔间距的多孔表面吸气对飞机机翼阻力影响的飞行试验和风洞实验研究,而关于不同吸气参数对边界层稳定性、转捩位置和阻力等影响的研究甚少。

基于上述原因,在前人研究成果的基础上,本文进行了孔径、孔间距、和吸气区位置等吸气参数的数值模拟,主要研究了吸气参数对二维翼型转捩位置、摩擦阻力、压差阻力以及总阻力的影响,通过对数值模拟结果的比较分析,给出了相应的变化规律。

1 数值计算方法

1.1 湍流转捩模式修正

本文数值计算的湍流模型采用剪切应力输运(Shear Stress Transport,SST)两方程模型,边界层转捩模拟选用Wilcox低雷诺数转捩模式。由于SST k-ω湍流模式中的Wilcox低雷诺数转捩预报模式对扰动过于敏感,使得计算的转捩位置比实际情况明显靠前,因此有必要对其进行修正,从而提高预报精度。SST k-ω湍流输运方程如下:

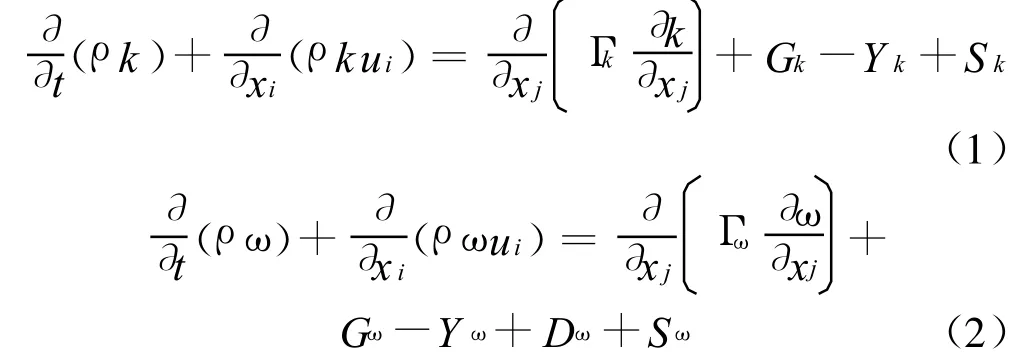
其中:Gk和Gω为方程的生成项,Yk和Yω为方程的耗散项,Γk和Γω为扩散系数,且有:

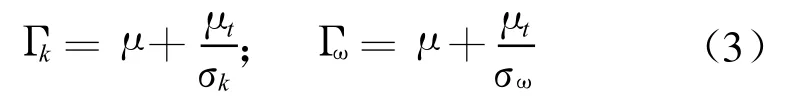
式中 μ为层流粘性系数,μt为湍流粘性系数。就SST k-ω湍流模型而言,湍流粘性系数的表达式为:

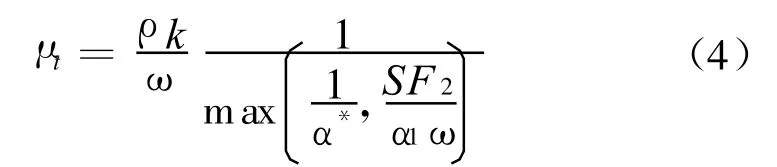
式中:S是剪切应变率的模;α1为常数;F2为混合函数,用于改进湍流粘性系数在壁面逆压流动区域的结果。在高雷诺数下,间歇函数α*=1,此时流动为湍流。如果考虑低雷诺数流动(转捩)的影响,Wilcox的间歇函数表达式如下:

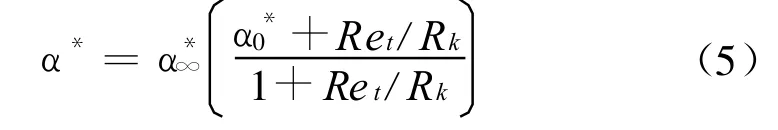
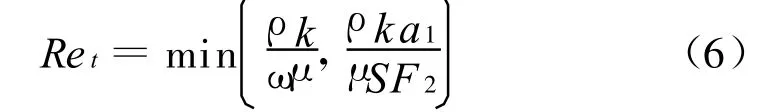
1.2 物理模型及求解方法

本文数值计算选用RAE2822翼型,这是一个典型的跨音速翼型。如图1所示,翼型沿弦向0～30%弦长区域为吸气控制区。此次计算翼型上翼面自然转捩点位置均在30%弦长范围内,又因吸气控制区一般应在自然转捩点上游,因此将吸气区等分为6个区域(图1)。翼型周围的网格见图2,网格划分使用Gambit软件,为了更好地模拟边界层流动,壁面第一层网格满足y+=0.2～1。由于吸气孔径相对于翼型弦长很小,因而在保证计算精度的前提下,为了尽可能减少网格数量节省计算量,对孔周围网格进行局部加密,计算域四周边界距翼型表面的距离均为20倍的弦长。

使用Fluent6.3.26软件求解定常可压缩流动质量加权的N-S方程、能量方程和SST k-ω湍流模型和修正的Wilcox转捩模式。计算选用双精度求解器,方程的离散采用有限体积法,所有求解方程的对流项采用二阶迎风格式,扩散项采用中心差分格式,压力和速度耦合采用Coupled算法。翼型表面满足无滑移边界条件,远离翼型表面的区域设为压力远场边界条件。

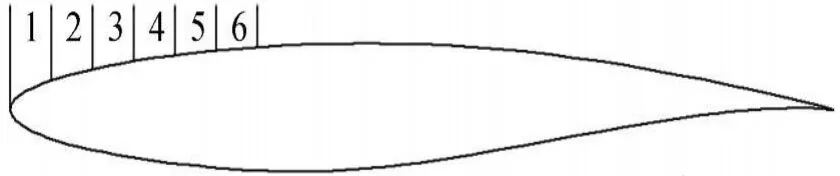
图1 RAE2822翼型吸气区分布示意图Fig.1 Schematic suction zone distribution for RAE2822 airfoil

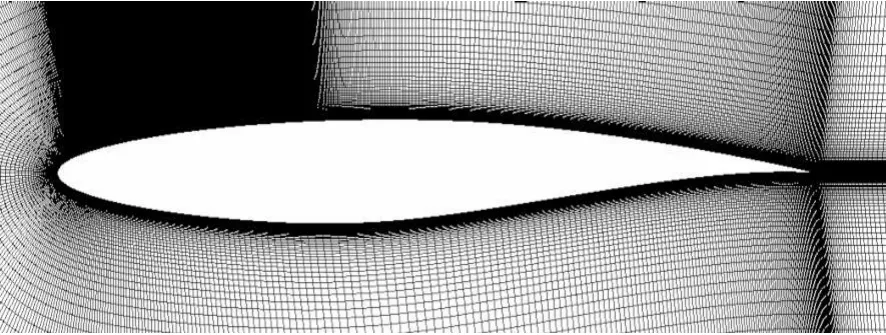
图2 翼型周围网格Fig.2 Grids around an airfoil

2 计算结果分析

2.1 数值计算与实验数据的比较

为了验证数值模拟结果的准确性,针对文献[8]中的实验数据,进行了数值计算对比验证分析。如图3所示,用于模拟的实体模型为弦长 1m的 NACA66012翼型,并在最大厚度位置插入一个长度为1m的平板。吸气区域在弦向方向为23%～42%的弦长长度范围,吸气孔直径为 0.1mm,孔间距为1mm。实验在英国南安普顿大学2m×1.5m低速风洞中进行,来流速度为20m/s,湍流度 Tu=0.1%,使用脉动压力传感器测量转捩位置。

图3 NACA66012翼型吸气控制示意图Fig.3 Sketch of suction control for an NACA66012 airfoil

图4给出了不同来流迎角下,数值计算和实验数据的对比曲线。图中横坐标为吸气系数(吸气平均速度与来流速度的比值),纵坐标为转捩位置增量(吸气控制下的转捩位置与吸气区域末端位置的流向坐标值之差)。由图中可以清楚地看出:数值计算与实验测量结果相比,转捩位置增量随吸气系数的变化规律基本保持一致;同一吸气系数下,计算和实验得到的转捩位置增量值吻合的较好。由此可见,本文数值模拟具有较好计算精度。采用的湍流模型以及转捩预报模式能较好地模拟吸气引起的转捩位置的变化规律,但是对转捩位置偏移量的模拟不够准确,还有待于对现有湍流转捩模式作进一步的修正。

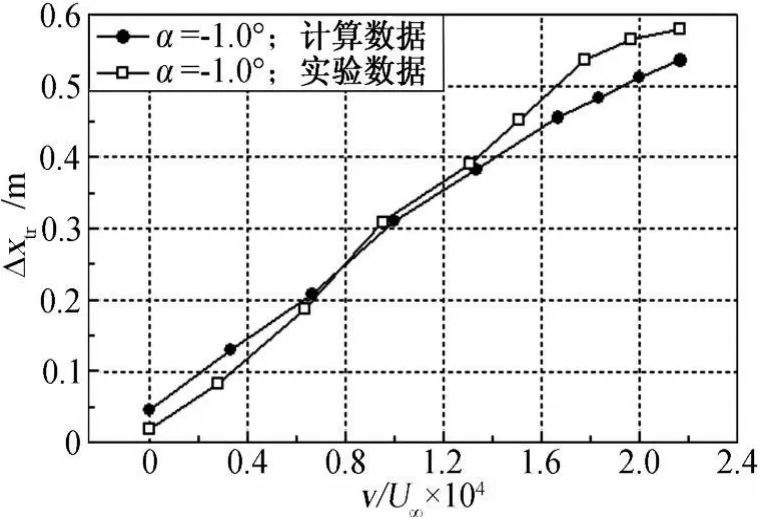
图4 NACA66012翼型吸气控制的计算与实验结果比较Fig.4 Comparison of the computational and experimental results forsuction control of the NACA66012 airfoil

2.2 孔径和孔间距的影响

表面开孔抽吸气控制的影响因素有很多,其中多孔面板的几何参数(孔的形状、孔的内外直径比、孔间距、孔隙率和孔的深度等)是主要影响因素。对于二维翼型吸气控制,这里我们只考虑孔径和孔间距这两个影响因素。计算来流马赫数Ma=0.3,Re=3.4×106,参照文献[9]中的实验研究结果,在吸气孔径小于0.3mm的条件下,当吸气速度小于最大吸气速度时,均可延迟转捩的发生,因此孔径和孔间距的选取如下:

(1)在孔间距L=10d的条件下,选取孔径d=0.06mm,0.1mm,0.2mm,0.3mm;

(2)在孔径d=0.1mm的条件下,选取孔间距L=10d,15d,20d,30d,40d。

在进行计算结果分析之前,首先定义一个无量纲的抽吸气系数,它表示单位时间内的质量流率,其表达式如下[10]:

其中:Q表示单位时间内穿过吸气孔被吸入的空气质量;b为展向长度;c为弦长;对于二维翼型,Q=ρsvsnd,这里 ρs为与吸气相关的密度,且 ρs=ρ∞ ;vs为吸气速度,n为吸气孔的个数,d为吸气孔直径;b=1。从而式(7)可写成以下形式:

2.2.1 孔径的影响

从计算结果得知,吸气孔径的变化会影响转捩位置和吸气控制的气动性能。在孔间距L=10d的条件下,当吸气系数为零时,跟表面未开孔的情况相比,随着孔径的增加,翼型边界层转捩位置向前有一个小的偏移量(见图5),这是由于表面开孔会使翼型表面的曲率发生改变,从而使边界层流动发生变化的缘故;当吸气系数不为零时,同一吸气系数下,孔径对翼型转捩位置偏移量的影响较小(见图6)。

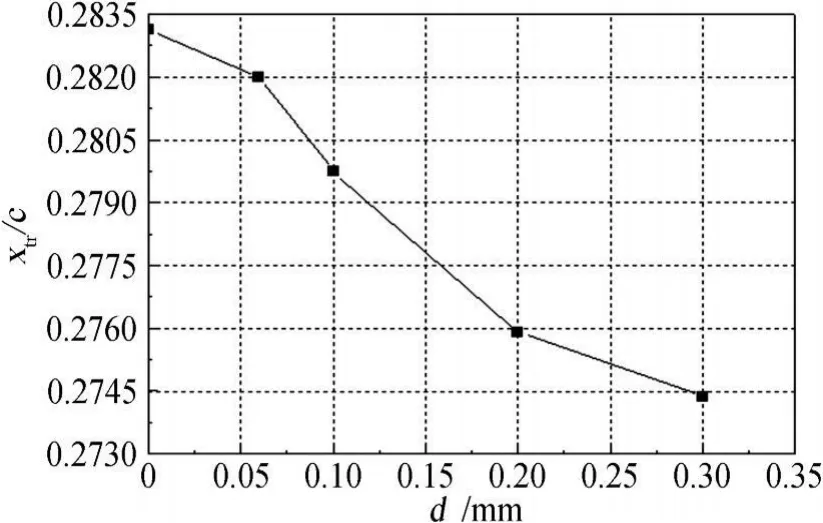
图5 翼型上翼面转捩位置随吸气孔孔径的变化规律Fig.5 Variation of transition positions with suction hole diameters on upper airfoil surface

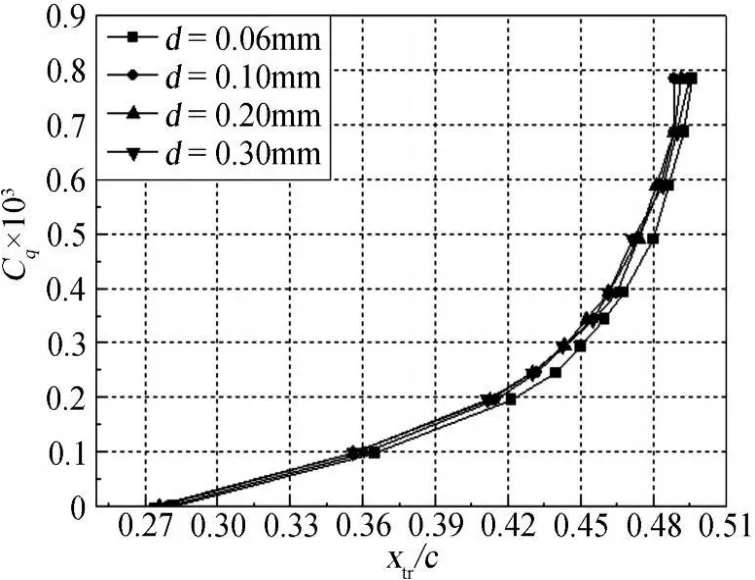
图6 不同孔径下,翼型上翼面转捩位置随吸气系数的变化规律Fig.6 Variation of transition positions on upper airfoil surface with suction coefficients at different hole diameters

由图7可知:不同孔径下,翼型总阻力随吸气系数的变化遵循同样的规律,即随着吸气系数的增大,翼型阻力呈先减小后增大的趋势;大孔径吸气控制下的阻力最小值较小,阻力恢复吸气系数逐渐较大,这里阻力恢复吸气系数定义为吸气控制下的阻力系数等于原阻力系数(未进行吸气控制)时所对应的吸气系数。由图8和图9可知,同一孔径下,随着吸气系数的增加,翼型摩擦阻力先减小后增大,压差阻力逐渐减小。在较大的吸气系数下,随着孔径的增大,摩擦阻力相对增加量逐渐减小,这是由于在同一吸气系数,且孔隙率相等的条件下,采用大孔吸气表面的孔数量较少,这样会减弱对吸气区内边界层流动的吸附作用,从而减弱对壁面剪切力的影响(见图10)。而随着孔径的增大,压差阻力相对减少量逐渐增大,故总阻力将减小。因此,采用大孔径进行吸气控制,总阻力随吸气系数的相对增加量较小,阻力恢复吸气系数也相对较大。

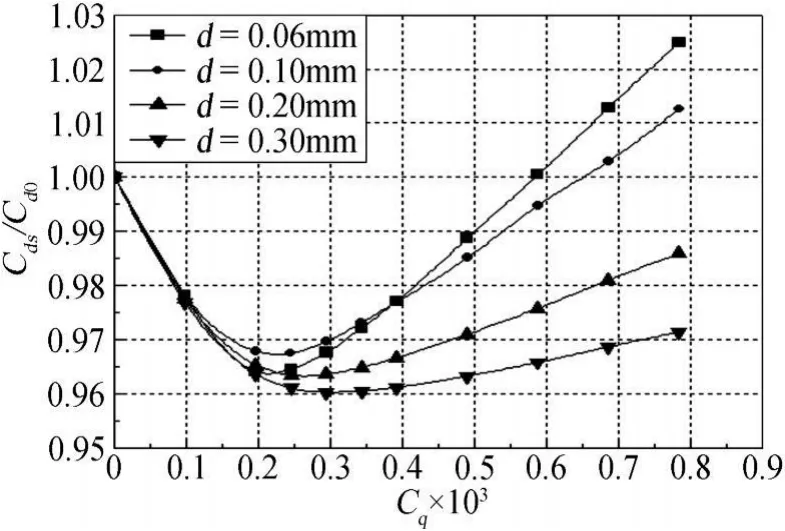
图7 不同孔径下,翼型阻力随吸气系数的变化规律Fig.7 Variation of airfoil drags with suction coefficients at different hole diameters

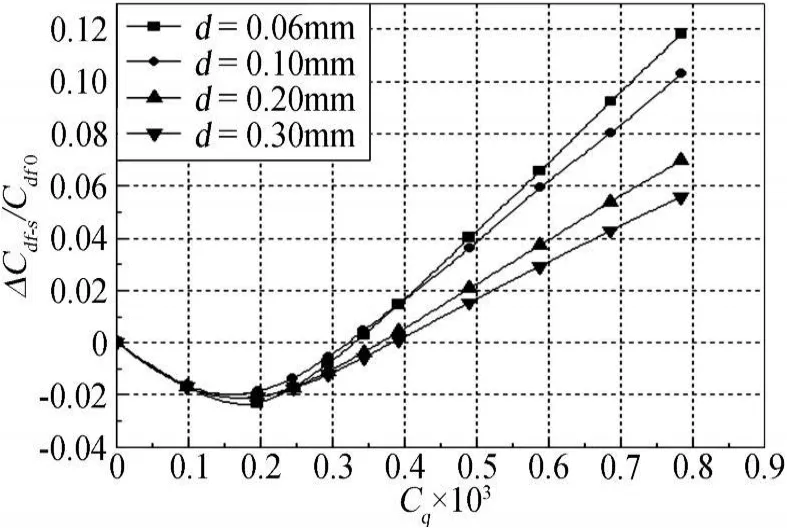
图8 不同孔径下,翼型摩擦阻力随吸气系数的变化规律Fig.8 Variation of airfoil friction drags with suction coefficients at different hole diameters

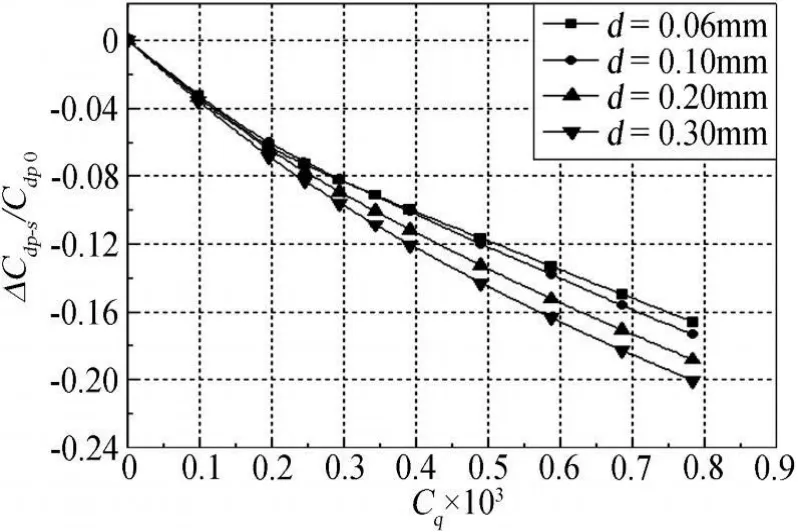
图9 不同孔径下,翼型压差阻力随吸气系数的变化规律Fig.9 Variation of airfoil pressure drags with suction coefficients at different hole diameters

2.2.2 孔间距的影响

计算结果表明,孔间距的变化对翼型吸气控制效果也有一定的影响。如图11所示,在同一吸气系数下,孔间距对翼型转捩位置的影响很微弱。但由图12可知,孔间距对翼型总阻力有较大的影响。在较大的吸气系数下,翼型总阻力的相对增加量随孔间距的增加而逐渐减小,阻力恢复吸气系数也随之增大。这归因于随着孔间距的增加,压差阻力相对减少量增大(见图14),摩擦阻力相对增加量反而减小的缘故(见图13)。这里摩擦阻力相对增加量随孔间距增大而减小的主要原因是:在同一吸气系数下,孔间距的增大导致吸气区孔隙率下降,从而使吸气对壁面剪切力影响区域缩小,即除了孔口边缘附近壁面剪切力较大外,远离吸气孔的壁面剪切作用相对较弱(如图15所示)。

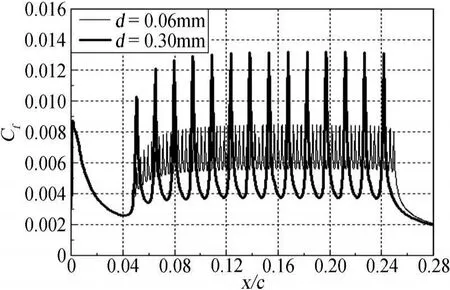
图10 不同孔径下,翼型上翼面表面摩擦系数随吸气系数的变化规律Fig.10 Variation of skin friction coefficients on upper airfoil surface with suction coefficients at different hole diameters

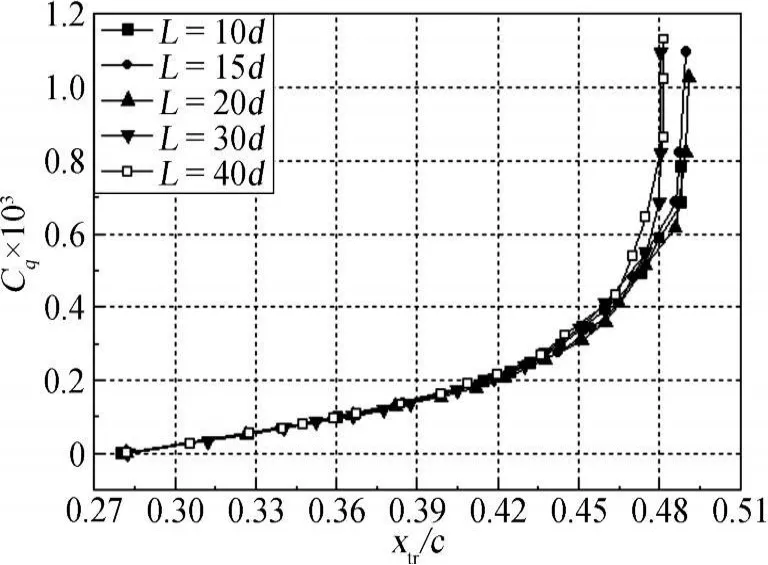
图11 不同孔间距下,翼型上翼面转捩位置随吸气系数的变化规律Fig.11 Variation of transition positions on upper airfoil surface with suction coefficients at different hole spacings

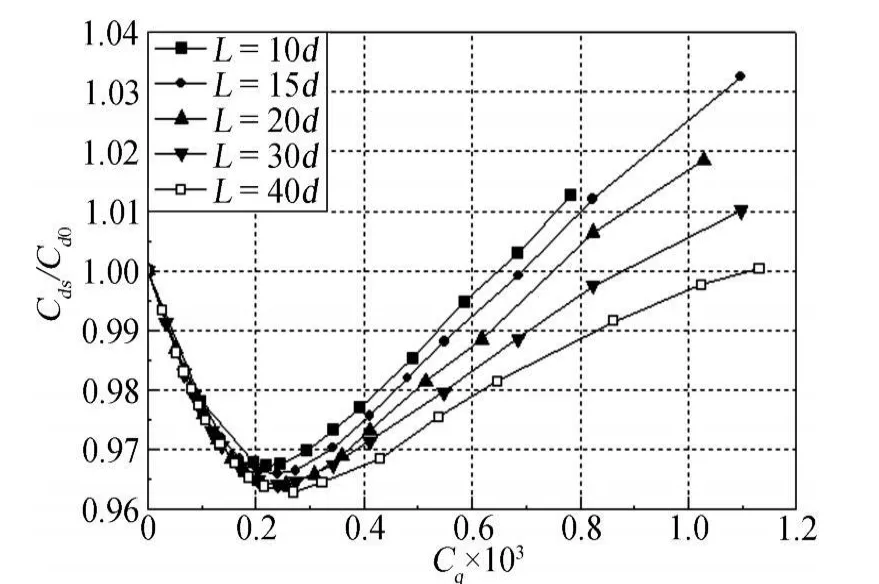
图12 不同孔间距下,翼型阻力随吸气系数的变化规律Fig.12 Variation of airfoil drags with suction coefficients at different hole spacings

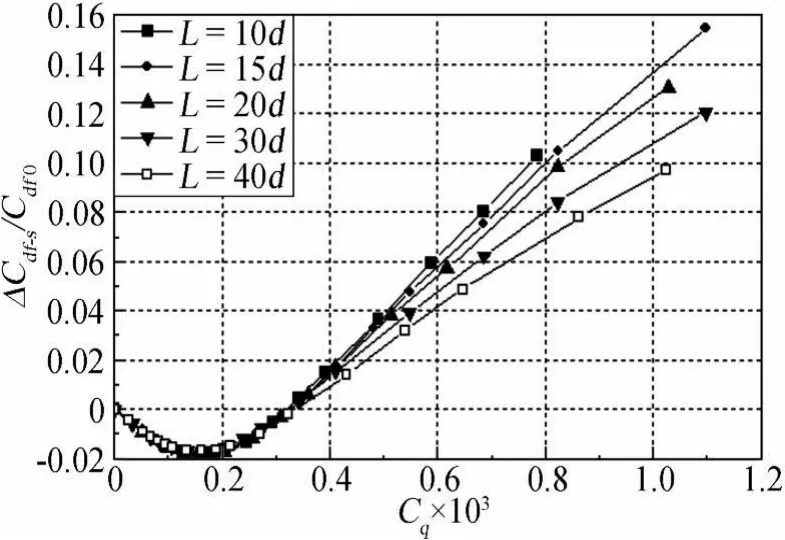
图13 不同孔间距下,翼型摩擦阻力随吸气系数的变化规律Fig.13 Variation of airfoil friction drags with suction coefficients at different hole spacings

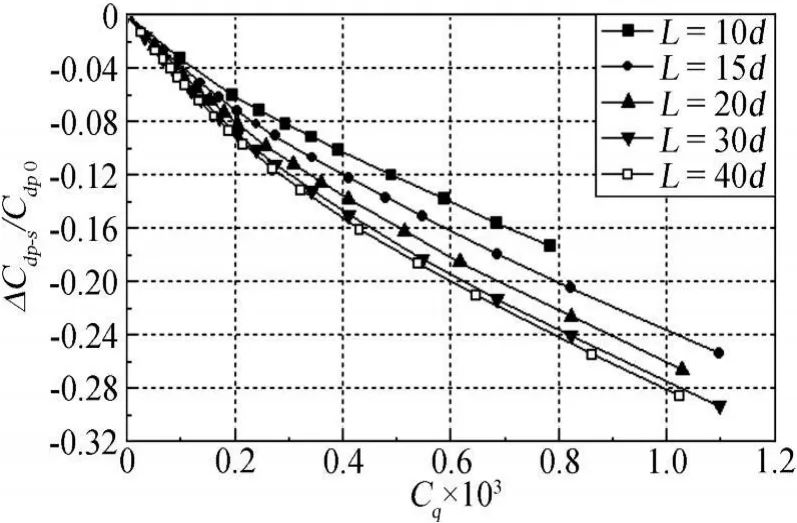
图14 不同孔间距下,翼型压差阻力随吸气系数的变化规律Fig.14 Variation of airfoil pressure drags with suction coefficients at different hole spacings

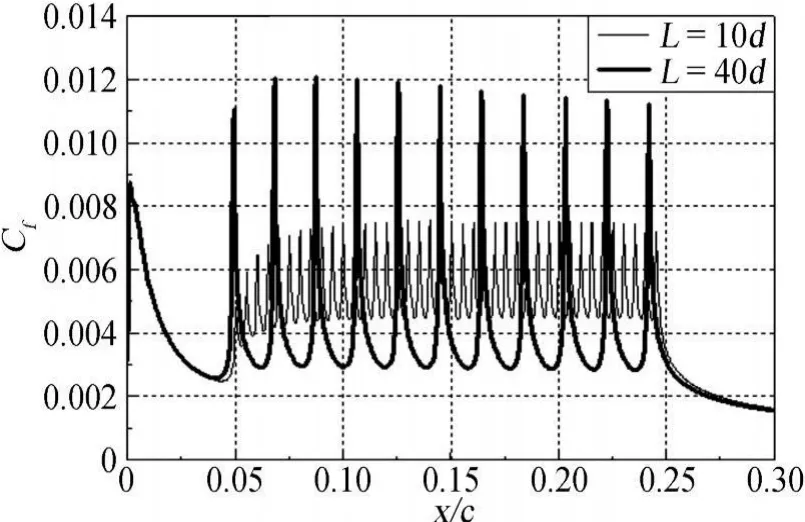
图15 不同孔间距下,翼型上翼面表面摩擦系数随吸气系数的变化规律Fig.15 Variation of skin friction coefficients on upper airfoil surface with suction coefficients at different hole spacings

2.3 吸气位置的影响

尽管抽吸气能有效地延迟边界层转捩的发生,但是层流流动控制的宗旨是使净阻力最小化,即以最小的抽吸气量,实现同样的减阻效果,这样能减少抽吸气系统的能量消耗和抽吸气的动量损失,从而使净阻力最小化。抽吸气量的影响因素有很多,其中抽吸气分布和吸气区位置是两个主要影响因素。关于抽吸气分布优化的研究,最具代表性的是英国南安普敦大学Nelson教授课题组对抽吸气优化设计进行的大量理论和试验研究工作[11-14]。这些研究主要是集中于平板边界层抽吸气优化设计,考虑在一个平板下面放置单个、两个或多个抽吸气板,预先给定一个理想的转捩位置,通过调节各个板的抽吸气系数使原转捩位置移至指定的位置,然后利用一个优化算法对抽吸气系数进行优化设计,使费用函数(抽吸气系数的平方和)达到最小值。而本文主要研究吸气位置的影响,参照1.2节的定义,吸气区位置分为以下几种情况:2-5(5%～25%弦长),3-5(10%～25%弦长),4-5(15%～25%弦长),5(20%～25%弦长)。计算的基于弦长的雷诺数和马赫数为Re=3.5×106,Ma=0.3,来流迎角均为0°,吸气孔直径为ds=0.1mm,孔间距Ls=1mm。

从图16可知,在同一吸气区位置的条件下,翼型转捩位置随吸气系数的变化遵循同样的规律,随着吸气量的增加转捩位置逐渐向后移动,并趋于一个固定不变的值;在中等吸气量下(Cq=0.2×103～0.6×103),吸气区域越小,转捩位置的向后偏移量越小。由图17可知,随着吸气区域不断缩小,并逐渐靠近自然转捩位置,翼型的阻力恢复吸气系数呈递增的趋势,这是由于在同一吸气系数下,采用较小的吸气区域进行控制,其对翼型表面剪切力的影响区域相对较小,从而对总摩擦阻力的影响也较小,且在吸气区域较小的情况下,翼型摩擦阻力随吸气系数的增加比较缓慢(见图18);而在同一孔径和孔间距下,吸气区域的大小对压差阻力的影响很微弱(见图19)。

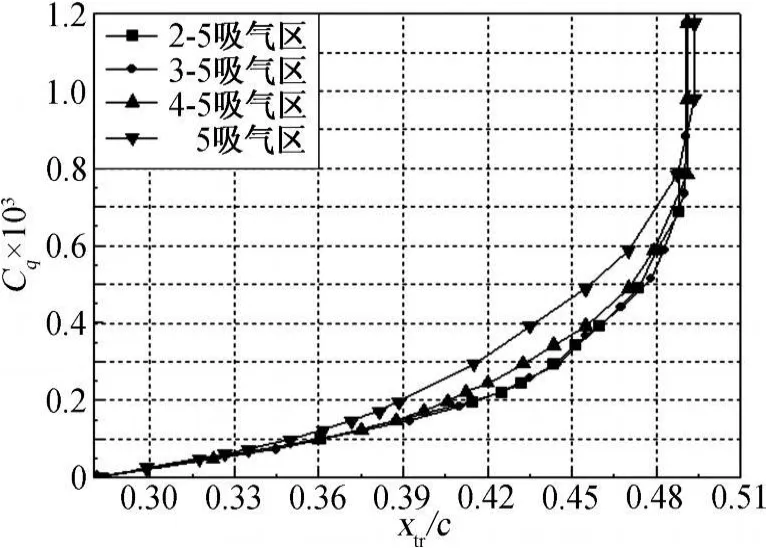
图16 不同吸气区域下,翼型转捩位置随吸气系数的变化规律Fig.16 Variation of transition positions on upper airfoil surface with suction coefficients at different suction areas

图17 不同吸气区域下,翼型阻力随吸气系数的变化规律Fig.17 Variation of airfoil drags with suction coefficients at different suction areas

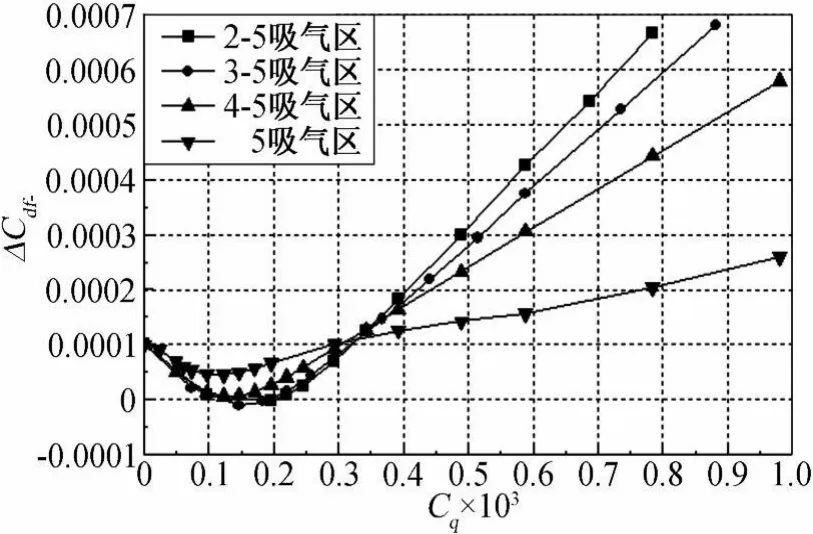
图18 不同吸气区域下,翼型摩擦阻力系数随吸气系数的变化规律Fig.18 Variation of airfoil friction-drags with suction coefficients at different suction areas

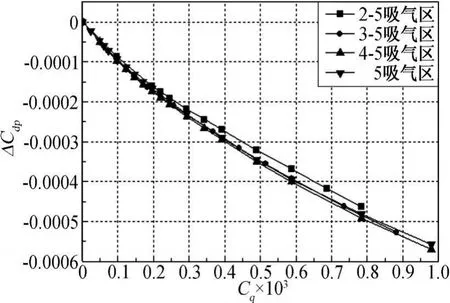
图19 不同吸气区域下,翼型阻力系数随吸气系数的变化规律Fig.19 Variation of pressure drag coefficients with suction coefficients at different suction areas

3 结 论

(1)修正的转捩预报模式能较好地模拟吸气引起的转捩位置的变化规律,但是对转捩位置偏移量的模拟不够准确,还有待于对其作进一步的修正;

(2)同一孔径和孔间距下,随着吸气量的增加,翼型转捩位置逐渐向后缘移动,并趋于一个固定不变的位置;

(3)孔径和孔间距的变化对翼型吸气控制效果都有一定的影响。采用较大的孔径和孔间距进行吸气控制会使翼型阻力恢复吸气系数增大,同时具有较低的相对阻力最小值;

(4)吸气区域越小,翼型的阻力恢复吸气系数越大。吸气区域的大小对压差阻力的影响较小,而对摩擦阻力的影响较为明显,且随着吸气区域不断缩小,其起始位置逐渐靠近自然转捩位置,翼型摩擦阻力随吸气系数的相对增加量越来越小。

[1]GREEN J E.Laminar flow control-back to the future[R].AIAA 2008-3738,2008.

[2]JOSLIN R D.Aircraft laminar flow control[J].Annual Review of Fluid Mechanics,1998,30(1):1-29.

[3]DENNING R M,ALLEN J E,ARMST RONG F W.Future large aircraft design-the delta with suction[J].AeronauticsJ ournal,1997,101(1005):187-198.

[4]WILSON R A L,JONES R I.Laminar flow for subsonic transport aircraft[J].Aerospace Engineering,1996,16(6):21-25.

[5]MACM AN US D G,EATON J A.Flow physics of discrete boundary layer suction-measurements and predictions[J].Journal of Fluid Mechanics,2000,417:47-75.

[6]MACM AN US D G,EATON J A.Measurement and analysis of the flow fields induced by suction perforations[J].AIAA Journal,1998,36(9):1553-1561.

[7]钱炜祺,詹浩.一种基于湍流模式的转捩预测方法[J].空气动力学学报,2006,24(4):502-507.(QIAN Weiqi,ZHAN Hao.Study of numerical method for flow transition prediction based on turbulence model[J].Acta Aerodynamica Sinica,2006,24(4):502-507.(in Chinese))

[8]WRIGHT M C M,NELSON P A.Wind tunnel experiments on the optimization of distributed suction for laminar flow control[J].Proceedingsof the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2001,215(6):343-354.

[9]ELLIS J E,POLL D I A.Laminar and laminarizing boundary layers by suction through perforated plates[R].Second European Forum on Laminar Flow Technology,Bordeaux,1996,8:17-26.

[10]BRASLOW A L,BURROWS D L.Experimental and theoretical studies of area suction for the control of the laminar flow boundary layer on an NACA 64A010 airfoil[R].NACA 1025,1951.

[11]NELSON P A,WRIGHT M C M.Automatic control of laminar boundary-layer transition[J].AIAA Journal,1997,35(1):85-90.

[12]RIOUAL J L,NELSON P A.Optimum drag balance for boundary-layer suction[J].Journal of Aircraft,1996,33(2):435-438.

[13]RIOUAL J L,NELSON P A.Experiments on the automatic control of boundary layer transition[J].Journal of aircraft,1994,31(2):1416-1418.

[14]VERES G V,T UTTY O R.Global optimization-based control algorithms applied to boundary layer transition problems[J].Control Engineering Practice,2004,12(4):475-490.