大跨斜拉桥主梁断面气动导纳的实测研究
2010-04-07廖海黎李明水徐洪涛
陶 奇,廖海黎,李明水,徐洪涛
(1.中国中铁二院工程集团有限责任公司,四川 成都 610031;2.西南交通大学风工程实验研究中心,四川 成都 610031;3.交通部公路科学研究院,北京 100088)
0 引 言
气动导纳的概念是由Sears[1]于1941年首先提出,并由Liepmann[2]于1952年应用到由紊流竖向脉动风引起的薄机翼抖振问题的研究中。1961年Davenport[3]开创性地把气动导纳的概念引入到了桥梁结构的抖振分析中。后来的研究人员也在Scanlan[4]的准定常抖振力表达式中引入气动导纳的概念,形成了Scanlan修正抖振力表达式。
由于桥梁断面的钝体性质和大气紊流的复杂性,气动导纳不再有类似机翼的理论解-Sears函数,而是与断面的形状、尺寸以及紊流特性有关,因此桥梁断面气动导纳需要通过风洞实验并结合适当的识别方法来确定。
根据测量抖振力方法的不同,将气动导纳的识别方法分为高频天平测力法、表面风压测量积分法和紊流场随机响应系统辨别法[5]。其中,前两种统称为直接测量法,后一种称为间接测量法。1984年,谢霁明[6]较早地开展了桥梁断面气动导纳识别方法的研究工作,但是他只是在理论上进行了公式的推导,并未有实验数据,从而无法验证其假设。1993年,李明水[7]利用高频测力天平和热线风速仪测量抖振力谱和风速谱识别了桥梁断面气动导纳,随后Sankaran[8]、顾巍[9]、靳新华[10]和赵林[11]等人采用同样的方法研究了桥梁断面气动导纳函数。1997年,Larose[12]采用节段模型测压的方式,直接测得表面力和力矩,结合Davenport抖振力谱公式计算得出了横风向气动导纳函数。Larose未对关于气动力矩的导纳函数进行测试,而后顾巍[9]、赵林[11]、马存明[13]和陈斌[14]等沿用类似的实验手段,进一步研究了气动导纳函数的多种影响因素。相对于直接测量法而言,间接测量法由于受仪器的精度等影响较大,故开展的较少。1998年,张若雪[15]采用紊流场节段模型的实验和确定性系统识别的方法识别了江阴长江大桥主梁断面的等效气动导纳函数,随后,秦仙蓉和顾明[16]采用随机系统识别法对桥梁断面的等效气动导纳函数进行了识别。
本文以苏通长江大桥为背景,研发了一套适合现场测压的装置,利用测压法对苏通大桥主梁断面的等效气动导纳函数进行了现场实测研究。
1 等效气动导纳的识别方法
对于气动导纳的识别研究,一般是在忽略脉动风互谱影响的基础上进行的。在Scanlan修正抖振力表达式中,对于顺、横风向抖振力和横风向抖振力矩各有2个、共6个气动导纳函数,其在频域内一般表述如式(1)~式(3):
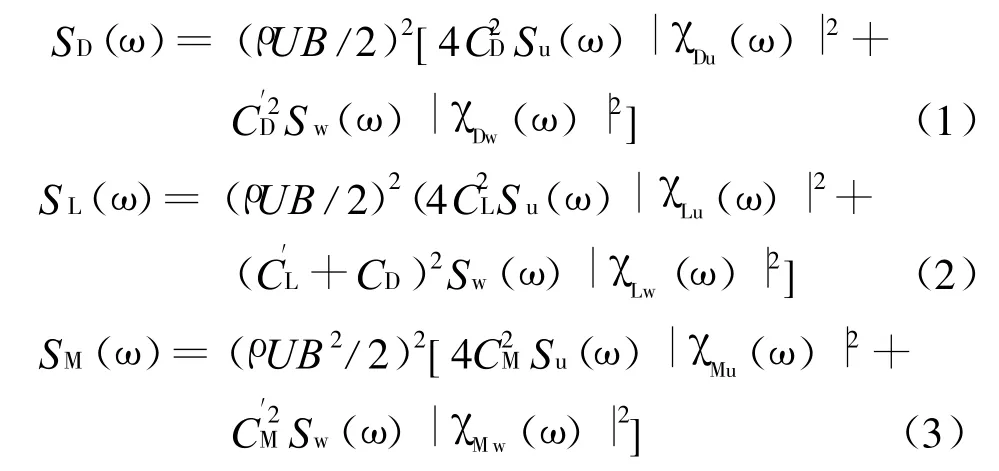
式中:χDu、χLu和 χMu表示顺风向的脉动风 u(x,t)和抖振阻力、抖振升力和升力矩之间在频域内的气动导纳函数 ;χDw、χLw和 χMw表示竖向脉动风 w(x,t)和抖振阻力、抖振升力和升力矩之间在频域内的气动导纳函数;SD(ω)、SL(ω)和 SM(ω)分别是抖振阻力谱、升力谱和升力矩谱;Su(ω)和Sw(ω)是纵向风速和竖向风速的功率谱;U为平均风速;ρ空气的密度;B为桥面宽度;CD、CL和CM分别为主梁断面的阻力、升力和升力矩系数和分别为阻力系数 、升力系数和力矩系数的斜率。
由于通过式(1)~式(3)来识别气动导纳有一定的困难,在大多数气动导纳的识别实践中[5,12-13,15-17],人们进一步假设:
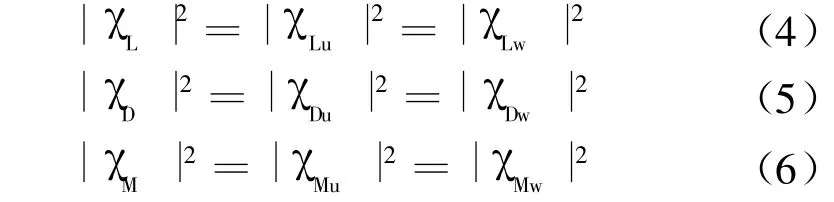
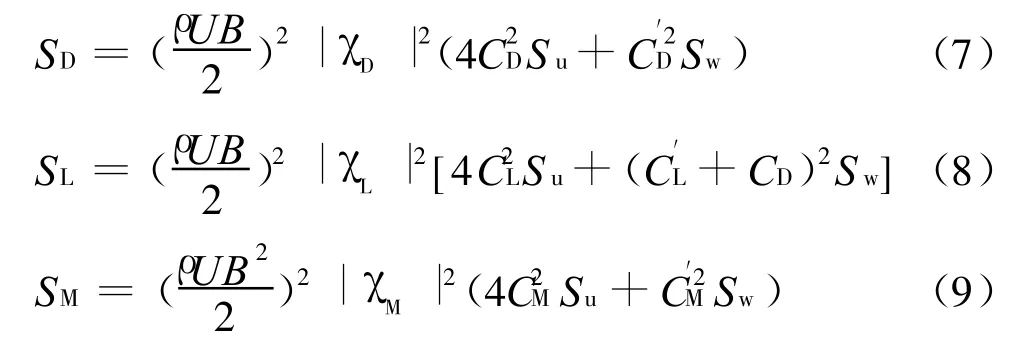
从式(7)~式(9)很容易导出等效气动导纳:
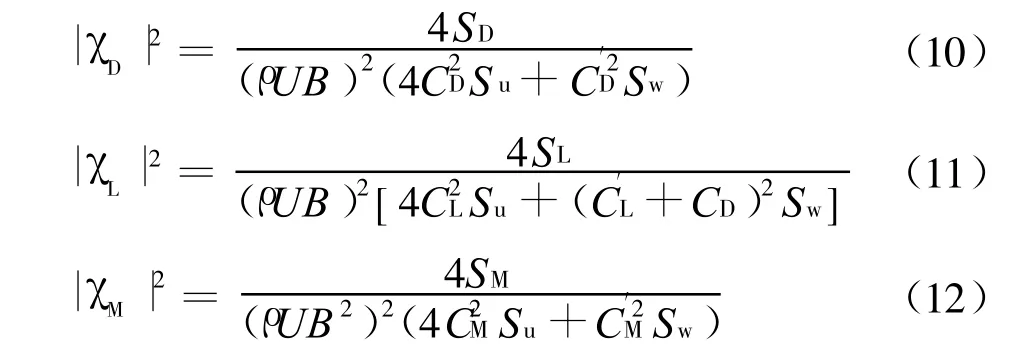
从式(10)~式(12)可以看出,只要同步测量了脉动风谱和脉动压力谱及断面静力系数,便可直接求出气动导纳。由于桥梁断面的等效气动导纳识别试验简单,数据处理方便,因此有着广泛的应用。
2 测量系统
2.1 同步脉动测压系统简介
现场测压所用的仪器是自行研制的60路同步动态测压系统,可以同时获得60个测压孔的静态和动态压力数据。压力传感器采用的是美国SM公司生产的SM-552型压力传感器。系统采用在信号调节器中加采样保持器的串行A/D工作方式。60路压力传感器和信号调节器输出的电信号经多路切换器变为2路模拟信号,由A/D转换为数字量存入工控机。同步信号驱动信号调节器中的采保电路,保证获得同一时刻的压力值。软件系统管理各部件的协调工作。
为了防水和合理地获取断面表面压力信号,特设计了一种π型压力感受器,如图1所示,其后接30cm的PVC管,另一头接入压力传感器。为了应对现场复杂的环境,保护压力传感器,为每个传感器做了一个保护装置,如图2所示。
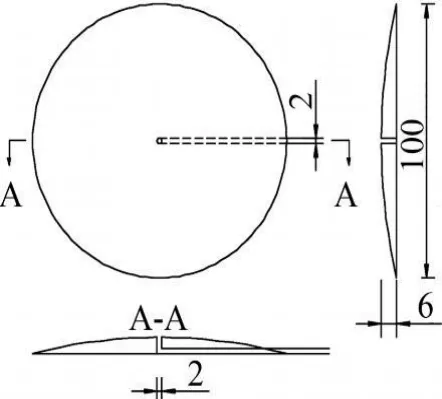
图1 π型压力感受器构造示意图(单位:mm)Fig.1 The π-type structure diagram baroreceptor(unit:mm)

图2 现场布置图Fig.2 The actually disposure
60路信号调节器做成二箱,每箱30路(其中一箱有10路接加速度计,压力传感器共用去50路),其中还包括压力传感器电源和多路切换器。其中放大倍数四挡可选择,滤波器截止频率二挡可供选择。同步控制器和A/D板置于工控机内。数据由工控机采集下来后,可以很方便地利用计算机进行数据分析处理。
实验前必须对系统进行标定。压力标定系统由多路接头、数字压力计和压力泵组成,完成对系统的检查、压力的传递和对系统的标定。系统的测压范围为-1000~+1000Pa,测量精度±1%,采样频率大于1000Hz。
测压系统中连接测压孔和传感器的是PVC塑料管道。由于测量的需要,PVC管道都具有一定的长度,当动态气流通过管道后,压力信号中的平均部分可以得到很好的传递,而脉动部分由于与管道的相互作用会发生畸变,从而导致脉动压力信号测量失真[18-19]。这种现象可以归结为测压管路的频率响应函数问题,即系统的输出端与输入端的脉动压力在频域上的比,在每个频率点上通常表现为复数形式,因而脉动压力的畸变可以用幅值和相位差的变化来表示。没有发生畸变的理想情况是脉动压力经过管道后在幅值上没有发生衰减或放大,并且相位差的变化与频率成线性关系(即任一频率的脉动压力信号都延迟一个固定的时间Δ t)。
为了使管路系统的频率响应函数在感兴趣的频率范围内接近没有发生畸变的理想情况,我们在管路中加限制器(阻尼器),这是改善测压管路系统频响函数的简单而直接的方法[13],它是在PVC管中加一些压扁铜管,从而限制脉动压力引起共振,达到改善实验效果的方法。在文献[13]中指出,在小于50Hz的频率范围内,通过压扁铜管的改善,即使在导气管总长60cm时,其频响的误差都比较小。频率范围超过50Hz之后,误差较大,特别是没有压扁铜管的频响曲线,即使管长才20cm,都会引起较大的误差。因此,如果保证导管总长不超过60cm,对于主要由脉动风中的低频部分所引起的桥梁抖振的脉动力,用它测量桥面的压力,其结果都能满足精度要求。
为了得到最佳效果,可以串联限制器的测压管路组成一个组合体系,本文是将三个阻尼器串联起来使用,如图3所示。
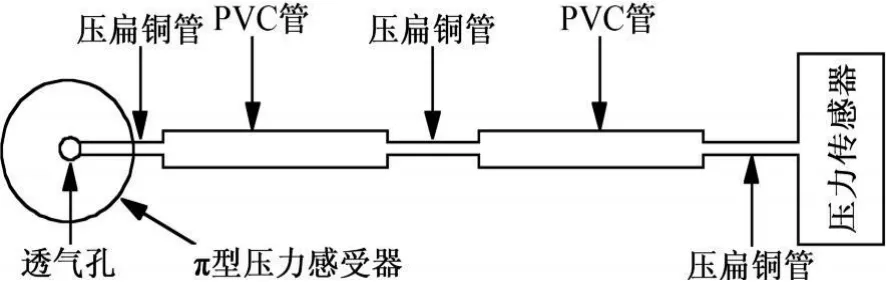
图3 测压管路布置图Fig.3 Pressure piping layout
2.2 脉动风速测量系统简介
为了识别气动导纳,须获取测压断面的同步脉动风速实测资料。我们在测压断面处,离桥面外边缘1.5m,高5m的位置设置了气象观测点,同步实测研究了该点的脉动风场。脉动风场观测仪器采用美国Young公司的 81000超声风速仪系统。Young-81000型三维超声风速仪具有很高的测量精度和良好的动态跟踪性能,环境温度在-50~50℃范围内,风速量程为-40~40m/s,分辨率0.01m/s,测量精度±1%±0.05m/s(0~30m/s)。
3 工程背景及测点布置
苏通长江大桥主桥为一座7跨钢箱梁斜拉桥,主跨为1088m,主桥跨度布置为100m+100m+300m+1088 m+300m+100m+100m。桥塔为混凝土结构,塔高为300.4 m。主梁为带风嘴的闭口钢箱梁,梁高为4.0m,主梁总宽度为41.0m,该桥的总体布置如图4所示。
测压法要求布置的测点尽量多,这样通过压力积分得到的抖振力才更加准确。然而由于受到空间位置的限制和采集系统的限制(计算机内存,硬盘大小的限制),不可能布置太多的测点,综合了以上因素,最后确定沿跨中桥梁断面表面布置50个测压点,风嘴部分平均相邻孔距为0.5m,其余部位平均相邻孔距为2m,如图5所示(另一边对称布置),测压断面距离北塔329.3m。

图4 苏通大桥总体布置(单位:m)Fig.4 General layout of Su-tong Bridge(unit:m)
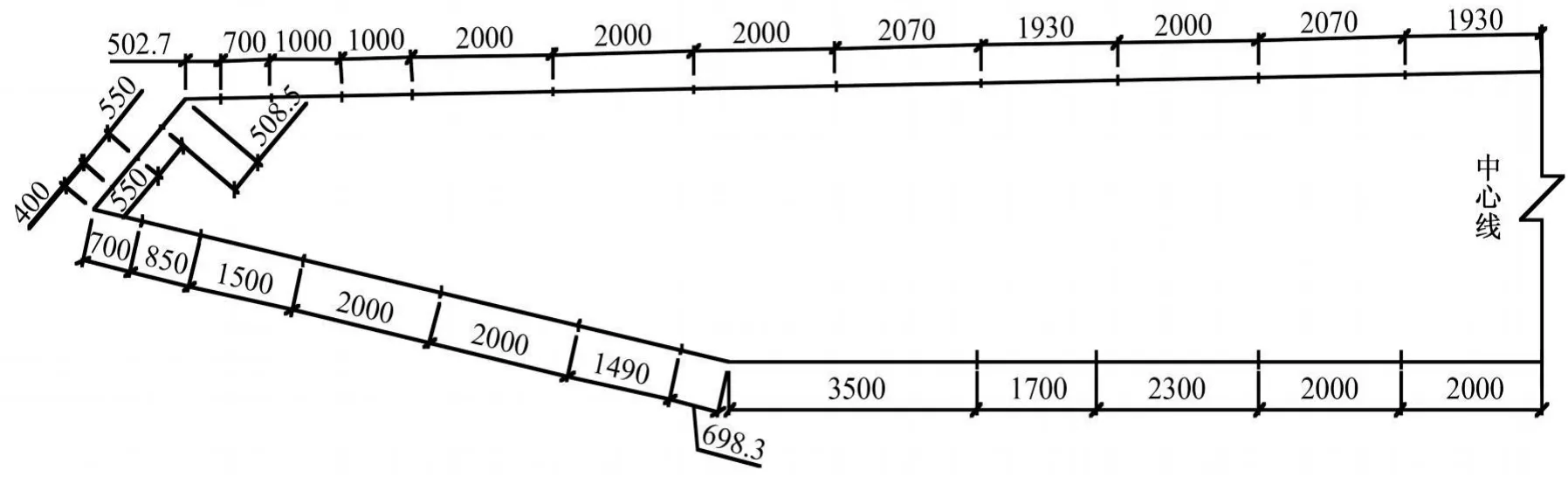
图5 断面测点布置图(单位:mm)Fig.5 Measure point distribution(unit:mm)
4 测量结果及分析
笔者在2007年5月~2007年8月这3个月时间内对苏通大桥的主梁断面气动力进行了实时监控,从同步的风速数据分析结果来看,强风方向与桥轴线垂直的情况很少见。为了利用现有的抖振分析理论(目前斜风理论还不成熟,研究的较少)及对比风洞实验的结果,本文从所得结果中只选择了2个风偏航角较小的时间段来进行分析,紊流风特性参数如表1所示,计算时风速时程长度选取了10min。
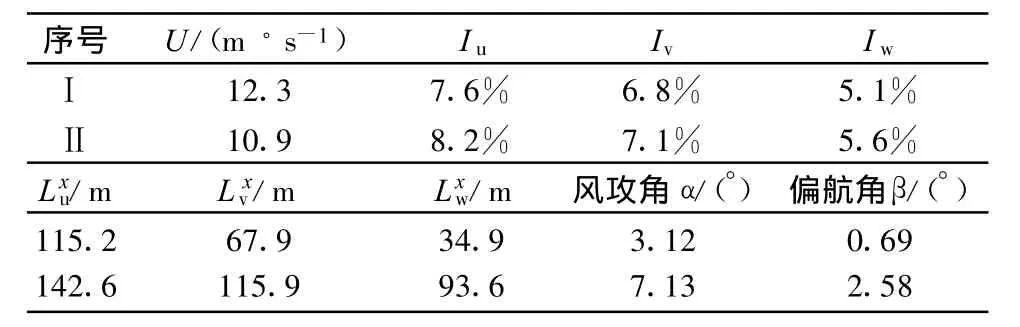
表1 紊流风特性参数Table1 Characteristic parameters of turbulent wind
风洞实验中,采用了尖塔紊流场来模拟表1中风场紊流风特性参数的实测值(紊流度精确模拟,积分尺度仅保证 L/B接近)。刚体测压模型的比尺为1∶80。测点同样采用图5的布置方法进行布置。风洞实验设置了 7 个攻角,分别是 7°、5°、3°、0°、-3°、-5°和-7°。现场识别气动导纳函数所用的参数(如紊流风谱和三分力系数等)均来自于实测。在图6和图7中分别给出了苏通大桥主梁断面气动导纳函数的现场实测结果、风洞实验结果和对应的经验曲线。

图6 攻角3.12°时各气动导纳Fig.6 Aerodynamic admittance at attack angle 3.12°
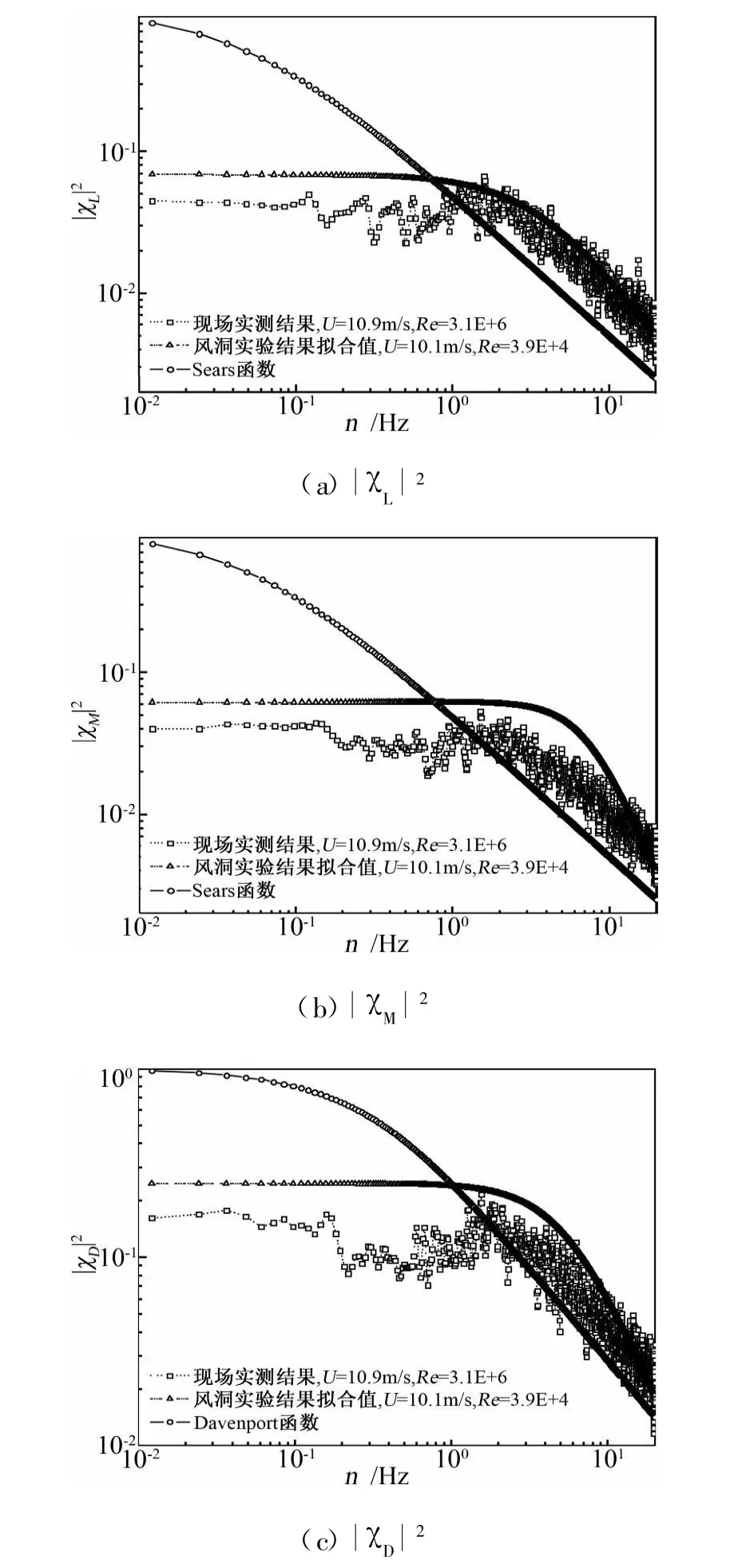
图7 攻角7.13°时各气动导纳Fig.7 Aerodynamic admittance at attack angle 7.13°
从图6和图7中可以看出:现场实测结果与风洞实验结果比较接近,略小于风洞实验值,表明雷诺数对苏通大桥主梁断面气动导纳函数影响较小(现场雷诺数约为实验室雷诺数100倍)。攻角对气动导纳函数有一定的影响,随攻角增大,气动导纳函数值随之增大。这可能是由于攻角的增大使得截面变得相对较钝,增大了尾流的脱落、再附和畸变,从而对气动导纳的大小产生了影响。现场实测结果和风洞实验结果与经验曲线有交叉,在低频范围内现场实测结果略小于风洞实验结果,远小于经验值,曲线变化较为平缓,在高频范围内现场实测结果和风洞实验结果与经验值逐渐靠拢,现场实测结果介于经验值和风洞试验结果之间,三者有相同的变化趋势。因此,用Sears函数和Davenport经验公式作为主梁断面的气动导纳函数在低频范围内显然高估计了结构所受到的抖振荷载,因此计算的结果将偏于保守。
5 结 论
通过以上分析,可以得出如下几点结论:
(1)实测得到的气动导纳函数与缩尺比为1∶80的模型风洞实验结果接近,雷诺数对苏通大桥主梁断面气动导纳函数的影响较小,风洞实验结果具有一定的可靠性;
(2)攻角对气动导纳函数有一定的影响,随攻角增大,气动导纳函数值随之增大;
(3)用Sears函数和Davenport经验公式作为桥梁断面的气动导纳函数在低频范围内高估计了结构所受到的抖振荷载,计算结果偏于保守,因此,对大跨桥梁进行抖振响应分析时,应针对气动导纳函数进行专门的实验研究。
[1]SEARS W R.Some aspects of non-stationary airfoil theory and its practical application[J].Journal of the Aeronautical Sciences,1941,8:104-108.
[2]LIEPMANN H W.On the application of statistical concept to the buffeting problem[J].Journal of the Aeronautical Sciences,1952,19(12):793-800.
[3]DAVENPORT A G.Buffeting of suspension bridge by storm winds[J].J.ASCE.S T3,1962,88(6):233-268.
[4]SCANLAN R H.The action of flexible bridges under wind,Ⅱ:buffeting theory[J].J.Sound and Vibration,1978,60(2):201-211.
[5]项海帆.现代桥梁抗风理论与实践[M].北京:人民交通出版社,2005.
[6]XIE J,et al.Identification of aerodynamic admittance functions for bridge road decks[A].Proc.Of The 2nd Asia-Pacific Symposium on Wind Engineering[C].Beijing,1989:618-628.
[7]李明水.连续大气湍流中大跨度桥梁的抖振响应[D].[博士论文].成都:西南交通大学,1993.
[8]SANKARAN R,JANCAUSKAS E D.Direct measurement of the aerodynamic admittance of 2-D rectangular cylinders in smooth and turbulent flows[J].J.Wind Engrg And Indusl Aerodyn,1992,41-44(1):601-611.
[9]顾巍.钝体和桥梁断面的气动导纳实验技术与研究[D].上海:同济大学,2000.
[10]靳欣华.桥梁断面气动导纳识别理论及实验研究[D].[博士论文].上海:同济大学,2003.
[11]赵林.风场模式数值模拟与大跨桥梁抖振概率评价[D].[博士论文].上海:同济大学,2003.
[12]LAROSE G L,TANAKA H,GIMSING N J,et al.Direct measurement of buffeting wind forces on bridge decks[J].Journal of Wind Engineering and Industrial Aerodynamics,1997,74-76:809-818.
[13]马存明.流线箱型桥梁断面三维气动导纳研究[D].[博士论文].成都:西南交通大学,2007.
[14]陈斌.识别气动参数的测压法实验研究[D].[博士论文].上海:同济大学,2006.
[15]张若雪.桥梁断面气动参数识别理论和实验研究[D].[博士论文].上海:同济大学,1998.
[16]秦仙蓉,顾明.桥梁结构气动导纳识别的随机子空间方法[J].同济大学学报,2004,32(4):421-425.
[17]蒋永林.斜拉桥抖振响应分析[D].[博士论文].成都:西南交通大学,2000.
[18]谢壮宁,顾明,倪振华.复杂测压管路系统动态特性的通用分析方法[J].同济大学学报(自然科学版),2003,31(6):702-708.
[19]王维新,谢壮宁.测压传压管路系统动态特性的实验分析[J].西北大学学报(自然科学版),2005,35(4):702-708.
