碳纤维材料单层索网非线性主共振的特性

杨立军,吴 晓,罗佑新,孙 晋

(湖南文理学院土木建筑工程学院,湖南常德 415000)

0 前言

单层钢丝索网体系是点支式柔性支承玻璃幕墙结构中的一种新型体系,以其建筑结构简捷、轻盈美观、通透性好等优点深受建筑师的青睐,应用广泛[1-2]。但是钢拉索耐腐蚀性差,钢拉索索网维护成本高,为了提高结构的耐久性,本来使用在宇宙、航空领域的碳纤维等新材料开始了实验性的应用。与钢拉索相比,碳纤维索具有耐久性好、不锈蚀、无磁性、强度重度比高等优点,而且徐变和松弛等重要指标均优于钢索,弹性模量选择范围大、温度变形小,虽然还存在高价和剪切强度低等缺点,但随着碳纤维索的产量增加和新的锚固技术开发应用,不少问题已逐渐得到解决[3]。碳纤维材料作为房屋、桥梁的加固材料已得到了相当广泛应用,而碳纤维作为拉索首先在桥梁结构得到了实践。如已经建造了一些小跨径的全部或部分CFRP拉索的人行斜拉桥,一些学者对应用碳纤维索的大跨度斜拉桥结构的静、动力行为开展了研究[3-4]。碳纤维索在屋盖支承体系的应用目前还没有相关报道。碳纤维索作为一种很有应用前景的材料,可以预见在不远的将来,将会很快推广应用到屋盖支承体系中。国内外一些学者对柔性索网结构的动力特性开展了非常多的研究[5-11],文献[5]研究了单层索网非线性自振特性,文献[8-10］研究了单层索网动力特性,文献[11]研究了碳纤维索网的非线性自振特性,但是,至今未见到研究碳纤维单层索网非线性共振的文献。因此,本文研究了碳纤维单层索网的非线性主共振特性。

1 索网主共振近似解

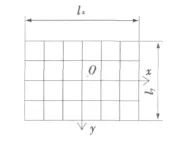
图1 单层索网

图1为单层索网,为了研究其非线性主共振特性,做如下基本假设:(1)索网的索是理想柔性的;(2)索的变形是小垂度的;(3)索材料满足虎克定律。由弹性振动理论知,单层索网在外激励作用下的非线性振动方程为:

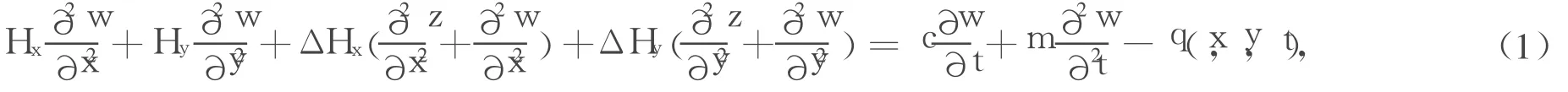
式中:Hx(或Hy)为索网x(或y)方向单位宽度内索拉力水平分量初值;ΔHx(或ΔHy)为索网x(或y)方向单位宽度内索拉力增量水平投影;z(x,y)为索网初始形状函数;w(x,y,t)为索网的振动位移函数; q(x,y,t)为作用在索网上的外激励;c为索网的阻尼系数;m为索网的单位面积质量。

以图1所示单层索网中心O为坐标原点,由弹性理论可知索网的拉力增量ΔHx、ΔHy分别为:

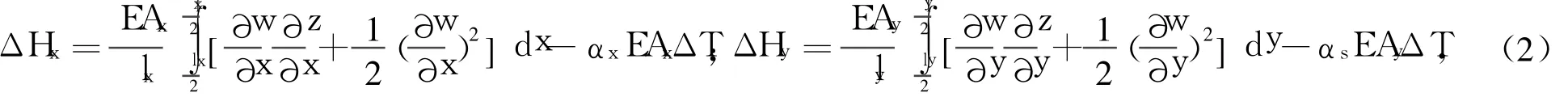
式中:E为索网材料的弹性模量;Ax、Ay分别为x、y方向单位长度内索网的横截面积。

该索网初始状态下的曲面形状函数z(x,y)、索网的振动位移w(x,y,t)及外激励q(x,y,t)分别为:

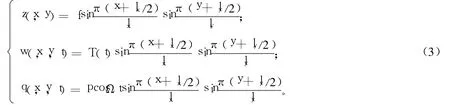
把式(2)、(3)代入式(1)中,利用伽辽金原理可以得到下式:

式中:a为振幅;φ为相位角;T1(a,φ,Ωt)、T2(a,φ,Ωt)为角φ周期函数,周解为2π,而a、φ是时间的慢变函数,设由下列对时间的微分方程确定:

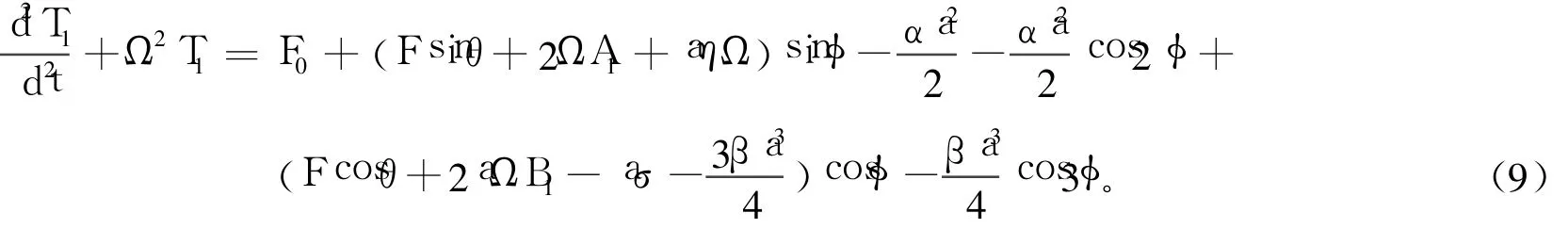
由式(9)可以求得:

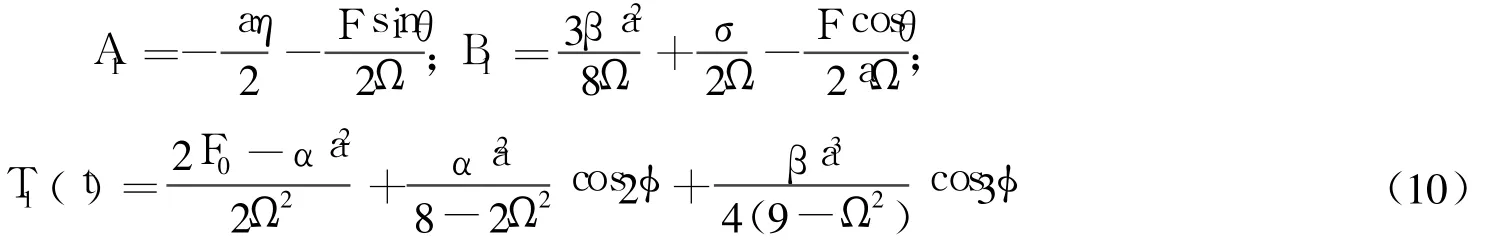
由以上有关各式可得索网的振动位移函数为:

把式(10)代入式(7)中且令a′=0,θ′=0可以得到索网主共振幅频响应方程和相频响应方程为:

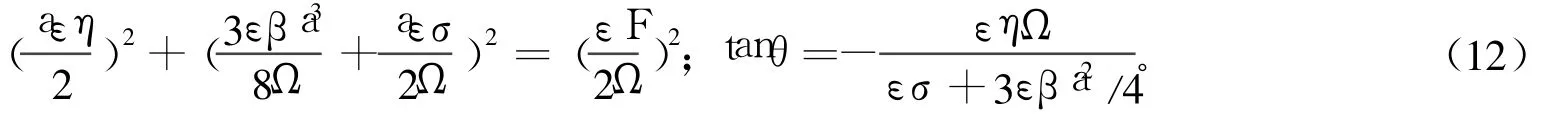
2 算例分析

为讨论碳纤维索网的非线性共振特性,以便把碳纤维索网与钢丝索网进行比较研究,采用中关村文化商厦 30m×70 m点式幕墙平面钢丝索网支承体系为参照物,按照等轴向刚度准则、等强度准则分别构造了碳纤维索网。该平面钢丝索网ly=70m,lx=30 m,x向索截面面积62mm2,索初始张拉力Fx= 320 kN,间距2m;y向索截面面积336 mm2,初始张拉力Fy=120 kN,间距1.67 m。得需要的基本参数为:Hx=3.2×105N/(2m)=1.6×105N/m;Hy=1.2×103N/(2m)=7.2×104N/m; Ax=6.72×10-4m2/(2m)=3.36×10-4m;Ay=3.36×10-4m2/(1.67 m)=2.01×10-4m。

单层索网的构造参数见表1。其中:1#为钢丝索网;2#为与1#等截面的碳纤维索网;3#为按照等轴向刚度准则构造的碳纤维索网;4#为按照等强度准则构造的碳纤维索网。4种结构相同的计算参数为: ly=70m;lx=30 m;Hx=1.6×105N/m;Hy=7.2×104N/m。

表1 结构材料和截面特性

为比较表1中4种单层索网主共振特性,令阻尼比ξ=c/(2mω0),取ξ=2%,温度增量ΔT=40℃,外激励幅值P=0.3 kN/m2,把有关参数代入式(12)第一分式中,即可得到单层索网幅频曲线,如图2所示。

为分析温度增量对索网主共振特性影响,取ξ=2%;P=0.3 kN/m2,ΔT分别取0℃、40℃,由式(12)得到 1#索网、3#索网幅频曲线,如图3所示。

为分析阻尼对索网主共振特性影响,取ΔT=40℃,P=0.3 kN/m2,阻尼比ξ分别取2%、5%,由式(12)得到 1#索网、3#索网幅频曲线,如图4所示。

为分析外激励幅值对索网主共振特性影响,取 ΔT=40℃;ξ=2%,外激励幅值 P分别取0.15 kN/m2、0.3 kN/m2,由式(12)得到1#索网、3#索网幅频曲线,如图5所示。

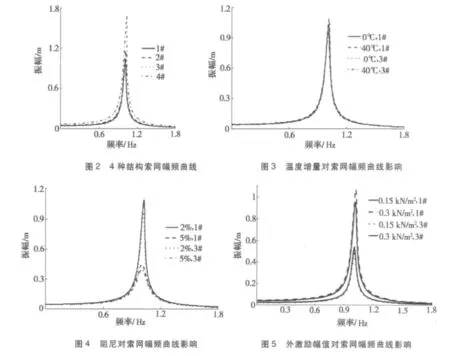
(1)当阻尼、外激励、温度一定时,随着谐调参数的增大索网的共振区域及振幅也增大,2#、4#索网的共振区域及振幅均大于 1#索网的共振区域及振幅,3#索网的共振区域及振幅则小于1#索网的共振区域及振幅,这表明横截面积较小的索网具有起振速度快、振幅大的特点,且按照等轴向刚度准则设计的碳纤维索网的共振区域及振幅均最小。

(2)当阻尼及外激励一定时,温度升高会使索网的共振区域及振幅增大,钢丝索网的共振区域及振幅大于按照等轴向刚度准则设计的碳纤维索网的共振区域及振幅。且钢丝索网与碳纤维索网相比,其共振区域及振幅受温度的影响更大些。

(3)外激励及温度一定时,索网的共振区域及振幅受阻尼的影响较大,随着阻尼的增大索网的共振区域及振幅减小的很快,但是按照等轴向刚度准则设计的碳纤维索网的共振区域及振幅低于钢丝索网的共振区域及振幅。

(4)当阻尼及温度一定时,索网的共振区域及振幅受外激励的影响较大,随着外激励的增大索网的共振区域及振幅增大得很快,但是按照等轴向刚度准则设计的碳纤维索网的共振区域及振幅低于钢丝索网的共振区域及振幅。

通过以上分析可知,当轴向刚度相同时,碳纤维索网抗振性能优于钢丝索网。

3 结论

考虑温度变化及几何非线性影响,研究了碳纤维材料单层索网的非线性主共振问题。采用连续化理论导出了碳纤维材料单层索网在外激励作用下的振动控制方程,采用Galerkin原理及KBM法求得了碳纤维材料单层索网的非线性主共振近似解及对应的定解。

随着谐调参数增大、温度升高、阻尼变小、外激励增大,索网的共振区域及振幅增大。在相同条件下,按照等轴向刚度准则设计的碳纤维索网的共振区域及振幅低于钢丝索网的共振区域及振幅,这表明当轴向刚度相同时,碳纤维索网抗振性能优于钢丝索网。

[1]Vyzantiadou M,Avdelas A.Point Fixed Glazing Systems:Technological and Morphological Aspects[J].Journal of Constructional Steel Research,2004,60(8):1227-1240.

[2] Schlaich J,Schober H,Moschner T.Prestressed Cable Net Facades[J].Structural Engineering International,2005,15(1): 36-39.

[3] 苟昌焕,谢 旭,高金盛,等.应用碳纤维索的大跨度斜拉桥静力学特性分析[J].浙江大学学报:工学版,2005,39 (1):137-142.

[4] 谢 旭,高金盛,苟昌焕,等.应用碳纤维索的大跨度斜拉桥结构振动特性[J].浙江大学学报:工学版,2005,39 (5):728-733.

[5] 尚仁杰,李 谦,吴转琴,等.基于最小能量原理的矩形平面预应力索网结构大变形自由振动研究[J].振动与冲击,2007,26(9):158-161.

[6] 姚国红,刘树堂,康丽萍.单榀张弦桁架结构各因数的影响分析[J].河南科技大学学报:自然科学版,2008,29(2): 65-68.

[7] 杨立军,吴 晓,孙 晋.玻璃采光顶预应力索桁架支承体系固有振动[J].河南科技大学学报:自然科学版,2009, 30(5):49-53.

[8] 吴丽丽,王元清,石永久.点支式玻璃建筑单层索网体系的动力特性分析[J].重庆建筑大学学报,2006,28(3):39-42.

[9] 冯若强,花定兴,武 岳,等.单层平面索网幕墙结构玻璃与索网协同工作的动力性能研究[J].土木工程学报, 2007,40(10):27-33.

[10] 洪天华,李宏男.风荷载作用下单层平面索网体系点支式玻璃幕墙的动力性能研究[J].防灾减灾工程学报, 2008,28(2):156-162.

[11] 吴 晓,杨立军,孙 晋,等.碳纤维材料双层索非线性自振的温度响应[J].西安建筑科技大学学报:自然科学版,2008,40(2):155-160.