一类复合函数的广义凸性
2010-03-27贲天璐李东升魏彦吉
贲天璐, 李东升,2*, 魏彦吉,2, 陆 晶,2, 王 洋
(1.长春工业大学基础科学学院,吉林长春 130012;2.吉林农业大学发展学院,吉林长春 130600)
0 引 言
推广凸规划中的重要结果,一个主要的方面是将涉及的凸函数推广为各种意义下的广义凸函数,伪凸函数和拟凸函数是凸函数的两种重要的推广,它们在全局优化理论中有重要的应用[1-4]。文中主要讨论一类复合函数的伪凸和拟凸性。首先为伪凸函数、严格伪凸函数、拟凸函数、严格拟凸函数和强拟凸函数定义,然后为利用相关定义证明复合函数在一定条件下的伪凸性、严格伪凸性、拟凸性、严格拟凸性及强拟凸性,并给出了若干例子[5-8]。
1 预备知识
定义1[1]令X⊂Rn是一非空开凸集,f:X→R1是一可微的实值函数。
1)如果对任意两点x1,x2∈X,满足

时,都有f(x1)≥f(x2),则称 f是X中的伪凸函数。
2)如果对任意两点x1,x2∈X,且 x1≠x2,满足

时,都有f(x1)>f(x2),则称 f是X中的严格伪凸函数。
其中,▽f是f的梯度。
定义2[1]令X⊂Rn是一非空开凸集,f:X→R1是一实值函数,如果对任意两点 x1,x2∈X及任意λ∈(0,1)有

则称 f是X中的拟凸函数。
定义3[1]令X⊂Rn是一非空开凸集,f:X→R1是一实值函数,如果对任意两点x1,x2∈X,且f(x1)≠f(x2)及任意λ∈(0,1)有

则称 f是X中的严格拟凸函数。
定义4[1]令X⊂Rn是一非空开凸集,f:X→R1是一实值函数,如果对任意两点x1,x2∈X,且x1≠x2及任意λ∈(0,1)有
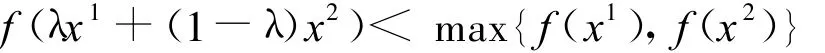
则称 f是X中的强拟凸函数。
2 主要结果
定理1 设 f(x)为X⊂Rn上的伪凸函数,φ(y)是R上的单调增函数且可微,则复合函数h(x)=φ[f(x)]是X上的伪凸函数。
证明 由题意,对任意x1,x2∈X,如果

则由φ′(y)≥0,知

再由f(x)的伪凸性知

从而有

即

故
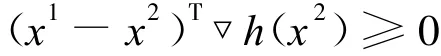
成立时,都有

定理2 设f(x)为X⊂Rn上的严格伪凸函数,φ(y)是R上的严格单调增函数且可微,则复合函数h(x)=φ[f(x)]是X上的严格伪凸函数。
证明 由题意,对任意x1,x2∈X,且x1≠ x2,如果
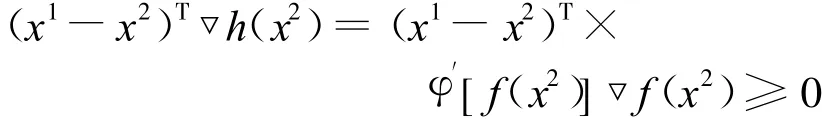
由φ′(y)≥0,知

再由 f(x)的严格伪凸性知

从而

即

故

成立时,都有

定理3 设 f(x)为X⊂Rn上的拟凸函数,φ(y)是R上的单调增函数,则复合函数h(x)= φ[f(x)]是X上的拟凸函数。
证明 由题意,对任意 x1,x2∈X及任意λ∈(0,1),总有
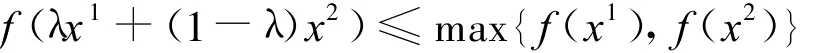
则
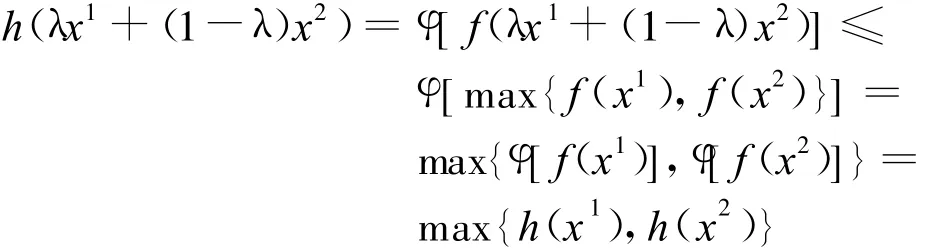
即

定理4 设f(x)为X⊂Rn上的严格拟凸函数,φ(y)是R上的严格单调增函数,则复合函数h(x)=φ[f(x)]是X上的严格拟凸函数。
证明 由题意,对任意两点x1,x2∈X,且f(x1)≠f(x2)及任意λ∈(0,1)有

则

即

定理5 设f(x)为X⊂Rn上的强拟凸函数,φ(y)是R上的严格单调增函数,则复合函数h(x) =φ[f(x)]是X上的强拟凸函数。
证明 仿定理4证明即可。
3 举 例
例1 已知f(x)=-lnx,X⊂Rn,φ(y)=ey,y∈R1,则复合函数h(x)=φ[f(x)]是X上的伪凸函数。
证明 由题意,对任意x1,x2∈X,如果

则由φ′(y)=ey≥0,知

由f(x)的伪凸性可知

从而有

即

故

成立时,都有

例2 已知 f(x)=lnx,X⊂Rn,φ(y)=ey,y∈R1,则复合函数h(x)=φ[f(x)]是X上的严格伪凸函数。
证明 由题意,对任意x1,x2∈X,且x1≠x2,如果

由φ′(y)=ey≥0,知
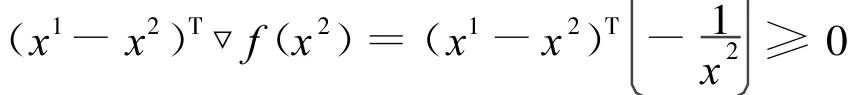
再由 f(x)的严格伪凸性知

从而有
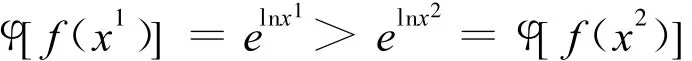
即

故

成立时,都有

例3 已知f(x)=-x,X⊂Rn,φ(y)= lny,y∈R1,则复合函数h(x)=φ[f(x)]是X上的拟凸函数。
证明 由题意,对任意 x1,x2∈X及任意λ∈(0,1),总有
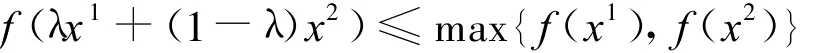
则

即

例4 已知f(x)=x,X⊂Rn,φ(y)=lny,y∈R1,则复合函数h(x)=φ[f(x)]是X上的严格拟凸函数。
证明 由题意,对任意两点x1,x2∈X,且f(x1)≠f(x2)及任意λ∈(0,1),总有
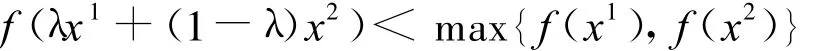
则
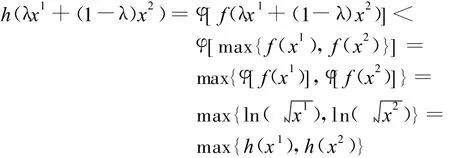
即

例5 已知 f(x)=ex,X⊂Rn,φ(y)=lny,y∈R1,则复合函数h(x)=φ[f(x)]是X上的强拟凸函数。
证明 由题意,对任意两点x1,x2∈X,且x1≠x2及任意λ∈(0,1),总有
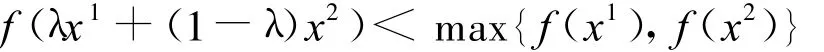
则
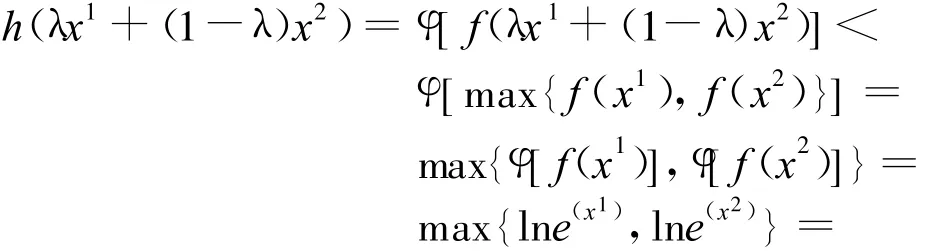

即

4 结 语
广义凸函数在最优化理论中有重要的应用。文中对单调函数和复合函数的广义凸性进行了讨论,得到了相关的结论。关于广义凸函数中更多的性质还需进一步研究。
[1] 林锉云,董加礼.多目标优化的方法与理论[M].长春:吉林教育出版社,1992.
[2] 魏权龄,闫洪.广义最优化理论和模型[M].北京:科学出版社,2003.
[3] 韩继业,修乃华,戚厚铎.非线性互补理论与算法[M].上海:上海科学出版社,2006.
[4] 郭科,陈聆,魏友华.最优化方法及其应用[M].北京:高等教育出版社,2007.
[5] 旷华武,阳南宁.线性空间中的一类新广义凸集及其应用[J].西南师范大学学报:自然科学版,2010,35(4):1-5.
[6] HU Qing-jie,XIAO Yun-hai,CHEN Nei-ping. Optimality and duality on fractional multi-objective prorammily under semilocal E-convexity[J].数学季刊:英文版,2009,24(2):200-210.
[7] 黄志传.一类广义凸多目标分式规划的最优性条件和对偶[J].广东教育学院学报,2009,29(5):44-50.
[8] 李瑞华,王雪梅.广义凸规划问题的最优性条件[J].绵阳师范学院学报,2010,29(2):15-18.
