速度选择器参数设计及其中子光学特性
2010-03-24孙良卫李新喜谢超美朱成银
彭 梅 孙良卫 陈 良 李新喜 谢超美 朱成银
(中国工程物理研究院核物理与化学研究所 绵阳 621900)
一般而言,中子小角散射实验需用长波长(λ=0.3−2 nm)单色中子,其波长展宽应很小(Δλ/λ=5%−30%),具体数值来源于实验要求,但由速度选择器设计参数所限制。对欲得到近乎平行入射中子光束的中子小角散射谱仪,由白光中子源或一定波段的冷中子获取单色中子束的最常用方法,是用机械速度选择器。它是对中子不透明的圆柱形转子,示意图见图1。
我国的中子小角散射技术尚处于起步阶段,速度选择器加工未见相关报道。本文用基于蒙特卡洛方法的Vitess程序对速度选择器作模拟计算,以优化其设计参数,并对经速度选择后的中子作光学特性分析。

图1 中子速度选择器示意图Fig.1 Schematics of the rotor-type velocity selector of neutrons.
1 速度选择器透过中子波长和分辨率
设速度选择器长度为L,表面片螺旋角为Φ,转子角速度为ω,则平行于其旋转轴线入射的白光中子束中,只有波长满足公式(1)条件的中子才能通过,从而对入射中子单色化[1]:

式中,h=6.62×10−34m2·kg/s为普朗克常量,m=1.67×10−27kg为中子质量。
设速度选择器转子半径为R,螺旋片间缝隙宽度为d,则单色中子的分辨率为:
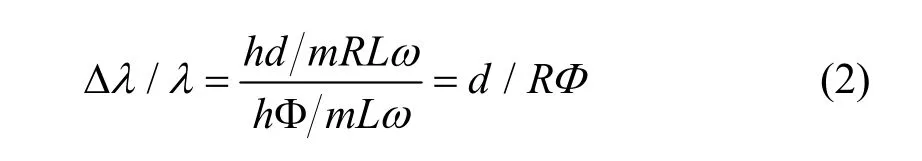
2 速度选择器参数设计计算
我们用蒙特卡洛方法的 Vitess程序[2]计算不同参数的速度选择器模型,模型的中子源为20 K的矩形冷中子包,其尺寸为120 mm(h)×50 mm(w),出口中子通量为 6.0×106cm–2·s–1,冷中子包至导管入口的间隙为1 m,直传输导管长2 m,导管内壁超镜因子为1.5,速度选择器与导管出口对接,导管横截面为100 mm(h)×30 mm(w),速度选择器另一侧开中子窗,尺寸也为100 mm(h)×30 mm (w),导管横截面中心与速度选择器中子窗中心位于同一高度。
2.1 选择器长度的优化计算
若其他参数固定,速度选择器转子长度就是在一定时间里的中子飞行距离,则该转子长度决定了中子速度也即波长,同时,经该转子选择的中子要有足够的通量。
速度选择器长度优化的计算参数为:转子半径R=180 mm;缝隙宽度d=0.53 mm;螺旋角Φ=32°;中子窗中心半径r=150 mm;转速为12000 r/min。图2(a)为中子波长λ随转子长度L而变化的模拟结果,λ随L增大而呈渐近线递减。计算中考虑了中子重量在飞行过程中对中子轨迹的影响,计算考虑中子重量在飞行过程中对中子轨迹的影响,同时因为飞行过程中散射到速度选择器以外的中子数量非常小(<0.1%),不影响优化计算结果,计算中对此部分中子忽略不计。由图2(b)结果可知,中子通量随转子长度变化基本呈高斯曲线分布,半高宽为239.3 mm,L=368.4 mm时中子通量最大。

图2 转子长度与选择波长(a)和中子通量(b)Fig.2 Wavelength (a) and neutron flux (b) v.s.the length of rotor.
2.2 转子表面片螺旋角的设计
转子螺旋角Φ反映中子飞行路径中前后两个缝隙的角度差异,螺旋角Φ越大,前后缝隙的角度差异越大。速度选择器Φ设计时输入参数为:转子半径R=180 mm;转子长度L=420 mm;缝隙宽度d=0.53 mm;中子窗半径r=150 mm;转速为12000 r/min。用Vitess程序计算了螺旋角对选择波长的影响,计算结果见图3(a)。从图3(a),随转子螺旋角Φ增大,选择的波长变大,波长与转子螺旋角Φ基本上成线性关系。从计算结果数据中还可得到中子通量与螺旋角Φ函数关系,绘成曲线图3(b)。曲线进行多项式拟合,得到中子通量最大时候的螺旋角Φ。

图3 螺旋角与选择波长(a)和中子通量(b)Fig.3 Wavelength (a) and neutron flux (b) v.s.helix angle.
3 中子光学特性
3.1 中子输运函数
采用两个探测器,分别放置在速度选择器前后,使速度选择器转子相对束流中心线偏转,偏转角度范围为−4°~+4°,其中负角度为转子螺旋角相反方向,正角度则为转子螺旋角一致方向[3]。设旋转速度12000 r/min,得到各波长中子在速度选择器前后计数分别为 N0和 N1,则速度选择器的中子输运效率为[4]:

图4(a)为束流发散度分别为1°、0.5°、0.2°和0.01°时的速度选择器输运效率,速度选择器转子中心轴线相对中子束中心线偏转为0°。图4(b)为转子倾角分别为−4°、−2°、0°、2°和4°时速度选择器输运函数。对曲线积分得中子通量值,并对0°倾角的通量作归一化,倾角−4°、−2°、2°和4°下选择器后的中子通量分别为0.16、0.68、0.92和0.70。

图4 不同束流发散度(a)和不同转子倾角(b)下输运函数Fig.4 Transfer efficiency at different divergency (a) and tilt angle(b).
3.2 速度选择器常数与波长分辨函数
速度选择器常数 C=λω=hΦ/(mL)仅与螺旋角Φ和转子长度L相关。其对任何转速和波长是常量,但随速度选择器转子倾角α变化,模拟计算结果见图5(a),当α=−4°~+4°,C基本随α线性增大。
波长分辨函数随转子倾角的变化曲线见图5(b),当α=−4°~+4°、 源中子束发散度为0.01°、0.2°、0.5°和 1°时,波长分辨率均随α增大而变好,但发散度越大,选择得到的中子束波长分辨率变差。
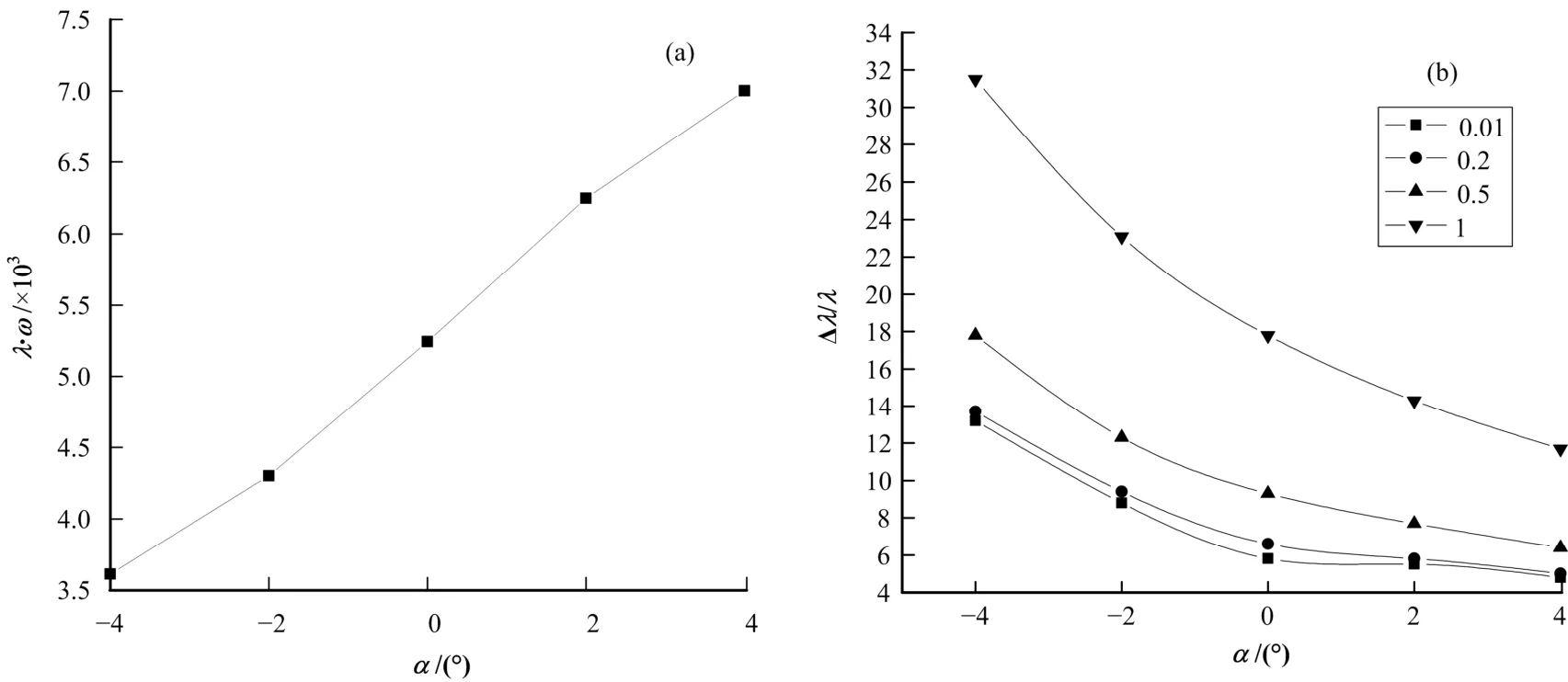
图5 速度选择器常数(a)和波长分辨(b)与转子倾角关系Fig.5 Velocity selector constant (a) and wavelength resolution (b) v.s.the tilt angle.
4 结果与讨论
速度选择器选择的波长与转子长度成反比,与转子螺旋角成正比。可视所需波长设计速度选择器转子长度和表面片螺旋角,同时应考虑中子通量值来对设计的参数进行优化。本文的在转速 12000 r/min、转子半径R=180 mm、中子窗半径r=150 mm、缝隙宽度d=0.53 mm等条件下优化得到的速度选择器转子长度L=340−380 mm和螺旋角Φ=34°。
(1) 中子通量与转子长度关系呈高斯分布,中心为 368.4 mm,但曲线顶部较平,转子长度为340−380 mm均可得最大中子通量。
(2) 中子通量与螺旋角关系曲线进行多项式拟合得到:

由此可求得,螺旋角Φ=34°时的中子通量最大。若速度选择器转速为1000−12000 r/min,转子倾角为−4°~+4°,由式(1),中子波长的选择范围为0.1−5 nm。
经速度选择器后中子光学特性表明,源中子发散度对中子输运函数影响很大。发散度为 0.01°的中子束,经过速度选择器后的中子输运效率可达70%;发散度为1°的中子束输运效率仅50%左右(图4a)。而且,相对于发散度小的输运函数曲线,发散度大的输运函数曲线的底部更发散。0.01°发散度中子束输运函数曲线的底部宽度为~0.05 nm,但发散度为 1°的中子束输运函数曲线底部宽度接近 0.1 nm,速度选择器的单色性能变差。
由图4(b),转子倾角从−4°增至4°,输运函数曲线向右移动,选择波长变大;转子不倾斜的时候输运函数峰高而狭窄,转子倾斜角度变大,输运函数曲线有不同程度展宽,曲线峰高普遍下降。倾角对中子通量影响明显,−4°、−2°、2°和4°倾角的归一化中子通量分别为0.16、0.68、0.92和0.70,−4°时中子通量最低。
转子倾角与速度选择器常数关系分析(图 5(a))表明,转速一定的情况下,倾角越大,速度选择器常数越大。这是因为大的倾角相当于增大了转子螺旋角Φ,因此可选择更长的波长,从而使速度选择器常数增大,这和图4(b)的转子倾角和选择器输运函数关系研究结果相洽。
转子倾角对选择的波长和波长分辨有明显影响(图5(b)),倾角从−4°向+4°变化,选择波长变大,波长分辨率变好。结合源中子束发散度研究发现,在0.01°发散度时,最好分辩可达到5.0%左右,而在1°发散度时,分辩最差达到32%左右。
因此,基于本文的计算模型和输入参数,用Vitess软件,通过对速度选择器参数的优化计算,得到优化后的参数,包括速度选择器长度L和转子螺旋角参数Φ。通过对速度选择器后面中子光学特性模拟计算,研究和分析了转子倾角和源中子束发散度对中子光学特性的影响,并得到了相应影响关系的函数、曲线和重要的光学特性参数值。基于本文的输入条件,发现转子倾角和源中子发散度对速度选择器以后中子光学特性影响明显,速度选择器设计时应充分考虑这些因素以获得合适的设计指标,开展中子小角散射实验研究时则应恰当选择转子倾角以满足实验需要。
1 丁大钊, 叶春堂, 赵志祥, 等.中子物理学.北京: 原子能出版社, 2005.545−546 DING Dazhao, YE Chuntang, ZHAO Zhixiang, et al.Neutron physics.Beijing: Atomic Energy Press, 2005.545−546
2 www.hmi.de/projects/ess/vitess/
3 Rosta L, Fuzi J, Homanyi L.Physica B, 2006, 385−386:1283−1286
4 Rosta L, Fuzi J, Homanyi L.Physica B, 2004, 350: 711
