基于中心差分卡尔曼滤波器的快速SLAM算法

田 翔，张 亮，陈耀武

(浙江大学数字技术及仪器研究所，浙江杭州310027，cyw@mail.bme.zju.edu.cn)

移动机器人同时定位与地图创建 SLAM (Simultaneous Localization and Mapping)问题［1－2］是指在未知环境中移动机器人利用自身定位信息创建环境地图，同时利用已创建的环境地图进行自身定位.经过十多年的研究和发展已经产生了许多SLAM算法，典型的包括基于扩展卡尔曼滤波的SLAM算法(EKF-SLAM)，基于粒子滤波器的SLAM算法(FASTSLAM1、FASTSLAM2)，基于稀疏信息矩阵滤波器的SLAM算法(EIF-SLAM)等［3－8］.由于在EKF-SLAM中状态向量和状态向量协方差都需要维护所有已检测的路标，因此在路标密集环境下SLAM速度很慢，从而限制其在实际中的应用.另外由于机器人SLAM中的预测过程和测量过程都是非线性模型，所以在EKFSLAM算法中使用了一级泰勒展开中对预测过程和测量过程进行线性近似，但是当非线性方程的非线性严重时会导致EKF-SLAM算法的一致性出现问题［9］.在FASTSLAM中SLAM的速度和一致性受粒子数目的影响，粒子数目过小可能导致SLAM结果发散，粒子数目过多会导致SLAM速度太慢从而限制其在实际中的应用.

本文提出基于中心差分卡尔曼滤波器的快速SLAM算法对预测过程和测量过程的线性近似精度上进行了改进，使用Stirling插值方法可以对非线性过程近似到二级泰勒展开，从而提高SLAM的精确性，并且使用已检测过的路标统计信息对由已检测路标和机器人位置组成的状态向量和状态协方差矩阵进行动态调整，以保证它们的大小限制在固定范围内，从而提高了SLAM速度.本文算法同EKF-SLAM和FASTSLAM进行分析发现在内存占用上要优于EKF-SLAM和FASTSLAM.通过对在稀疏路标环境和密集路标环境下的SLAM结果进行比较表明在SLAM精确性和一致性上都优于FASTSLAM2.0算法.

1 中心差分卡尔曼滤波器SLAM

中心差分卡尔曼滤波器是一种对非线性过程使用Stirling多项式插值公式近似，同时将其和卡尔曼滤波器结合所组成的滤波器.基于此滤波器对移动机器人进行SLAM称为CDKFSLAM.

1.1 Stirling多项式插值

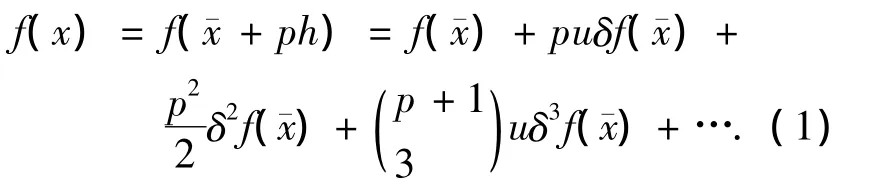
式中:u和δ分别为操作符.

对于式(1)如果只考虑到二级近似而忽略之后的所有高阶项则可以简化为

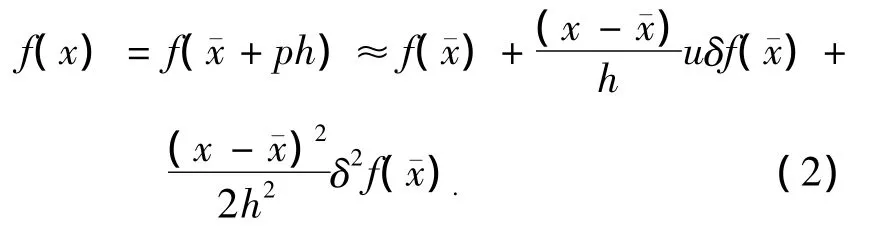
式(2)中操作符u和δ的定义为

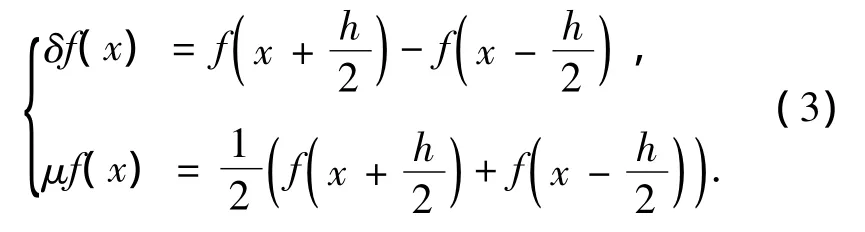
对式(2)中的操作符使用式(3)进行替换可得

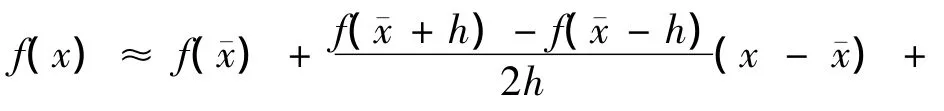
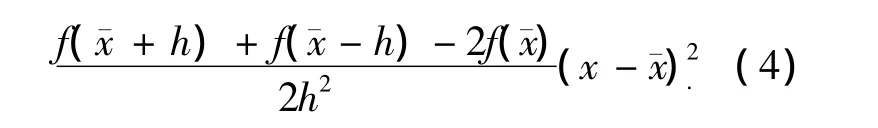
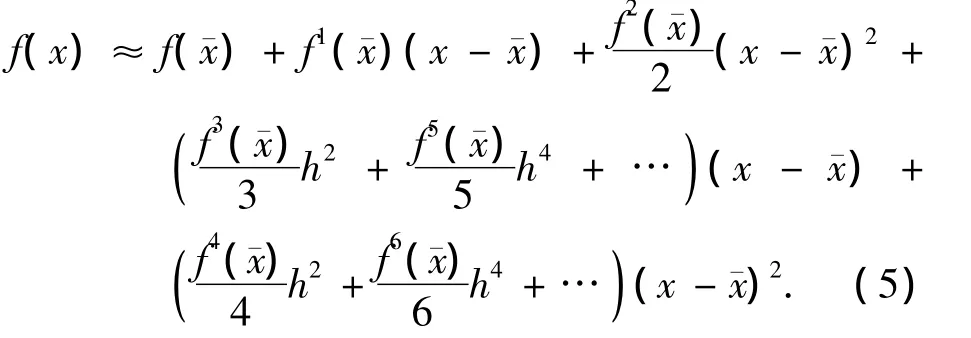
对比式(5)和对f(x)在¯x处的泰勒展开可以看出使用Stirling插值公式对非线性方程f的近似可以达到二级泰勒展开，同时选取合适的参数h还可以近似到更高级别的泰勒展开.

当表达式(1)中的输入随机变量x为多维变量时，式(2)可以重新被表示为

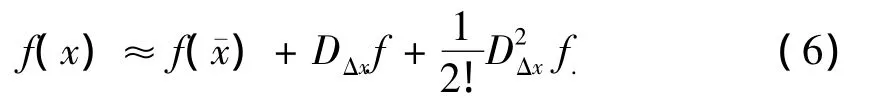
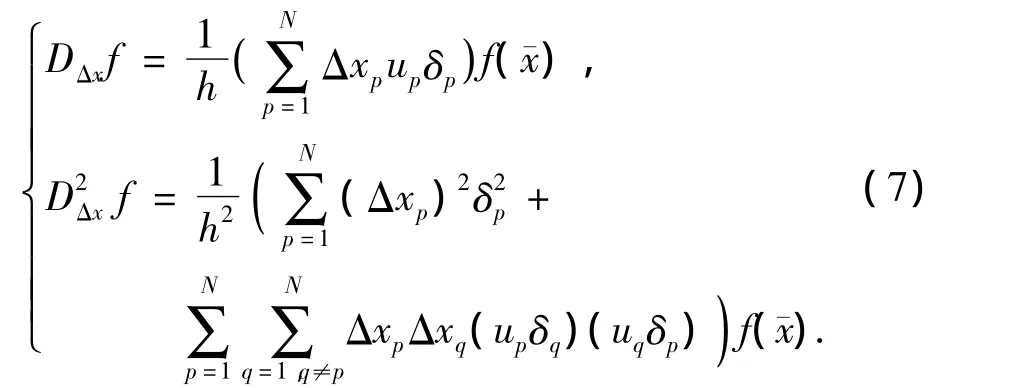
式(7)中操作符up和δp为

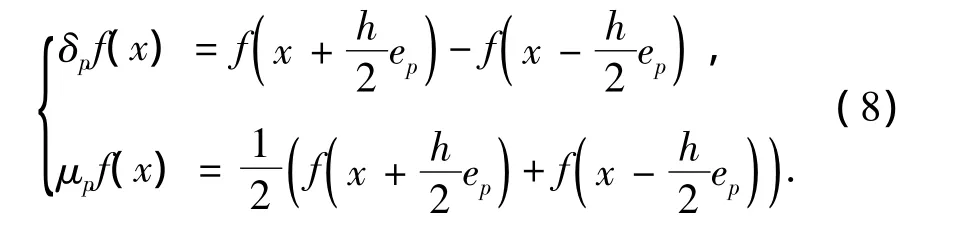
式中:ep为第p项元素为1其余项元素为0的N维向量.

式(6)中输入随机变量x经过非线性过程f后输出的均值为

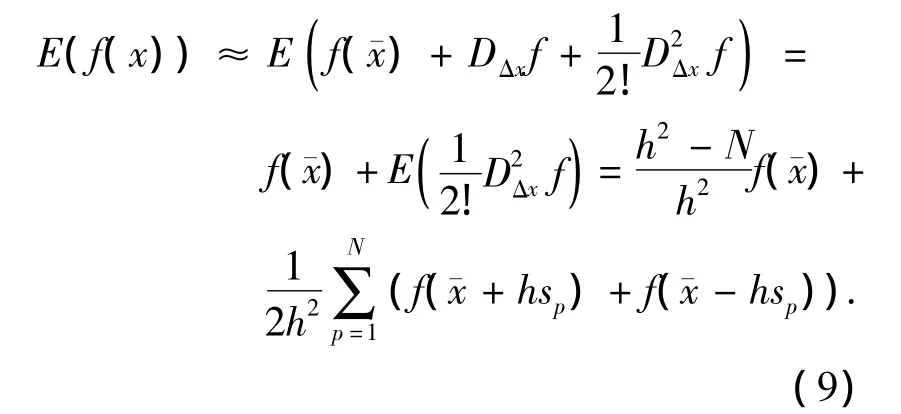
式中:sp为输入变量x的协方差Cholesky系数的第p项.

式(6)中输入随机变量x经过非线性过程f后输出的协方差以及输出和输入x之间的互协方差分别为

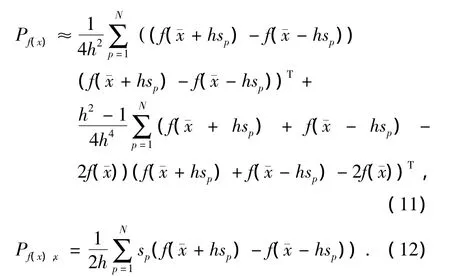
综合考虑式(9)、式(11)以及式(12)可以看出对非线性方程使用Stirling插值公式的二级展开近似后，非线性方程的输出均值、协方差以及输出和输入的互协方差完全由2N+1个输入点经过非线性方程f后的输出决定.这些输入点统称为Sigma点［12－13］.结合式(9)、式(11)和式(12)同卡尔曼滤波器组成中心差分卡尔曼滤波器，并使用此滤波器对SLAM中的状态预测方程，测量方程进行估计.

1.2 SLAM状态向量预测

在CDKFSLAM过程中，状态向量和状态向量协方差分别为

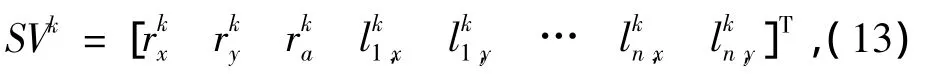
状态向量预测是指根据机器人当前状态向量SV，同时参考机器人速度和以及噪声参数预测机器人下一时刻的位置.状态向量预测方程为

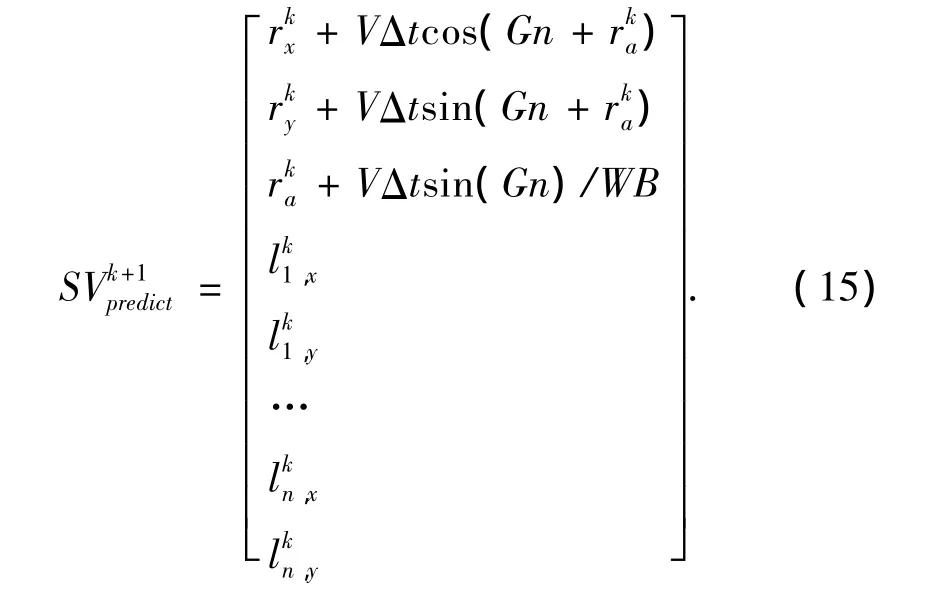
式中:V为机器人的运动速度，Δt为时刻k和时刻k+1的时间间隔，Gn为方位角噪声，WB为机器人的轮间距.

由式(15)可知为了根据k时刻的状态向量预测k+1时刻的状态向量需要使用k时刻的状态向量SVk，机器人速度参数V，机器人方位角噪声参数，时间间隔以及机器人轮间距.由于机器人速度和方位角参数受噪声影响，因此在使用Stirling多项式插值方法对式(15)进行非线性近似时对输入Sigma点的构造需要考虑机器人速度和角速度噪声.使用式(9)和式(11)对状态向量的均值和协方差预测时的输入Sigma点来进行选择

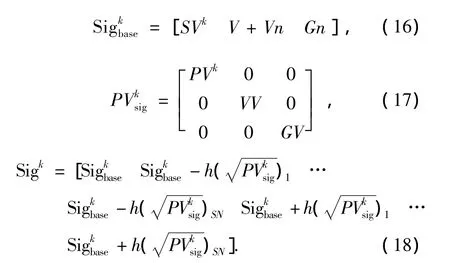
式中:V为机器人移动速度参数，Vn为机器人移动速度噪声均值，Gn为机器人方位角噪声均值，VV为机器人速度噪声协方差，GV为方位角噪声协方差.由于机器人移动速度参数和机器人方位角噪声参数的维数都为1，所以式(18)中SN=3+ 2n+1+1，输入Sigma点的总数为2SN+1，在这里机器人移动速度噪声和方位角噪声都近似认为符合高斯分布，因此参数h取值为

将式(18)中各个输入向量代入式(15)可以获得各个输入向量经过状态向量预测方程的输出，同时结合式(9)和式(11)获得预测状态向量和其协方差

1.3 SLAM状态向量更新

在机器人运动过程中接收到传感器测量数据时先根据Stirling插值方式对测量方程的输出进行估计，再使用卡尔曼滤波器对状态向量更新，测量方程为

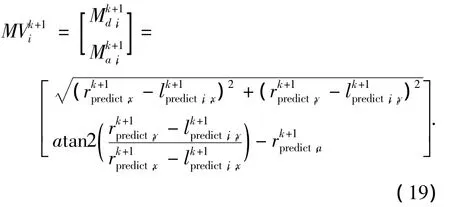
同样在使用Stirling插值方式对测量方程输出进行估计时需要考虑到测量过程的距离测量噪声和方位角测量噪声，因此此时输入Sigma点的选择为

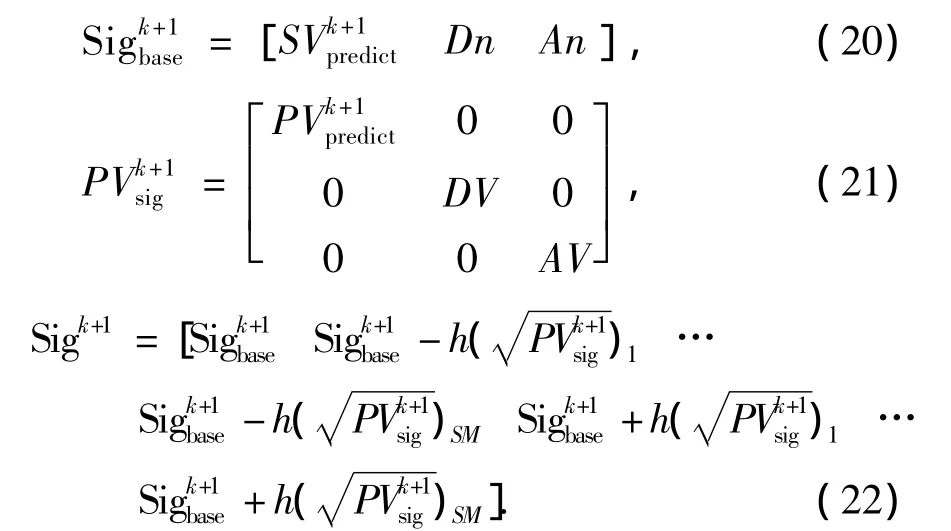
式中:Dn为距离测量噪声的均值，An为方位角测量噪声的均值，DV为距离测量噪声的协方差，AV为方位角测量噪声的协方差;由于DV和AV的维数都为1，所以式(22)中的SM=3+2n+1+1，输入Sigma点总数为2SM+1，参数h取值为

在测量数据过程中，由于距离测量噪声和方位角测量噪声与状态向量SV互不相关并且测量式(19)的输出即为机器人和路标之间的相对距离和相对方位角，所以对测量方程的输入Sigma点的选取可以简化为

同时对均值和协方差的估计需要由式(9)、式(11)修正为

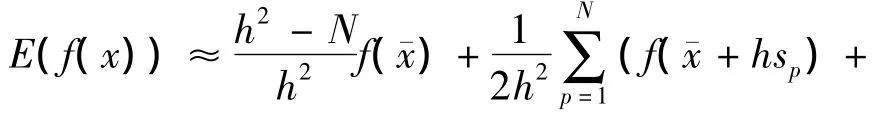
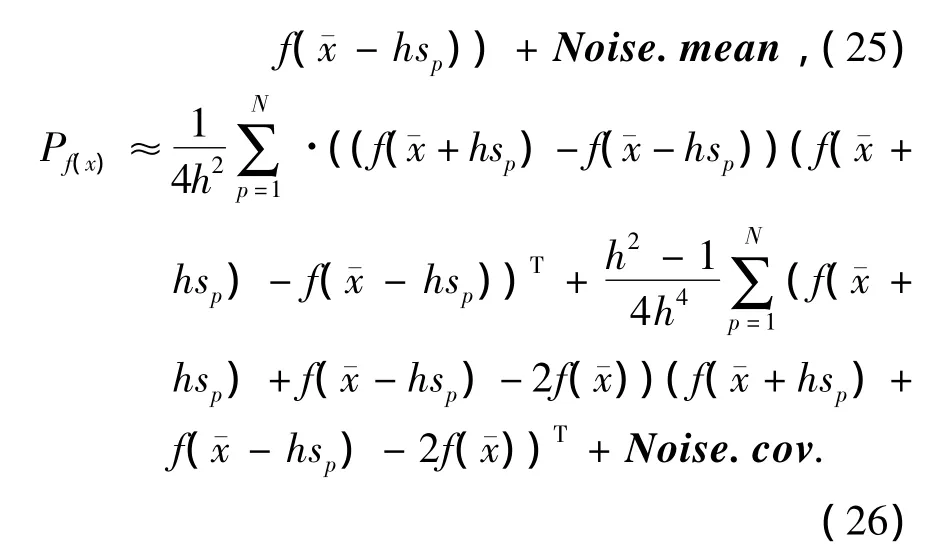
式中:Noise.mean为噪声均值所组成的向量，Noise.cov为噪声协方差所组成的协方差矩阵.从式(25)和式(26)可以看出此时噪声参数对于非线性输出的估计可以认为是单纯的附加量.

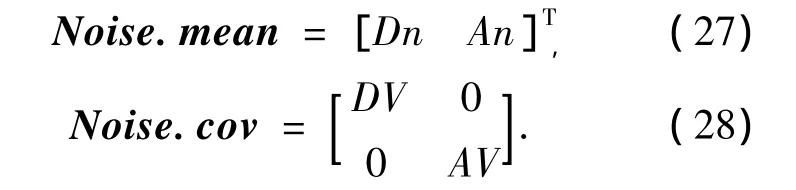
相对于使用式(20)～式(22)对测量方程输出的估计使用式(23)～式(28)时输入Sigma点数目从2(3+2n+1+1)+1降低为2(3+2n)+ 1，从而降低了时间占用量.当使用式(23)～式(28)获得对第i个路标的测量数据向量MVk+1和测量数据向量协方差矩阵 PMVk+1后，根据式(12)获取测量方程的输入变量和测量方程输出MVk+1的协方差为

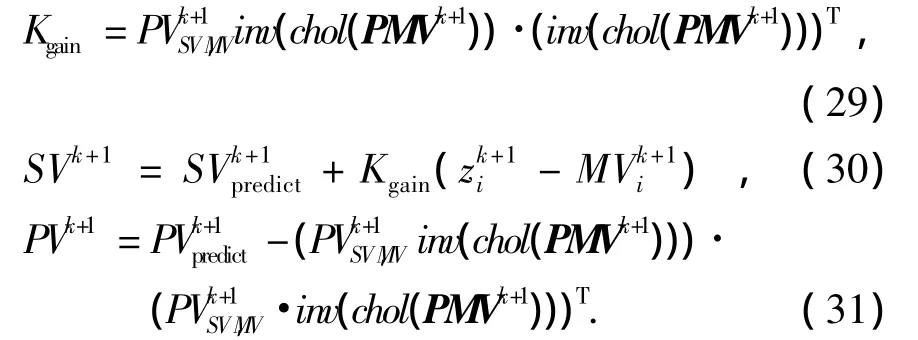
1.4 状态向量及状态协方差动态调整

由状态向量和状态向量协方差矩阵可知随着已检测到路标数目的增大状态向量SV和状态向量协方差PV的维数都会逐渐增大，这样会严重影响SLAM的速度.因此根据已测量到的路标统计信息提出一种动态状态向量和状态向量协方差调整的方法.假设k时刻之前所检测到的路标索引序列为

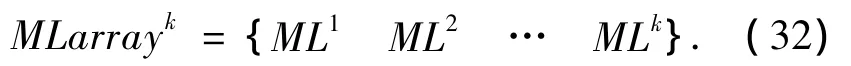
式中:MLi为在第i时刻所检测到的路标索引序列.根据检测路标统计信息计算每个路标对于当前时刻状态向量的影响权重，同时依据此权重对当前状态向量和状态向量协方差实现动态调整.

为简单起见，在k时刻计算各个路标权重时只考虑到k之前的m个时刻的路标统计信息，m取值范围为1～k，距离当前时刻k越近的路标索引序列所对应的权重系数越大.这样k时刻所参考的路标索引序列为

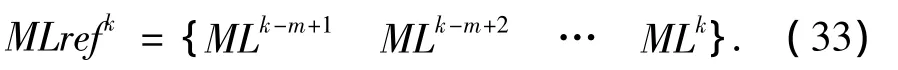
每次路标索引的权重系数满足wk＞wk－1＞… ＞wk－m+2＞wk－m+1，权重系数为

在时刻k各个路标的权重为

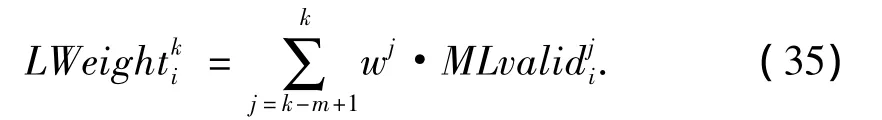
式中:i为路标索引.

式中:当路标i包括在检测路标索引序列MLj中时其值为1，否则为0.

为将状态向量SV和状态向量协方差矩阵PV控制在固定大小内，定义阈值MAXLM，MAXLM为在SV和PV中所包含的最大路标数.当SV和PV中路标数目大于MAXLM时首先通过式(35)获取每个路标在此时刻的权重，然后在SV和PV中找到权重最小的路标并将其从SV和PV中删除，直至SV和PV中所包含路标数目小于等于MAXLM.当在后续时刻重新检测到被删除过的路标时将其作为未被检测过的路标对待.

1.5 初始状态及其协方差确定

由于在初始状态时还未检测到任何路标，因此初始状态向量SV1和状态向量协方差PV1中只包括机器人位置信息.

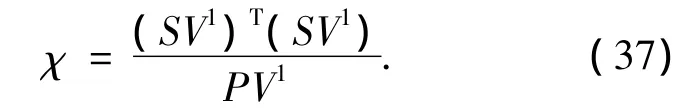
SV1和PV1组成的式(37)满足自由度为3的卡方分布，根据一致性理论［14］可知当式(37)的值位于双边概率为95%的区域时认为其符合一致性要求.由卡方分布可知此时双边概率区域为［0.22 9.35］.

根据上述要求，当速度噪声满足N～(0，VV)，方位角噪声满足N～(0，AV)时，初始状态向量和状态向量协方差取值为

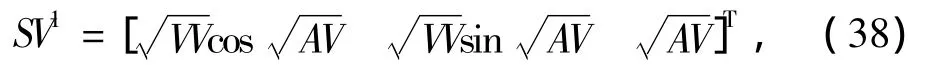
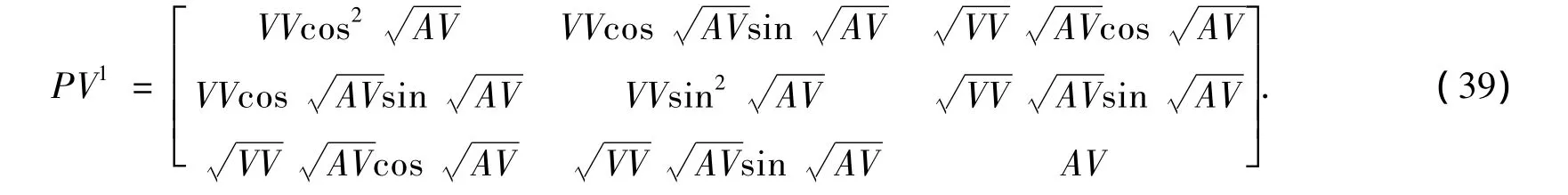
此时式(38)和式(39)满足一致性要求.

2 内存分析

在CDKFSLAM算法中所占用的内存由状态向量SV，状态向量协方差PV以及参考路标序列MLref组成.当环境中路标总体数目为LN时，CDKFSLAM占用的最大内存为

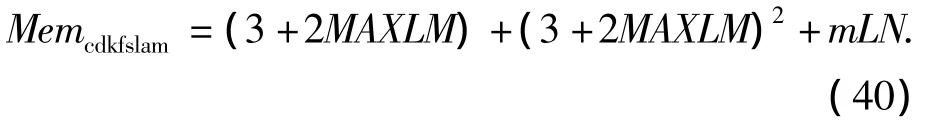
式中:(3+2MAXLM)为状态向量SV大小，(3+ 2MAXLM)2为状态向量协方差PV大小，mLN为参考路标序列大小.

EKFSLAM算法中内存占用量由状态向量和状态向量协方差组成，其占用最大内存为

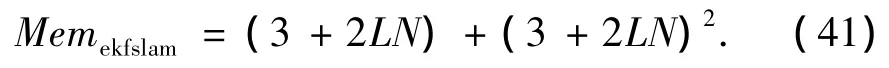
在FASTSLAM中，内存占用量和粒子数目有关.每个粒子所占用内存由机器人位置向量，机器人位置协方差，各个路标位置向量以及各个路标位置协方差组成.假设粒子数目为PMAX，其占用最大内存为

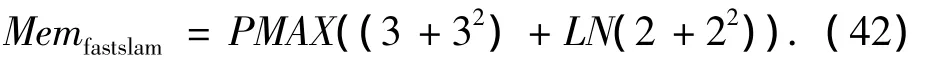
式中:(3+32)为机器人位置向量和位置向量协方差大小，(2+22)为每个路标位置向量和位置向量协方差大小.

对比式(40)～式(42)可知CDKFSLAM和FASTSLAM的内存占用和环境中路标总数LN成线性关系，EKFSLAM的内存占用和LN成二次型关系.图1描述了 CDKFSLAM、EKFSLAM和FASTSLAM的内存占用情况随路标数目LN变化的关系，其中，m取值为10.从图1中可以看出CDKFSLAM对内存的占用要少于EKFSLAM和FASTSLAM.

3 实验

本实验在稀疏路标环境和密集路标环境下使用CDKFSLAM和FASTSLAM2.0分别进行测试.稀疏路标环境大小为250 m×200 m，包含35个路标;密集路标环境大小为250 m×200 m，包含135个路标.移动机器人轮间距为4 m，所使用传感器最大检测距离为30 m，检测角度范围为0～180°.SLAM过程中状态向量预测的频率为400 Hz，测量数据的获取频率为50 Hz.机器人运动过程中速度噪声方差为0.3 m，方位角噪声方差为3°;传感器测量过程中测量距离噪声方差为0.1 m，角度方差为1°.CDKFSLAM中状态向量中的最大路标数目MAXLM为10，权重计算时所参考的路标序列数目m=10，FASTSLAM2.0中粒子数目取PMAX=10.

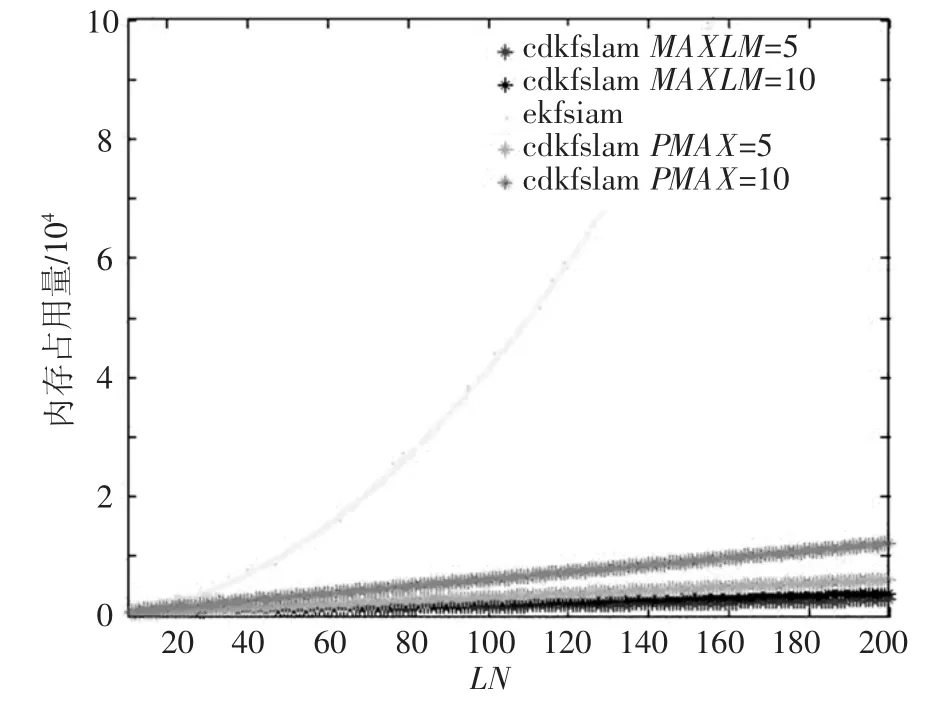
图1 CDKFSLAM、EKFSLAM和FASTSLAM内存比较

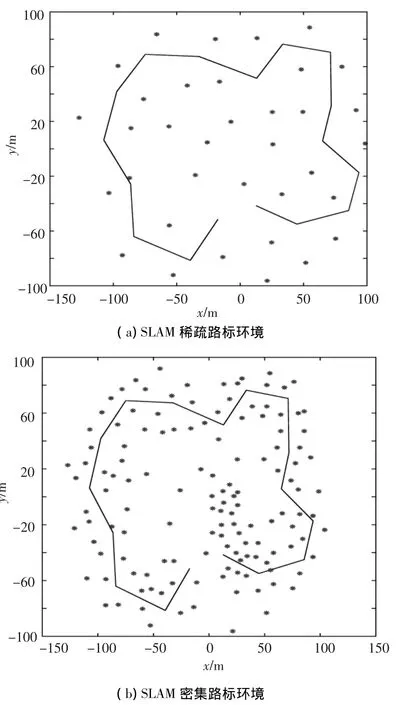
图2 稀疏路标环境下和密集路标环境下SLAM的比较

在稀疏路标环境下使用 CDKFSLAM和FASTSLAM2.0分别进行45次实验.图3中为每次MMSE(Minimum Mean Square Error)比较.图4为CDKFSLAM和FASTSLAM2.0在不同时刻时状态向量预测和状态向量更新所消耗的时间.从图4中可以看出，FASTSLAM2.0所消耗的时间要大于CDKFSLAM.

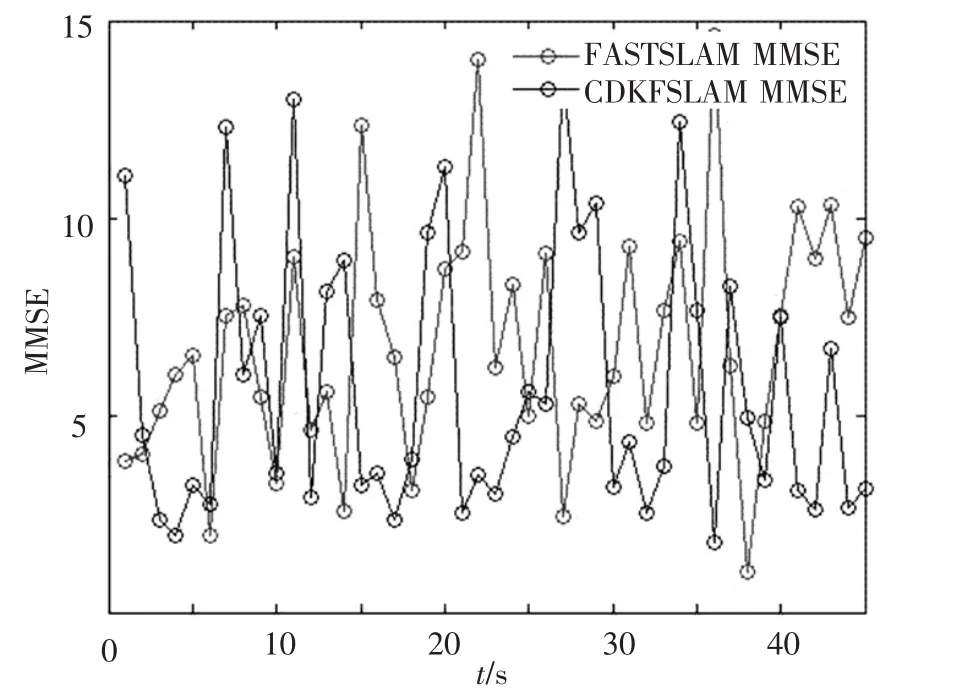
图3 稀疏路标环境下CDKFSLAM和FASTSLAM的MMSE比较

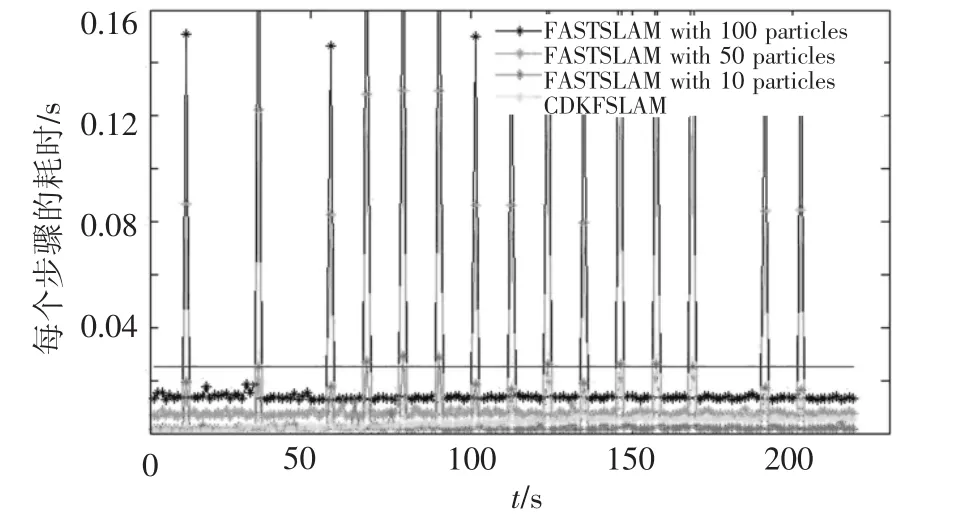
图4 稀疏路标环境下CDKFSLAM和FASTSLAM的消耗时间比较

在密集路标环境下，图5中为每次MMSE (Minimum Mean Square Error)比较.图6为CDKFSLAM和FASTSLAM2.0在不同时刻状态向量预测和状态向量更新所消耗的时间.从图6中可以看出FASTSLAM所消耗的时间要大于CDKFSLAM，与稀疏环境相比，CDKFSLAM所消耗的时间增大，这是因为在密集环境下动态调整状态向量SV和PV的频率加大的缘故.

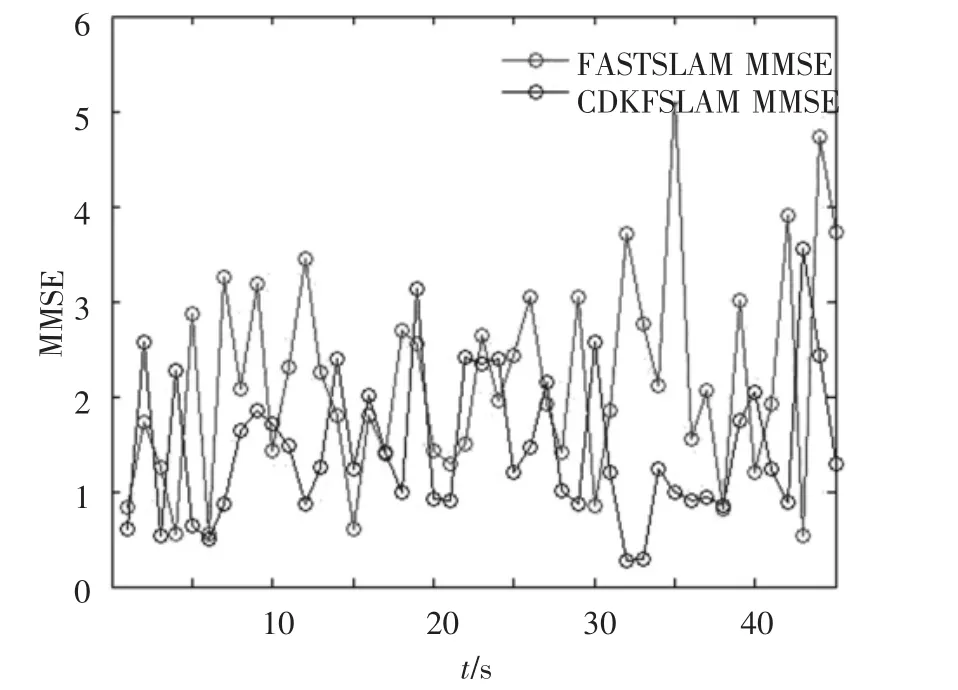
图5 密集路标环境下CDKFSLAM和FASTSLAM的MMSE比较

4 一致性分析

使用 NEES(NormalizedEstimationError Squared)作为对移动机器人SLAM过程中定位结果的一致性分析依据，NEES定义为

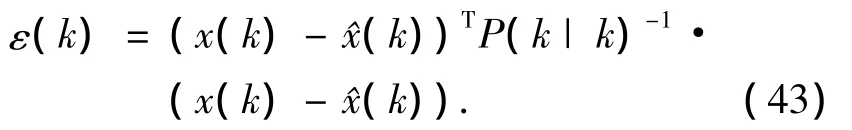
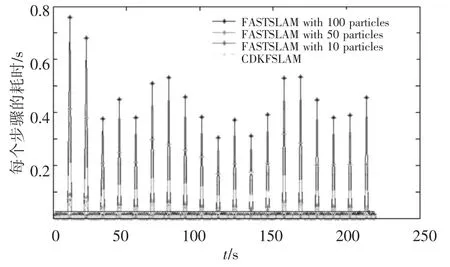
图6 密集路标环境下CDKFSLAM和FASTSLAM的消耗时间比较

对CDKFSLAM和FASTSLAM2.0分别进行45次实验，使用45次的平均NEES作为一致性分析依据.由卡方分布属性可知符合自由度为45×3的卡方分布，当考虑双边概率为95%的区域作为一致性区域时可得位于此区域内时表示当前机器人位置估计满足一致性要求，否则表示机器人位置估计不满足一致性要求.图7(a)为稀疏路标环境下通过45次实验所得的CDKFSLAM的一致性数据，图7(b)为粒子数为10时FASTSLAM2.0的一致性数据.图8(a)为密集路标环境下CDKFSLAM的一致性数据，图8(b)为粒子数为10时FASTSLAM2.0的一致性数据.的双边区域为［2.32 3.75］，当

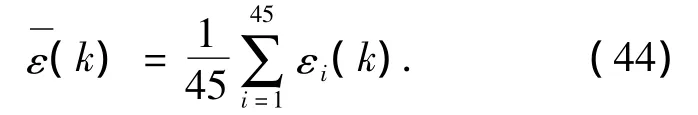
表1是对图7和图8中位于一致性区间内点数的统计，比较可以看出无论是在稀疏路标环境下还是在密集路标环境下使用CDKFSLAM所得的机器人位置一致性都要优于粒子数目为10的FASTSLAM2.0.对比图3和图5可以看出对CDKFSLAM而言在密集路标环境下的MMSE均值要优于稀疏路标环境下的结果，但从一致性结果(图7，图8和表1)上来看却恰恰相反，在稀疏环境下CDKFSLAM的一致性要优于密集环境下的结果.这是由于在MMSE计算过程中并没有考虑协方差矩阵，由此可以看出在对SLAM结果的分析过程中使用一致性分析要比使用MMSE更加合理.

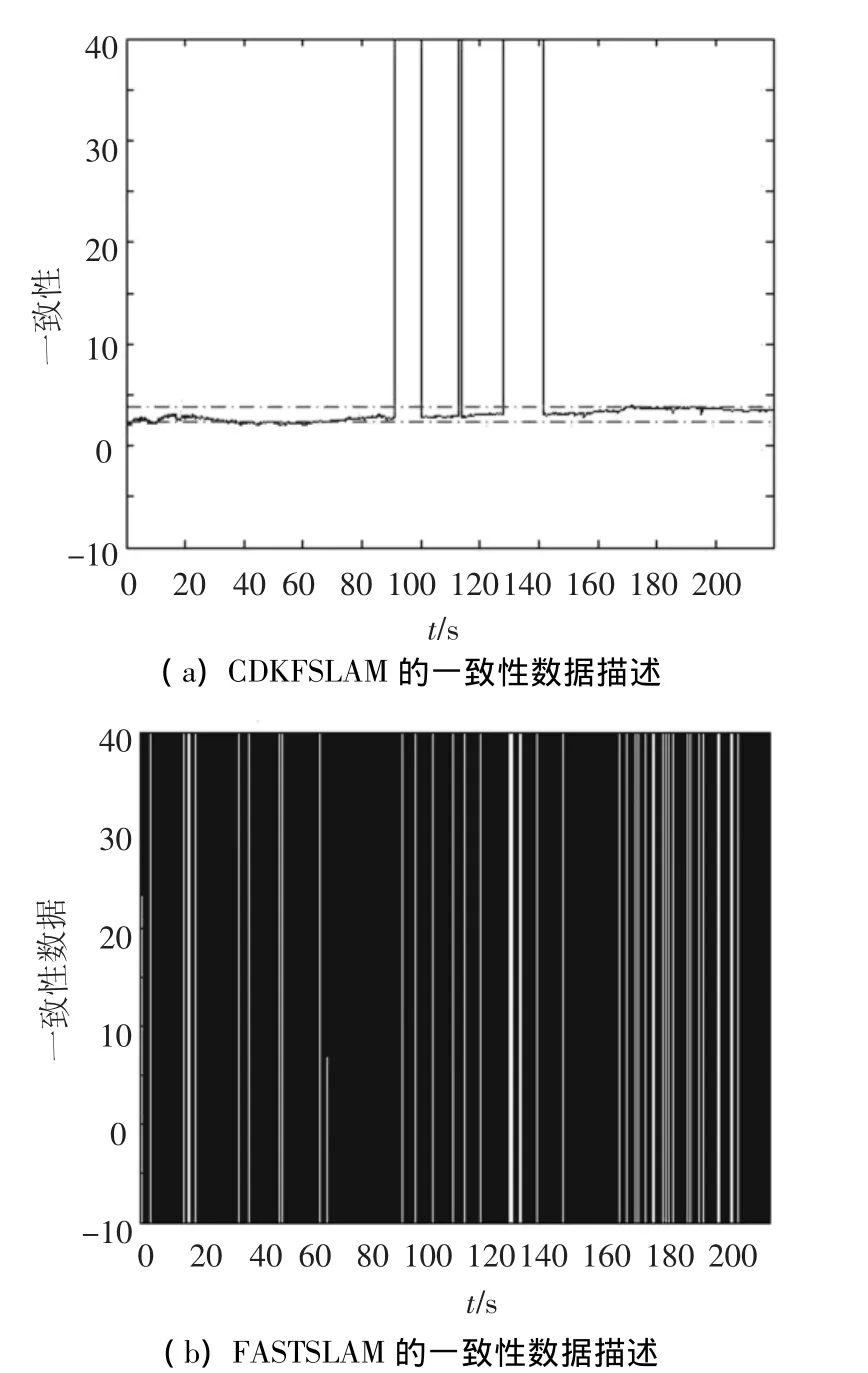
图7 稀疏路标环境下使用CDKFSLAM和FASTSLAM所得机器人位置一致性

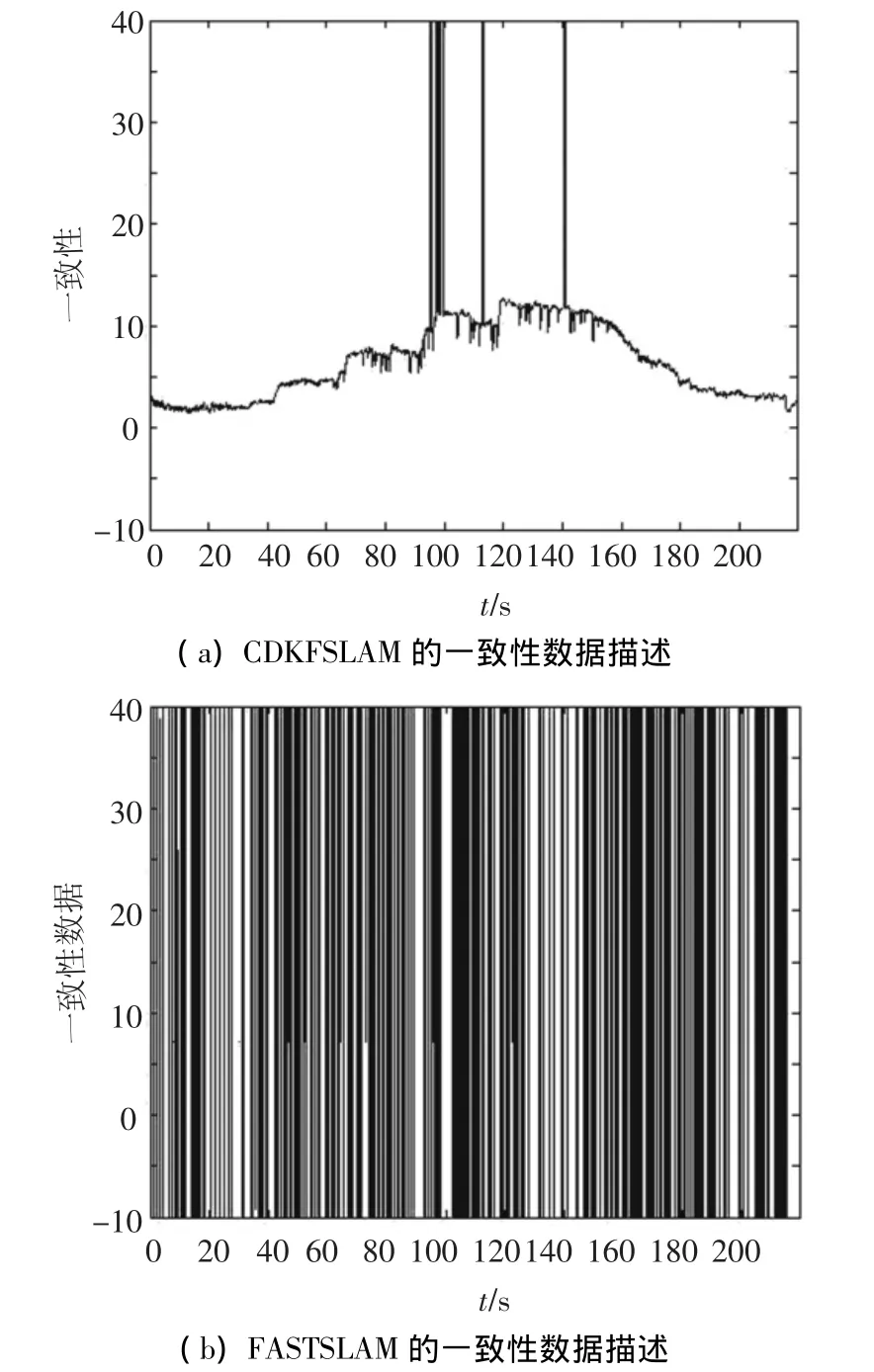
图8 密集路标环境下使用CDKFSLAM和FASTSLAM所得机器人位置一致性

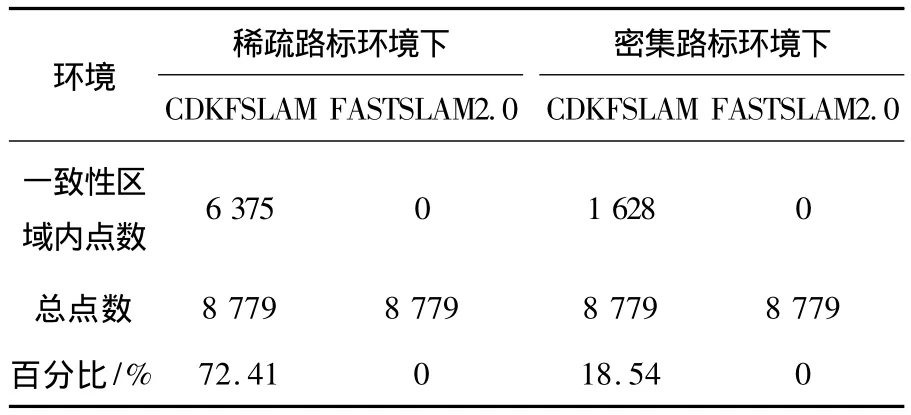
表1 CDKFSLAM和FASTSLAM一致性分析

5 结论

1)选取合适的参数时使用Striling多项式插值方法对非线性近似可以达到二级甚至更高级的近似，从而提高了SLAM结果的一致性.

2)使用已经测量到的路标统计信息估计各个路标对当前状态向量的影响权重，使用各个路标权重动态调整状态向量和状态协方差将其控制在固定大小内虽然在一定程度上丢失了一些历史信息，但可以使其在密集型路标环境下达到较快的SLAM速度从而可以提高实际应用的可行性.

3)从实验结果可以看出本文算法的SLAM MMSE结果要优于FASTSLAM，从一致性分析中可以看出在稀疏环境和密集环境下CDKFSLAM的一致性都优于粒子数目为10的FASTSLAM;另外从一致性结果和MMSE比较可以看出对SLAM结果的评价时使用一致性评价要比使用MMSE更加合理.

［1］SMITH R，SELF M，CHESSEMAN P.Estimating uncertain spatial relationships in robots［C］//Autonomous Robot Vehicles.New York，NY:Springer-Verlag New York，Inc，1990:167－193.

［2］DURRANT-WHYTE H，BAILEY T.Simultaneous localization and mapping:Part I［J］.IEEE Robotics and Automation Magazine，2006，13(2):99－110.

［3］BAILEY T，DURRANT-WHYTE H.Simultaneous localization and mapping:Part II［J］.IEEE Robotics and Automation Magazine，2006，13(3):108－117.

［4］KIM C，SAKTHIVEL R，CHUNG W K.Unscented FastSLAM:A robust and efficient solution to the slam problem［J］.IEEE Transactions on Robotics，2008，24(4):808－820.

［5］BAILEY T，NIETO J，NEBOT E.Consistency of the FastSLAM algorithm［C］//Proceeding of IEEE International Conference on Robotics and Automation.Orlando，FL:IEEE，2006:424－429.

［6］MONTEMERLO M，THRUN S，KOLLER D，et al.FastSLAM 2.0:An improved particle filtering algorithm for simultaneous localization and mapping that provably converges［C］//Proceeding of the International Conference on Artificial Intelligence.Acapulco，Mexico: Springer，2003:1151－1156.

［7］THRUN S，KOLLER D，GHAHRAMANI Z，et al.Simultaneous Mapping and Localization with Sparse Extended Information Fulters:Theory and Initial Results［R］.［S.l.］:CMU，2002.

［8］THRUN S，LIU Y F，KOLLER D，et al.Simultaneous mapping and localization with sparse extended information filters［J］.The International Journal of Robotics Research，2004，23(7/8):693－716.

［9］WAN E A，Van der MERWE R.The unscented kalman filter for nonlinear estimation［C］//Proceedings of A-daptive Systems for Signal Processing，Communications and Control Symposium.Lake Louise，Alta:IEEE，2000:153－158.

［10］NORGAARD M，POULSEN N，RAVN O.New developments in state estimation for nonlinear systems［J］.Automatica，2000，36(11):1627－1638.

［11］NORGAARD M，POULSEN N，RAVN O.Advances in Derivative-Free State Estimation for Nonlinear Systems［R］.［S.l.］:Denmark，2004.

［12］Van der MERWE R.Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models［D］.Oregon:Oregon Health＆Science University，2004.

［13］WANG X，ZHANG H.A UPF-UKF framework for SLAM［C］//Proceedings of International Conference on Robotics and Automation.Roma:IEEE，2007:1664－1669.

［14］BAR-SHALOM Y，RONG L X，KIRUBARAJAN T.Estimation with Applications To Tracking and Navigation［M］.New York，NY:Wiley-Interscience Publication，2001.