TS模型和H∞观测器在卫星故障诊断中的应用

王宇雷，李传江，马广富

(哈尔滨工业大学控制科学与工程系，哈尔滨150001，hit－raynking@yahoo.cn)

随着新一代卫星技术的发展，对卫星姿态控制系统的可靠性和自主运行能力的要求都有了很大的提高，其中自主故障诊断技术是其它自主运行技术的基础.因此，研究卫星姿态控制系统的智能故障诊断技术具有重要意义.

按照Frank P M［1］的观点，目前比较成熟的故障诊断方法大致可分为三类:基于信号处理的方法、基于模型的方法和基于知识的方法.其中，基于模型的方法以系统的数学模型为基础，利用观测器构建残差，进行故障评价和决策.它的优点在于利用解析冗余取代硬件冗余;可以诊断出未知故障，不需要历史的经验知识.

近30年来，国内外许多学者提出了多种基于模型的故障诊断方法:文献［2－3］基于自适应技术构建残差诊断和分离传感器故障.文献［4－5］基于H∞最优控制思想，将故障诊断问题转化为标准H∞最优控制器设计问题.与此同时，鲁棒故障诊断［6－7］，复杂系统故障诊断［8］和条件非线性故障诊断［9］相继提出，不断扩展和丰富故障诊断的概念.

但是，上述故障诊断方法大多针对线性系统.由于缺乏处理非线性问题的统一方法，具有强耦合非线性特性的卫星姿态系统故障诊断问题仍然有待进一步研究.文献［10］首先提出了TS模糊方法，该方法利用模糊规则近似逼近非线性系统.因此，可以用来解决许多非线性故障观测器设计和控制设计问题，同样该方法也适用于卫星姿态控制系统［11］.

本文基于TS模糊模型，设计H∞最优故障观测器，构建残差信号，研究姿态控制系统陀螺故障问题.受文献［12］启发，考虑两种TS模糊模型:先验变量已知和先验变量未知.针对TS模糊模型中的局部线性系统分别设计H∞最优故障观测器，使得故障信号到状态估计误差的无穷范数最小，并基于并行分布补偿(PDC)原则给出了基于TS模型的H∞最优故障观测器的设计方法.

1 预备知识

1.1 卫星姿态动力学

刚体卫星的动力学方程［13］为

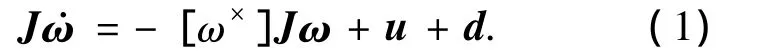
其中:ω=［ω1ω2ω3］T∈R3表示为卫星本体系相对于惯性系且投影在本体系上的姿态角速度.J∈R3×3为卫星的对称正定转动惯量矩阵; u=［u1u2u3］T∈R3表示为三轴控制力矩; d=［d1d2d3］T∈R3为卫星在轨飞行时的干扰力矩.定义

定义状态变量x=ω并且考虑陀螺故障fs，式(1)可以重写为如下形式:

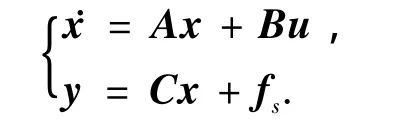
其中:

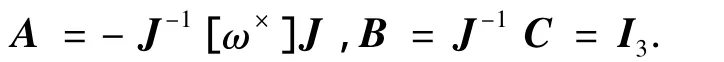
1.2 TS模糊模型

TS模糊系统模型利用一系列IF－THEN模糊规则近似逼近非线性系统.其中每条规则表征系统一个局部线性化模型.本文考虑一类连续TS模糊系统模型描述如下:

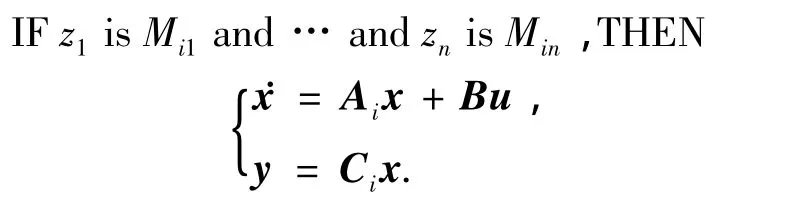
其中:i=1，2，…，r;z1，z2，…，zn代表先验知识，这里定义为系统的状态变量，Mij为隶属函数，r为模糊规则数.假设系统状态变量和控制输入已知，考虑传感器故障，最终整个系统的状态方程可以写为

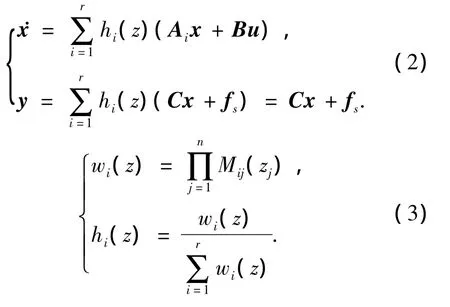
其中:

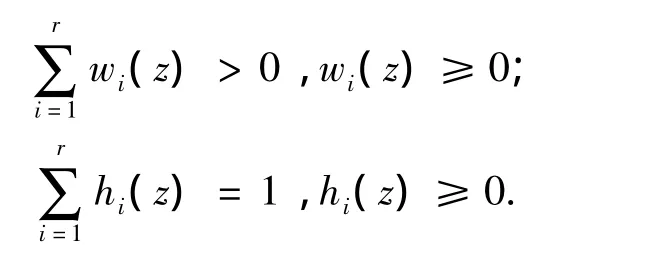
对于给定的TS模糊模型，基于PDC原则给出了模糊观测器的设计方法如下:

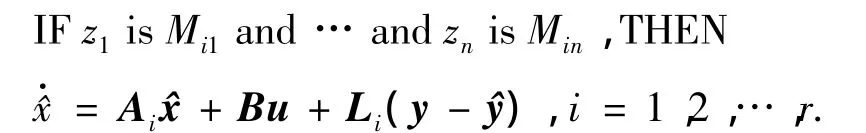
式中:Li∈R3×3为第i子系统的动态反馈增益.可得全局TS模糊观测器为

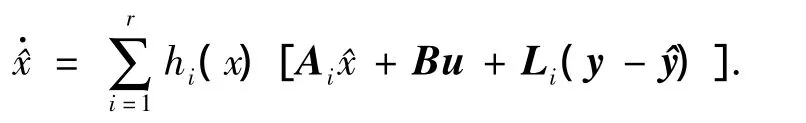
2 H∞最优故障观测器设计

应用H∞鲁棒控制思想［5，9］设计基于TS模糊模型的H∞最优故障观测器，分为以下两种情况:

情况A:先验知识z已知，令z=x;

2.1 情况A:H∞最优故障观测器设计

基于PDC原则，设计全局H∞最优故障观测器如下:

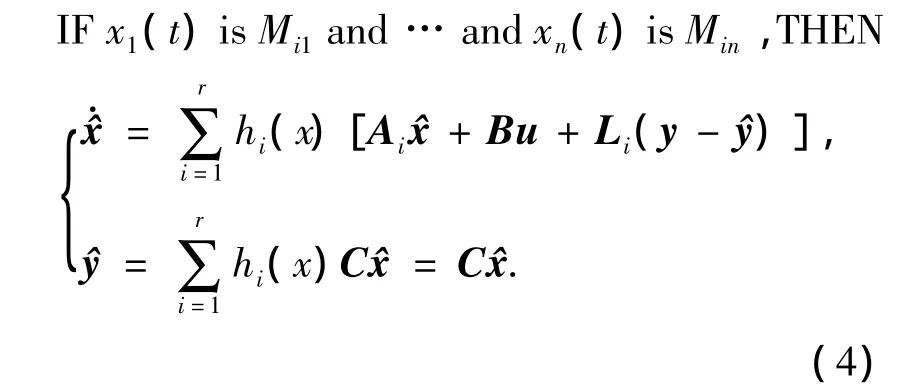
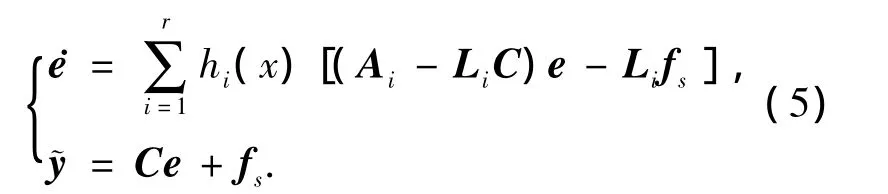
通过设计H∞最优故障观测器使得状态观测误差e达到最小，从而使得输出误差直接跟踪陀螺故障信号.根据鲁棒控制理论，式(5)可以转换为H∞标准结构

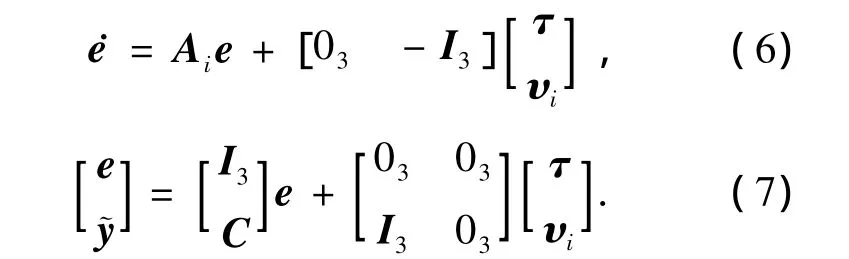
其中:

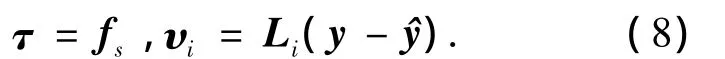
通过式(6)～(8)，将传感器故障问题转换为H∞控制器求解问题，那么利用已有的鲁棒控制理论可以方便地解决此问题，有关H∞控制器的实现和求解方法参见文献［14］.

考虑陀螺故障，权重函数可以选择为ωl(s)= b/(s+c)，这里参数b的选取决定考察对象的带宽，参数c是为了满足H∞方程可解条件［15］，一般设置为小量.那么得到增广的广义传递函数为

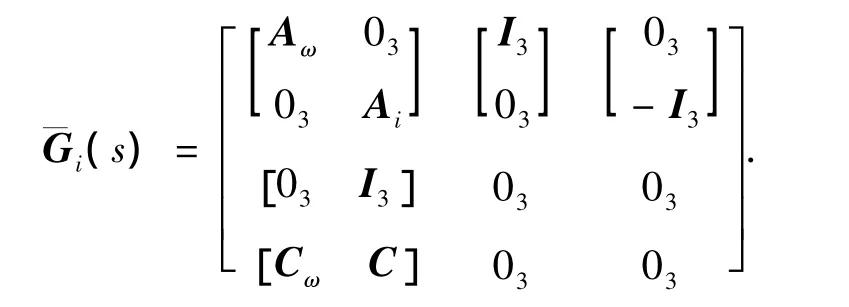
其中:Aω=diag(－c，－c，－c)，Cω=diag(b，b，b)分别表示以－c和b为对角元素的对角矩阵.综上所述，可以得出设计H∞最优故障观测器的定理(证明参见文献［14］).

2.2 情况B:H∞最优故障观测器设计

当实际系统发生陀螺故障时，系统的真实状态x不能通过测量直接获取，即先验知识z未知.这使得观测器的设计变得更为复杂.不同于A情况，使用观测值作为系统的先验知识z，仍然依据并行分布补偿原则，设计全局H∞最优故障观测器如下:

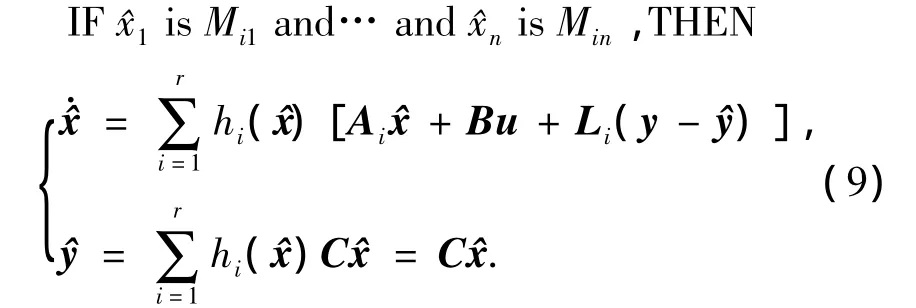
与情况A相似，由式(2)，(8)和(9)可以得到误差状态方程为

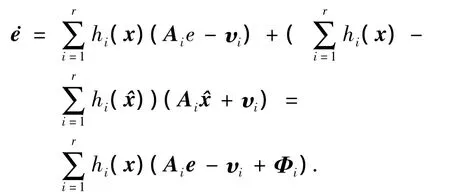
其中:

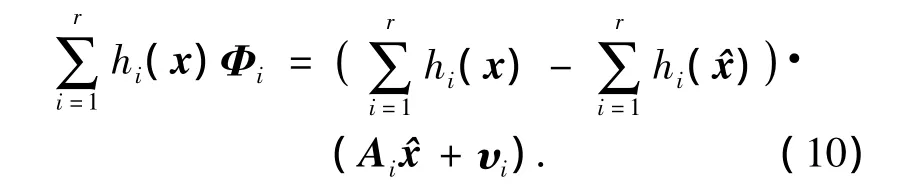
如不特殊说明，文中‖A‖均指矩阵A的2－范数.定义如下假设:

假设1 系统状态在有限观测时间内2－范数有界，即

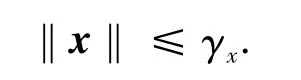
假设2 陀螺故障在有限观测时间内2－范数有界，即

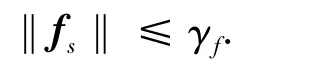
假设3 动态H∞鲁棒控制器Li(s)和系统状态矩阵Ai在有限观测时间内2－范数有界，即

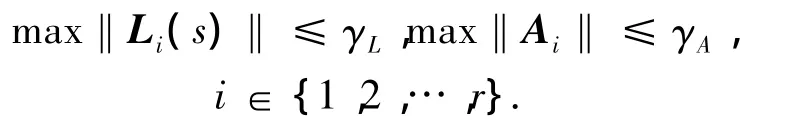
假设4 存在正实数k＞0使得hi(x)满足局部Lipschitz条件

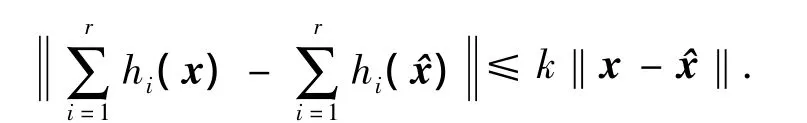
根据上述假设，由式(10)得到

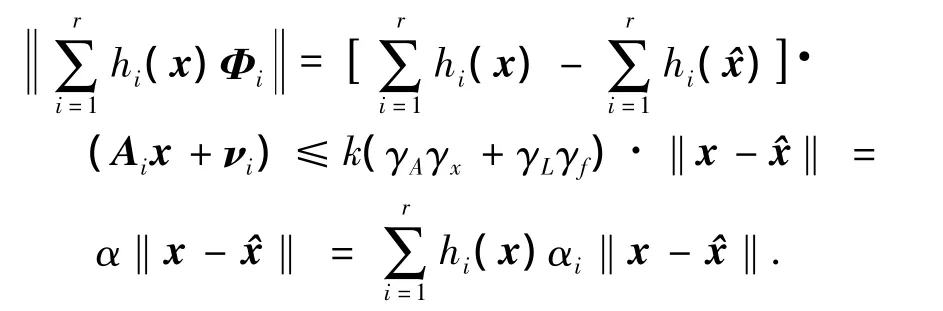
其中:

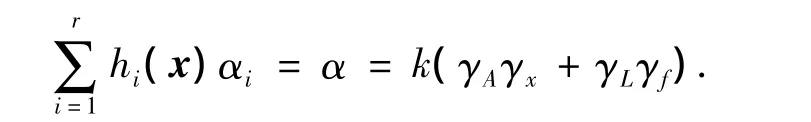
由式(3)得hi(x)总和为1，令所有αi均等于α，表示某一给定正数.那么TS模糊模型中每个Φi均满足如下局部Lipschitz条件:

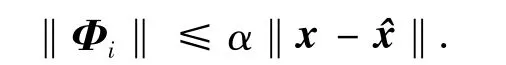
上述的假设和推导将TS模糊模型不确定的先验知识转换为系统模型未知摄动，这样便可利用已有知识解决该问题.

引理［9］如果存在观测器增益L(s)使得对具有Lipschitz不确定性Φ的被观测系统的估计误差渐近稳定，那么闭环系统传递函数满足

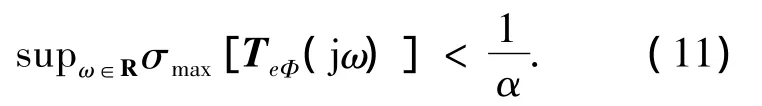
由上述引理可知，式(11)保证了观测器具有鲁棒稳定性，将陀螺故障对观测器的影响分为“直接作用”fs和“间接作用”Φi(x，fs).如图1所示，在设计H∞最优故障观测器时必须同时考虑上述两种作用的共同影响.

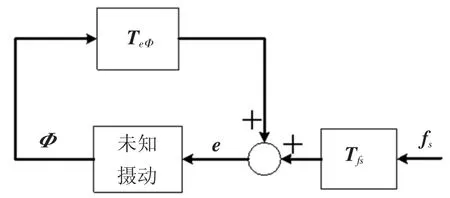
图1 直接作用和间接作用相互关联

沿用式(4)的观测器结构，情况B的误差状态方程可以写为

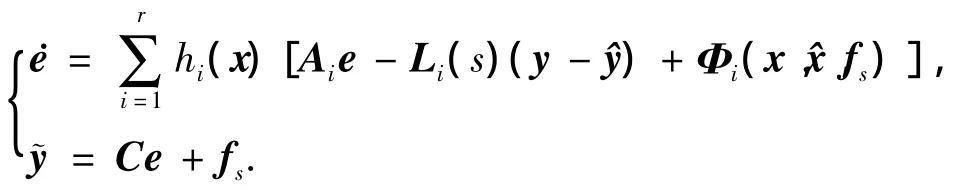
针对每个局部观测器定义

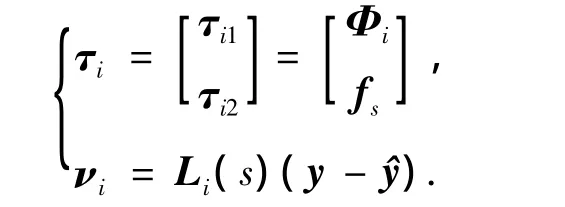
于是，情况B的H∞标准结构可以写为

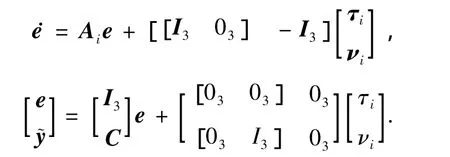
综上所述，可以得出设计情况B的H∞最优故障观测器的定理如下:

由定理2可得，TS模型H∞故障观测器设计问题实际上等价于多评价H∞控制器设计问题，为使多评价输出条件相容，构造常数ε＞0和加权函数W(s)使得

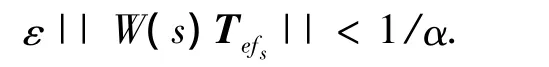
这样，情况B的H∞标准结构如图2所示.

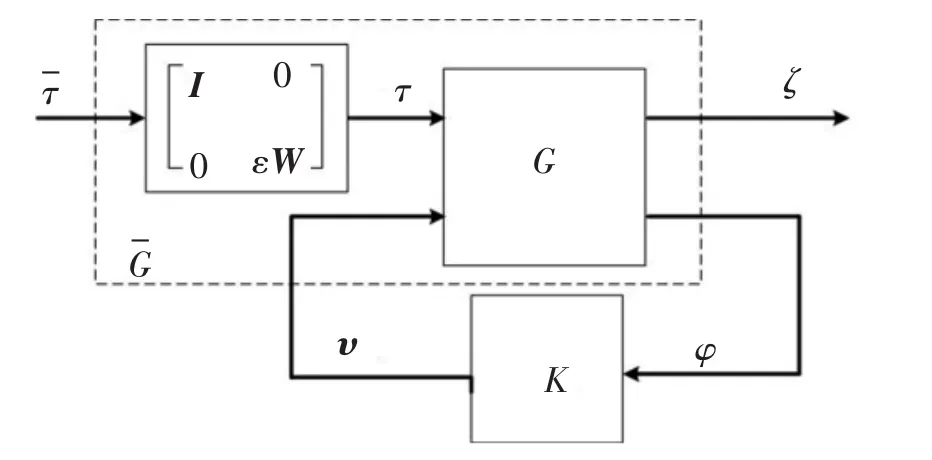
图2 增广H∞标准结构

广义被控对象写为

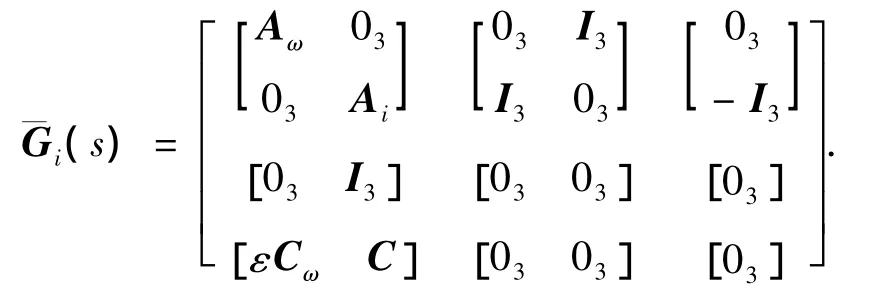
其中:

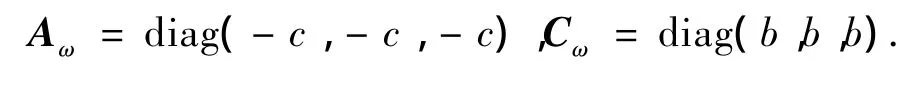
3 仿真结果

本节在MATLAB/Simulink环境下对卫星陀螺故障进行仿真研究，验证H∞最优故障观测器的有效性.卫星动力学模型由式(1)表示，选飞轮为执行机构，假定故障发生后的飞轮以最大力矩0.15 N·m输出.以光纤陀螺作为姿态角传感器.表1列出了光纤陀螺常见的两类故障.

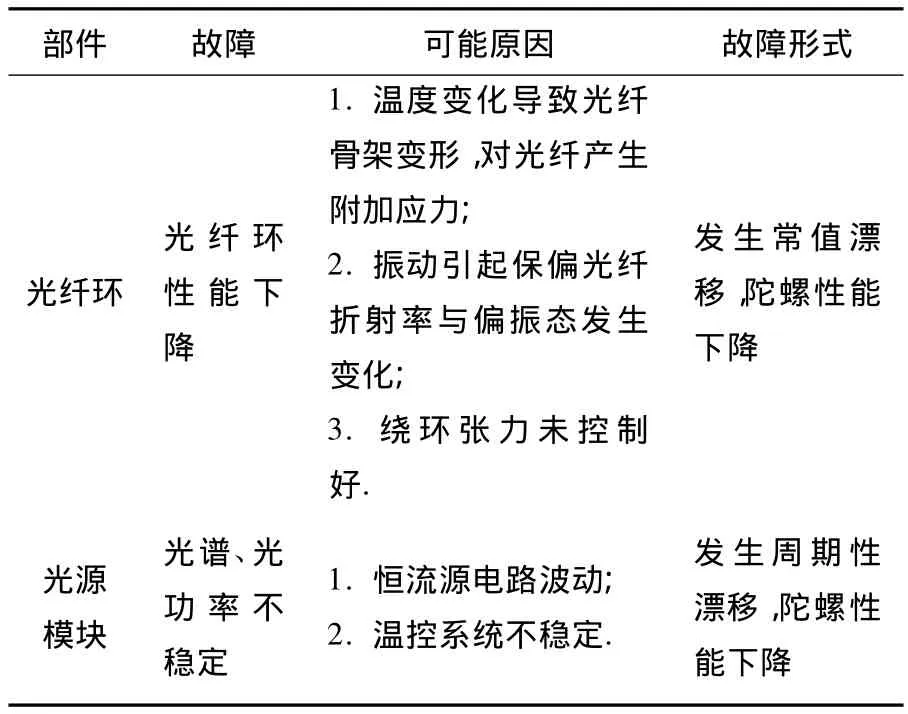
表1 光纤陀螺常见故障

根据表1中的实际故障，本文分别在以下两种故障情况下进行仿真.

故障一:假定三轴陀螺在10 s时均发生常值漂移，大小为0.1 rad/s.

故障二:假定三轴陀螺在10 s时均发生周期性漂移，大小为0.05 sin(0.5t)rad/s.

为了减少TS模型H∞故障观测器设计的复杂性，需要尽量采用较少的规则，本文选择以下9个工作点:

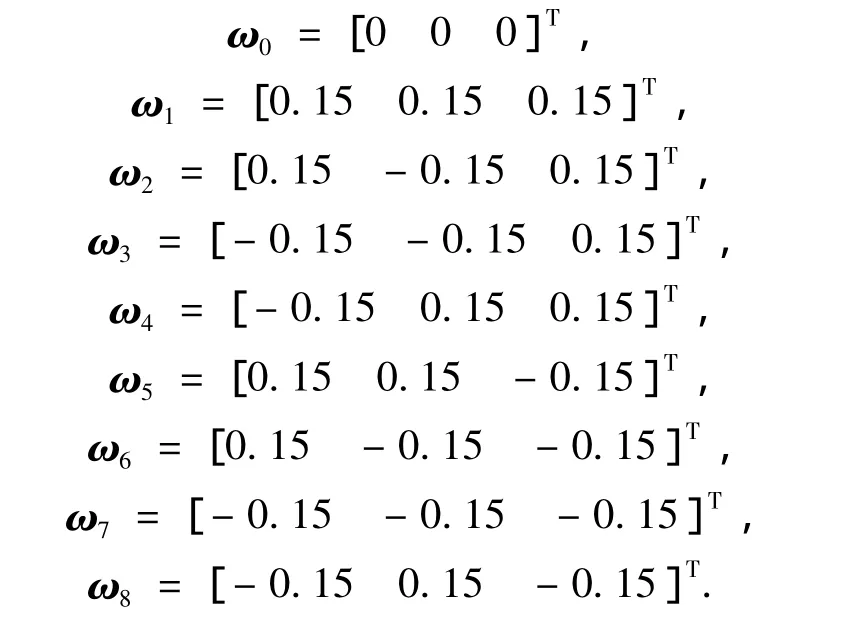
隶属函数Mij规则如图3所示.

权重函数参数b=20，c=0.001.卫星转动惯量为

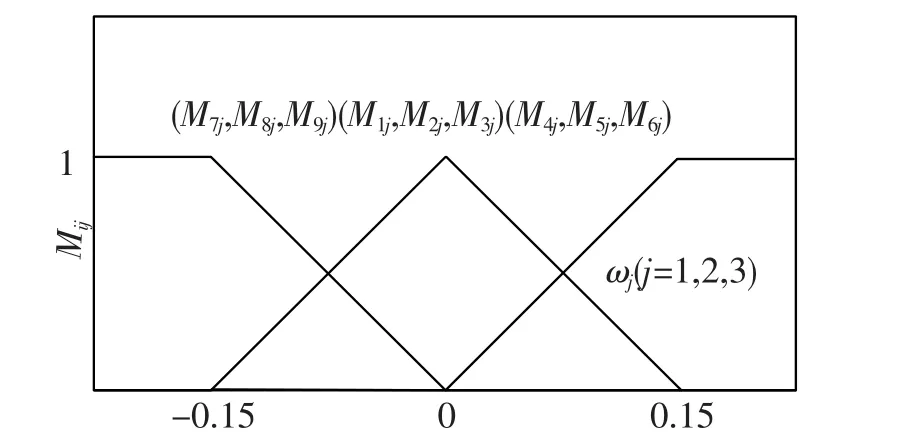
图3 隶属函数Mij(i=1，2，…，9，j=1，2，3)

按照前节的设计方法，分别在A，B两种条件下的设计TS模糊模型H∞最优故障观测器，对比传统线性H∞观测器、A情况TS模型H∞最优故障观测器和B情况TS模型H∞最优故障观测器，故障一的仿真结果如图4～6所示，故障二的仿真结果如图7～9所示.

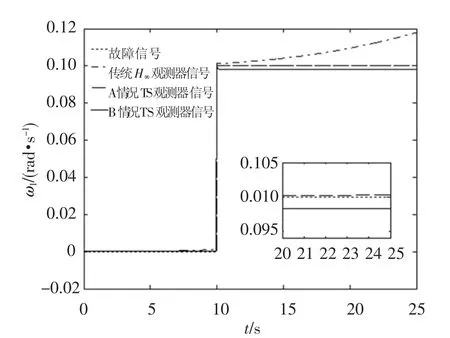
图4 滚动轴常值故障和估计

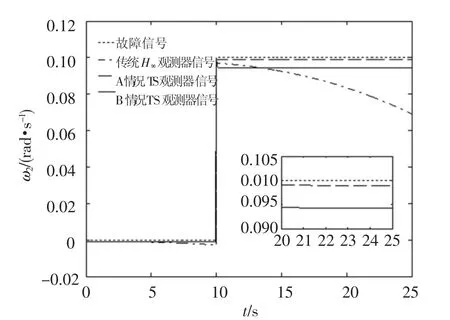
图5 俯仰轴常值故障和参数估计

由图4～图6可以看出，当系统受故障长时间影响，系统状态发生较大变化偏离平衡点，传统线性H∞观测器的故障估计值逐渐偏离真实故障常值，而两种基于TS模型的H∞最优故障观测器却能够较好地跟踪故障信号.图7～图9同样显示，本文所设计的观测器对于周期信号也具备良好的鲁棒特性.

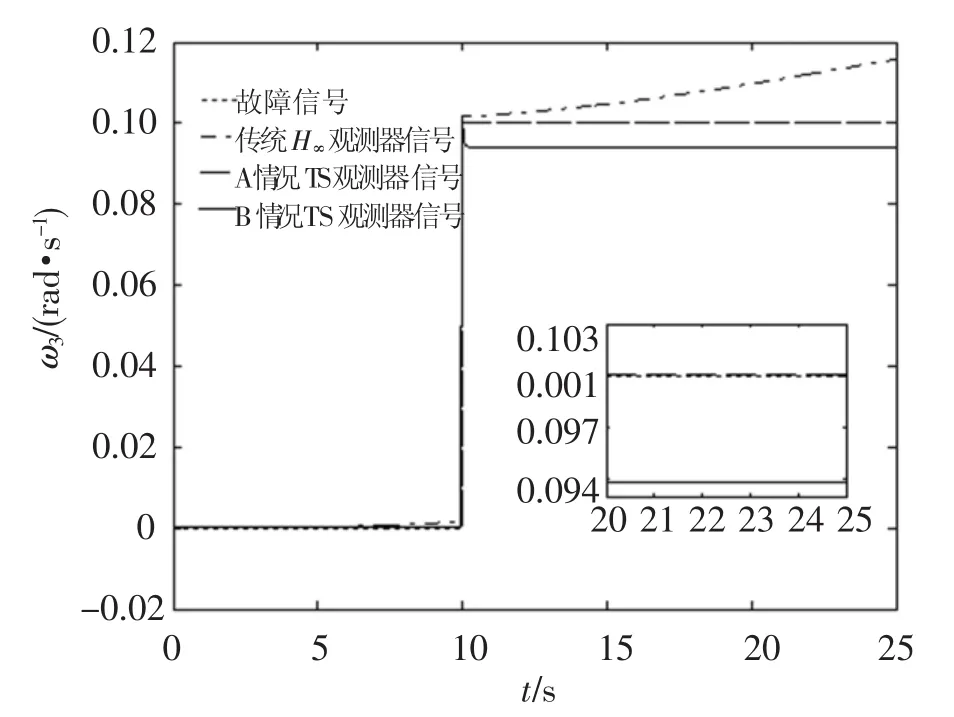
图6 偏航轴常值故障和参数估计

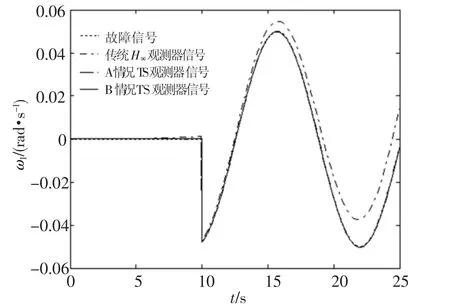
图7 滚动轴周期故障和估计

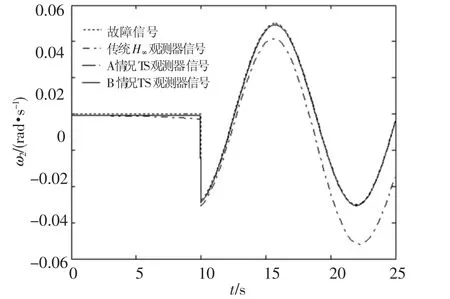
图8 俯仰轴周期故障和参数估计

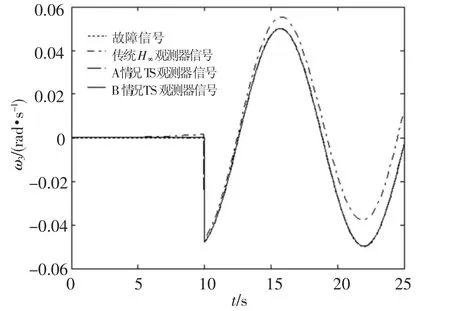
图9 偏航轴周期故障和参数估计

从图4～图6的子图中看到，情况A下的观测器的静态性能总体上要好于情况B下的观测器，但由于故障发生时，实际系统状态不可直接测量，即先验知识未知.所以后者在实际应用中具有更好的可行性.

在设计观测器前，假设3要求提前知道观测器增益范数，这在实际设计中是难以实现的.但因为情况A中观测器增益小，而情况B实质是对理想情况A的逼近，故在实际设计中忽略γL项.构造常数ε值是根据仿真实验效果选取的.这是因为假设1要求系统状态保持在一个有限的范围之内，但当系统发生故障时间足够长，系统的状态仍然可能会超出构造变量ε给定范围;同时设定过大的边界值也有可能导致H∞问题无解.

另外，模糊函数hi(x)，hi()均具有强非线性，状态变量偏离平衡点过大或初始TS工作点选取不当均有可能使得观测失效.幸运的是，实际飞轮输入相对较小，这使得在观测器失效前有足够的时间检测和隔离陀螺故障.

4 结论

本文针对卫星姿态控制系统陀螺故障诊断问题，给出两种鲁棒模糊诊断方案.先将卫星模型转化为TS模糊模型，将故障诊断问题转化为H∞最优观测器设计问题，采用并行分布补偿设计观测器结构，使用H∞工具箱求得动态观测增益，有效诊断和分离了陀螺故障.利用TS模糊模型和H∞最优观测器设计故障诊断的方法结构简单，容易实现.数学仿真结果验证了该算法的可行性和有效性.

［1］FRANK P M.Fault diagnosis in dynamic systems using analytical and knowledge-based redundancy-a survey and some new results［J］.IEEE Transactions on Automatic Control，1990，26(3):459－474.

［2］WANG H，HUANG Z J，DALEY S.On the use of adaptive updating rules for actuator and sensor fault diagnosis［J］.IEEE Transactions on Automatic Control，1997，33(2):217－225.

［3］DEMETRIOU M A.Robust adaptive techniques for sensor fault detection and diagnosis［C］//Proceedings of 37thIEEE Conference on Decision and Control.Tampa，USA:IEEE Control Systems Society，1998:1143－ 1148.

［4］CHEN J.Robust Residual Generation for Model-based Fault Diagnosis of Dynamic Systems［D］.UK:The University of York，1995.

［5］FRANK P M，DING X.Frequency domain approach to optimally robust residual generation and evaluation for mode-based fault diagnosis［J］.IEEE Transactions on Automatic Control，1994，30(6):789－804.

［6］PATTON R J.Robustness in model-based fault diagnosis:The 1995 situation［J］.Annual Reviews in Control，1997，21(1):103－123.

［7］VEMURI A T，POLYCARPOU M M.On the use of online approximators for sensor fault diagnosis［C］//Proceedings of American Control Conference.Philadelphia1，USA:IEEE Control System Society，1998:2857－2861.

［8］NIKOUKHAH R.Innovations generation in the presence of unknown inputs:Application to robust failure detection［J］.IEEE Transactions on Automatic Control，1994，30(2):1851－1867.

［9］PERTEW A M.Nonlinear Observer-based Fault Detection and Diagnosis［D］.Canada:University of Alberta，2007.

［10］TANAKA K，WANG H O.Fuzzy Control Systems Design and Analysis［M］.New York:John Wiley＆Sons Press，2001.

［11］SONG B，MA G F，LI C J.Robust fuzzy controller design for a rigid satellite attitude regulation system［C］// 1stInternational Symposium on Systems and Control in Aerospace and Astronautics.Harbin，China:Institute of Electrical and Electronics Engineers Computer Society，2006:424－429.

［12］CHEN W T，SAIF M.Design of a TS based fuzzy nonlinear unknown input observer with fault diagnosis applications［C］//Proceedings of American Control Conference.Washington，USA:IEEE Control System Society，2007:2545－2550.

［13］SIDI M J.Spacecraft dynamics and control［M］.London:Cambridge University Press，1997.

［14］DOYLE J，GLOVER K，KHARGONEKAR P，et al.State space solutions to standard H2and H∞control problems［J］.IEEE Transactions on Automatic Control，1989，34(8):1851－1867.

［15］ZHOU K，DOYLE J C.Essentials of Robust Control［M］.New York:Prentice-Hall Press，1998.