基于蒙特卡洛法的反舰导弹末端机动突防效果研究

范作娥，顾文锦，姜 鹏，马培蓓

（1.海军航空工程学院 控制工程系，山东 烟台 264001；2.91065 部队，辽宁 葫芦岛 125001）

0 引言

随着舰空导弹武器系统的不断发展，反舰导弹的突防问题变得越来越重要。为了增加对反舰导弹的拦截难度，提高反舰导弹的突防能力，反舰导弹需要进行末端机动。关于反舰导弹末端机动的控制与导引方法研究，以及各种机动方式的研究，国内外已经有相关的公开发表文献[1-5]。相应地，针对反舰导弹各种机动方式的突防效果的评估，也越来越受到学者们的关注。文献[4]以突防概率作为评价标准，研究了突防导弹作正弦摆动突防机动时的突防效果。文献[5]利用共轭系统和拉氏变换技术，研究了反舰导弹的螺旋机动和摆式机动的突防效果。这些文献大多是应用伴随技术，针对两维平面内导弹与目标之间的相对运动方程，通过求解拦截导弹的脱靶量解析解，研究机动突防持续时间对稳态脱靶量的影响，从而进一步研究对导弹突防概率有多大贡献。但是，用伴随技术来研究反舰导弹末端机动对突防概率有多大影响的时候，考虑到的实际对抗条件比较少，而且不能比较不同的末端机动方式之间，哪种方式最好。

本文就是从工程应用的角度出发，在考虑尽可能多的实际影响因素的条件下，针对反舰导弹在有舰空导弹拦截的情况下，进行全弹道打靶仿真，采用蒙特卡洛法计算反舰导弹在不同机动方式下（含蛇行机动、摆式机动、螺旋机动）的突防概率，从而比较各种机动方式的优劣。当反舰导弹进行末端机动之前，其控制系统的设计采用的是过载控制方法[6-7]，在末端机动开始之后，采用的是过载控制与位置控制结合的复合控制方法[8]。

1 反舰导弹末端机动一体化控制

反舰导弹末端机动一体化控制的原理主要是，在导弹进行末端机动的时候，同时引入过载控制与位置控制，分别将它们作为宏观与微观的控制手段。在宏观上，过载控制预先给定了运动的趋势；在微观上，由位置反馈形成闭合系统，消除位置上细小的偏差。这样的复合控制手段在仿真中取得了单独过载控制与单独位置控制均无法达到的控制效果，并且鲁棒性比较强[8]。

1.1 末端机动期望轨迹描述

末端机动轨迹是导弹质心相当于地面坐标系OXYZ的运动轨迹，通常是根据飞行的距离x 进行控制的，即以变量x为参数，此时，描述末端机动轨迹的位置参数方程形式为：

根据制导理论，在拦截前的恰当时间如果目标实施最大加速度机动，就能够产生足够大的脱靶量。通常，目标是不知道拦截导弹系统参数的，也不知道拦截时间，那么周期性的机动加速度是目标的一种最佳生存策略。本文用到的非平面机动方式（如摆式机动、螺旋机动）同样是反舰导弹周期性地改变飞行轨迹，机动轨迹在纵向平面和航向平面内的投影可分别用如下形式的正弦曲线和余弦曲线来近似表示：

式中：(x1y1z1)为末端机动的初始位置；ξ0为初始相位角，这里取 ξ0=− π /2；ly、lz分别为纵向和航向投影曲线的机动半径；kyπ、kzπ分别为一个机动周期内纵向和航向投影曲线的相位变化值；A称为节距，它是指在一个机动周期内反舰导弹沿地面坐标系OX轴方向飞行的距离。

定义节点数n，它是在末端机动范围内反舰导弹所完成的机动周期的数值。

考虑到末端机动是根据x 进行控制的，假设反舰导弹在飞行到 x=x2时停止机动，则有：n=(x2− x1)A。式中，ly、lz、ky、kz、A为末端机动参数，根据具体的末端机动方式进行选取。若选取 ly=0，则表示航向蛇行机动轨迹，z 随x 按余弦曲线周期性地变化。由此可见，平面机动方式是非平面机动方式的特例。

1.2 末端机动一体化控制模型

由于末端机动中的控制信号包括法向过载和质心两组控制信号。因此，末端机动的一体化控制模型也应该包括这两组控制信号。即内环的法向过载控制信号 n∗y和 n∗z，以及外环的质心控制信号 y*和z*。具体的控制信号如下[7]：

其中，

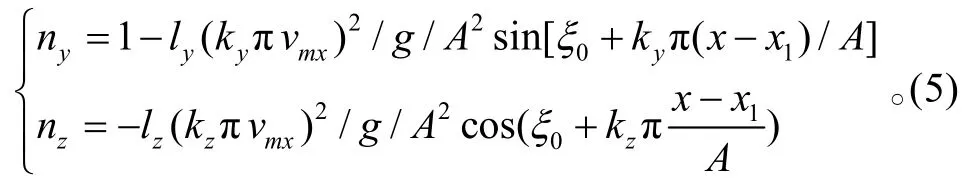
公式(3)～(5)中，ny、θ 及vψ是导弹的飞行力学参数，具体见文献[9]。上述两种控制信号相互配合、协调控制，即可控制反舰导弹完成预定的各种末端机动弹道。末端机动的起始位置及机动范围视具体情况定。

2 反舰导弹与舰空导弹对抗模型

2.1 舰空导弹截击反舰导弹航向平面模型

如图1所示，OXYZ为地面坐标系，反舰导弹M点的位置为(x,y,z)，拦截弹I点的位置为(xI,yI,zI)，实际的弹（拦截弹I）目（反舰导弹M）之间的距离大小为：

图1 航向平面拦截关系

在航向平面内，各角度的正方向的规定一样，见图1。图中，Rxz为弹目距离，qxz为视线角，v 和vI分别为反舰导弹与舰空导弹的速度，ψM和ψI分别为两者的弹道偏角，ηM和 ηI分别为两者的前置角，即各自的速度矢量方向转到视线方向所要旋转的角度。

由图1建立航向平面内的拦截几何关系：

式(7)、(8)中：

当 x ＞ xI，即拦截导弹尾追反舰导弹情况时，

2.2 舰空导弹截击反舰导弹纵向平面模型

图2中 zI轴的指向与OZ轴指向相反是因为舰空导弹弹道偏角| ψI| ＞ π/2。θM和 θI分别为反舰导弹和舰空导弹的弹道倾角，顺时针转动为正，其他都是逆时针转动为正，故 θI＜0、视线角 qxy＜0，并且这两个角度的正方向相反。前置角 ηI＞ 0，ηM＜0。

图2 纵向平面拦截关系

纵向平面内的拦截几何关系：

式(12)、(13)中：

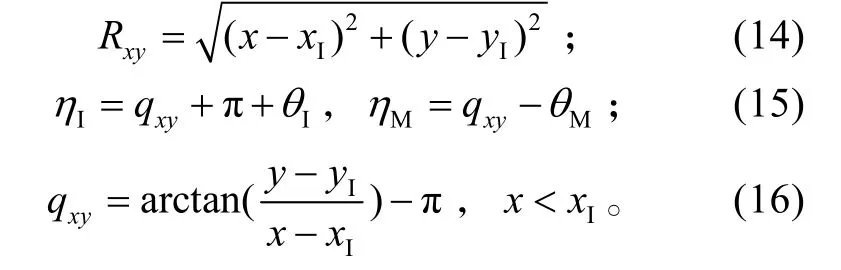
当 x ＞ xI，即拦截导弹尾追反舰导弹情况时，

3 舰空导弹的制导系统

鉴于舰空导弹的相关信息我们无法详细知道，故在舰空导弹拦截反舰导弹的过程中，将舰空导弹视为质点，只进行质心运动，其运动方程[9]：

考虑舰空导弹的制导控制系统动态过程，将其简化为3个1 阶惯性延迟环节，其简化动态过程如图3所示，其中 T1=0.01 s为导引头的时间常数；T2=0.02 s为控制回路的时间常数；T3=0.5 s为舰空导弹弹体的时间常数。

舰空导弹（拦截弹I）采用如下的比例导引律：

式中，N1与N2为舰空导弹的比例导引系数。

图3 制导控制系统简化图

4 舰空导弹与反舰导弹的对抗仿真

在进行反舰导弹与舰空导弹的突防对抗仿真过程中，由于反舰导弹采用的是全弹道仿真模型，舰空导弹采用的是简化模型，所以，为了使仿真结果尽可能的接近事实，反舰导弹考虑了多种外界及内部干扰的影响，舰空导弹也考虑了一些本身的结构约束，具体的叙述见下文。

4.1 反舰导弹所受干扰

1）海浪影响

反舰导弹飞行过程中，通过无线电高度表来测量导弹距海面的高度，送入惯导回路，计算得到组合高度，与装订高度进行比较，再根据高度控制方程进行高度控制。由此可见当海面波动时，无线电高度表的测量高度会因测量面的变化而变化，从而对导弹的高度控制产生影响，特别是在较大风浪时，导弹有可能因触浪而导致反舰导弹掉海，因而必须对海浪进行模拟。在工程上，一般把海浪看作一种具有各态历经性的平稳正态随机过程，利用频谱方法来进行研究。本文采用如式(20)所示的一维PM海浪谱作为海浪模型[10]：

式中：HS为海浪有效波高，单位m（由海情定，本文采用四级海情 HS=2.5 m）；ω为海浪角频率。

根据式(20)，采用波浪叠加法对海浪进行仿真，即可得出海浪的瞬时波动 ξ (t)，则导弹相对海平面的瞬时飞行高度为

式中：yw(t)为考虑海浪波动的情况下导弹的飞行高度；y (t)为不考虑海浪波动的情况下导弹的飞行高度。

将导弹相对海平面的瞬时飞行高度代入导弹的导航模块，从而可模拟海浪对导弹高度控制的影响。

2）建模不确定性影响

由于反舰导弹在飞行过程中，其飞行运动参数受干扰或建模不确定性等影响，其运动参数需要进行一定的摄动，故对其采用确定型随机处理，使运动参数相对标称运动参数进行最大幅度±30%的摄动。

3）高度表测量误差

反舰导弹的控制系统的组成除了惯性导航系统外，还有必要的弹上测量仪表，例如高度表。反舰导弹在飞行过程中，通过雷达高度表来测量导弹距海面的高度，以此与装订高度进行比较。因此，高度表的测量误差应该在仿真对抗中被考虑进去，对测量高度值采用确定型随机处理，进行±1%的摄动。

4）导弹结构装备误差

由于导弹本身的控制系统和导航系统就是一个非常复杂的综合系统，由其本身的结构装备引起的干扰和误差，对其力和力矩肯定产生一定的影响，从而对导弹的控制系统也会产生一定的影响。因此，在对抗仿真过程中，对干扰力和力矩也采用确定型随机处理，进行±1%的摄动。

5）指挥仪初始方位误差

由于指挥仪的初始方位也是有仪器进行测量得来的，其初始方位角毫无疑问也会带有误差，故对其也采用确定型随机处理，对其测量值进行±1%的摄动。

6）陀螺漂移影响

反舰导弹的控制系统中，因陀螺仪在测量角度的过程中带有漂移，故陀螺漂移所引起的ψ值有所变化，在对抗仿真中考虑陀螺漂移速度1 n mile/h。

4.2 舰空导弹所受约束

1）导引头前置角约束

设定舰空导弹的导引头有前置角约束范围：−5 0° ～ + 50°。当前置角达到此限制范围之外时，导引头失效，舰空导弹沿失效点的方向作直线运动。

2）导引头盲区约束

设定舰空导弹的导引头盲区为500 m，即导弹进入死区后，导引头失效，舰空导弹沿失效点的方向作直线运动。

4.3 仿真条件

当反舰导弹在地面坐标系内沿OX轴方向飞行到Xstart的时候，开始以纵向ly和航向lz投影曲线机动半径分别进行不同方式的末端机动（航向蛇行、纵向蛇行、摆式机动和螺旋机动），与此同时，舰空导弹由初始位置（xI，yI，zI）开始，以相同的初始飞行速度vI进行拦截。反舰导弹开始进行变轨机动时的初始相位角为0ξ，且在一个机动周期内，反舰导弹沿OX轴方向飞行的距离为A。

值得注意的是，反舰导弹进行不同方式的变轨机动时，各种变轨方式在航向和纵向投影曲线的最大机动半径是相同的，即ly=lz=200 m。只有进行摆式机动的时候例外，其纵向投影半径为ly=50 m。设Xstart=240 km，vI=850 m/s，ξ0=−π/2，A=7 000 m。

4.4 仿真结果与分析

在上述的仿真条件下，进行舰空导弹拦截反舰导弹的对抗仿真，当舰空导弹的拦截初始位置不同时，给出如下两种仿真结果：

1）当舰空导弹初始拦截位置（xI，yI，zI）为xI=265 km、yI=80 m、zI=1 000 m时，进行不同机动方式的拦截对抗仿真，脱靶量数据结果见表1。

表1 拦截导弹对不同机动方式反舰导弹的脱靶量之一

2）当舰空导弹的初始拦截位置（xI，yI，zI）变为xI=244 km、yI=80 m、zI=19.66 km时，进行不同机动方式的拦截对抗仿真，脱靶量数据结果见表2。

表2 拦截导弹对不同机动方式反舰导弹的脱靶量之二

由表1、2 中的仿真数据看出，应用过载控制方法设计的反舰导弹，在有舰空导弹拦截的情况下，进行不同的末端机动方式进行突防的时候，拦截导弹的脱靶量要比不进行末端机动的时候高。同样，反舰导弹进行带有纵向机动的变轨方式，拦截导弹的脱靶量要明显高于只进行航向时的机动方式。

但是由于纵向蛇行、摆式机动和螺旋机动这三种方式，其脱靶量差距不是很大，而且没有明显的规律可寻，所以要想比较那种方式比较好，仅仅通过相同条件的一两次仿真，不足以说明问题，这将是下一节要解决的问题。

5 基于蒙特卡洛法的突防概率研究

本节主要是在前面模型和仿真基础上，在反舰导弹进行不同形式的末端机动时候，舰空导弹由不同的初始位置进行拦截，在计算机上进行多次打靶仿真，采用蒙特卡洛法，针对打靶数据计算各种末端机动方式的突防概率，比较末端直线运动、航向蛇行机动、纵向蛇行机动、螺旋机动和摆式机动，那种机动方式的突防概率最高。

5.1 仿真条件

利用蒙特卡洛法来计算反舰导弹的突防概率，比较各种末端机动方式的优劣，需要不同的初始仿真条件下，在计算机上进行多次打靶仿真，具体的初始条件的选取，如图4所示。图中所示坐标系为地面坐标系中的XOZ 平面，M为反舰导弹的位置，其坐标为（xstart，0），I为拦截弹的位置，其坐标为(xI,zI)，反舰导弹与舰空导弹之间的距离为R1，舰空导弹的初始方位角为ψL。

图4 初始拦截位置图

当反舰导弹沿OX轴方向飞行到xstart时，开始进行不同方式的变轨机动，与此同时，舰空导弹由初始拦截位置 (xI,zI)开始，以飞行速度vI对反舰导弹进行拦截，仿真中用到的反舰导弹的相关参数同第4节相同，不同的只是舰空导弹的初始拦截位置及初始方位角不同。关于舰空导弹初始拦截条件的选择，遵循如下两种选择方法：

1）针对每一种末端机动方式，在舰空导弹的初始方位角ψL相等的情况下，按照不同的反舰导弹与舰空导弹之间的距离 R1，来定义舰空导弹的初始拦截位置。其中，R1分别选择为10 km、20 km 和30 km，这样就定义了3个初始拦截条件。

2）针对每一种末端机动方式，在反舰导弹与舰空导弹之间的距离 R1相等的情况下，按照不同的舰空导弹的初始方位角ψL，来定义舰空导弹的初始拦截位置。其中，ψL在(0 ～360°) 范围内，由0°开始，每隔5°选择一次，定义为一个初始拦截条件，这样就定义了72个初始条件。

联合上述两种初始拦截条件的选择方法，可以得出每一种末端机动方式共有216种不同的初始仿真条件，即每一种末端机动方式都要进行216次打靶仿真。由于每种末端机动方式都需要进行216次打靶，所以，要想比较各种末端机动方式的优劣（直线飞行、航向蛇行、纵向蛇行、摆式、螺旋机动），就需要总共进行1 080次打靶仿真。

5.2 仿真结果与分析

在上述初始仿真条件下，进行拦截对抗仿真，总共得到舰空导弹1 080个脱靶量。以杀伤半径5 m来定义命中区，即舰空导弹的脱靶量只要小于5 m，就当作舰空导弹成功拦截反舰导弹。针对这些记录的不同机动方式的打靶数据，计算整理反舰导弹的突防概率如表3所示。

表3 不同机动方式的突防概率

对比仿真数据表1～3，看出表2、3的仿真结果完全对应，但表1中，纵向蛇行机动的脱靶量为18.455 m，而螺旋机动的脱靶量为15.978 m，这与表3中的仿真结果不相符。造成这种结果的主要原因是，反舰导弹在进行纵向蛇行机动时，如果反舰导弹飞行在正弦曲线的峰值点，这时横向过载最大，就会造成大脱靶量，但它只是蛇行飞行状态下的一种个例，其他情况都是以小横向过载来飞行；而进行螺旋机动的时候，反舰导弹时时刻刻都是以最大过载飞行，因此从统计数据中来看，纵向蛇行机动的突防概率仍然小于螺旋机动的突防概率。

由表3还可以看出，同样是进行平面机动，纵向蛇行机动的突防概率为71.76%，要明显高于航向蛇行机动的突防概率为41.2%。造成这种结果的原因是，在对抗仿真的过程中，舰空导弹在拦截进行纵向蛇行机动的反舰导弹的时候，容易掉海，这就造成了纵向机动的突防概率明显高于航向机动。

由仿真结果和分析得出，在有舰空导弹拦截的情况下，关于反舰导弹突防概率有3个结论：① 反舰导弹进行末端机动的突防概率，要比末端直线飞行的时候大；② 反舰导弹进行纵向平面行机动的突防概率，要比航向平面机动的时候大；③ 反舰导弹以不同的末端机动方式突防的时候，按照突防概率的大小，机动方式由优至劣的顺序是：螺旋机动—摆式机动—纵向蛇行机动—航向蛇行机动—直线飞行。

6 结束语

本文从工程应用的角度出发，在考虑尽可能多的实际影响因素及约束条件的影响下，建立了反舰导弹在有舰空导弹拦截情况下的对抗模型，针对上述模型，在舰空导弹不同拦截初始条件下，进行了上千次全弹道打靶仿真，应用蒙特卡洛法，以打靶试验数据为依据，比较直观全面的比较了各种末端机动方式的突防效果，这在工程上具有较大实用参考价值。但是，本文在建模过程中，舰空导弹采用的是简化模型，因此，如何将舰空导弹模型扩展为全弹道仿真模型，并在此基础上考虑舰空弹的实际影响因素，使得仿真数据更接近工程应用，将是进一步研究的课题。

[1]IMADO F,MIWA S.Missile guidance algorithm against high-g barrel roll maneuvers[J].Journal of Guidance,Control,and Dynamics,1994,17(1):123-128.

[2]顾文锦,毕兰金,武志东.基于伴随技术的超音速反舰导弹末端机动突防的脱靶量分析[J].海军航空工程学院学报,2009,24(4):400-404.

[3]周狄,邹昕光,孙德波.导弹机动突防滑模制导律[J].宇航学报,2006,27(2):213-216.

[4]姜玉宪,崔静.导弹摆动式突防策略的有效性[J].北京航空航天大学学报,2002,28(2):133-136.

[5]顾文锦,赵红超,王凤莲.反舰导弹末端机动的突防效果研究[J].宇航学报,2005,26(6):758-761.

[6]赵红超,顾文锦,马登武.飞航导弹基于输出重定义的变结构控制[J].兵工学报,2005,26(6):783-786.

[7]赵红超,顾文锦,王瑞奇.反舰导弹的自适应全局滑模变结构控制[J].控制工程,2005,12(4):320-322.

[8]顾文锦,赵红超,王凤莲.导弹末端机动的一体化控制模型[J].宇航学报,2004,25(6):677-680.

[9]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2000:53-57.

[10]赖志昌,金鸿章,李国斌,等.随机海浪作用下的船舶横摇减摇预报方法[J].哈尔滨工程大学学报,2001,22(3):13-16.