基于聚类和Hough变换的多编队航迹起始算法
2010-03-24邢凤勇王海鹏
邢凤勇,熊 伟,王海鹏
(海军航空工程学院 电子信息工程系,山东 烟台 264001)
杂波环境下的密集多目标跟踪[1]是多传感器多目标跟踪领域的难点,特别是所跟踪目标的空间位置距离很近、运动方式大致相同时,不仅回波众多,而且关联门交叉严重,要对其进行精确跟踪十分困难[2]。当所跟踪目标由多个个体组成时,它们所展现出的主要特点是一种群运动[3],因而在目标跟踪领域形成了一种新的跟踪问题,即编队目标跟踪。
编队被定义为方向、距离和速度满足以下3个条件的多个目标:① 运动方向一致;② 编队中各成员之间的距离远远小于各编队之间的距离;③ 速度基本相同。[4]
航迹起始是航迹处理中的首要问题,但同跟踪维持的研究相比,航迹起始课题方面的研究成果非常少。由于航迹起始时,目标一般距侦察站很远,传感器探测分辨力低、测量精度差[5],加之真假目标的出现无真正的统计规律。因此,在多目标航迹处理中,航迹起始问题是难以处理的问题。
由定义可知,编队目标的运动中各个成员之间都是基于固定相对位置,即它们有固定几何结构。在雷达分辨力高或编队目标分布稀疏的情况下,可以区分辨出编队的几何结构[6],此时的编队目标航迹起始可以通过判别这种具体的结构来达到剔除编队中杂波的目的。但在现代战争中,编队目标的密集度有增无减,群中各目标空间距离很小,当雷达的分辨力较低时,容易造成量测的丢失。测量噪声和过程噪声的存在使得普通雷达很难分辨编队中的各个成员,而编队结构也就不得而知,以上提到的编队跟踪的结构优势就不能作为编队目标跟踪和航迹起始的判断依据。在这种情况下,本文提出并改进了一种易于实现的、计算量较少的基于K均值聚类[7]和Hough变换的编队目标航迹起始算法。
1 传感器回波的循环阈值聚合
通过比较两个量测的空间距离[8]与一个常数之间的大小关系可以完成传感器回波的分割,假定Z (k)为传感器在k时刻所获得的量测集,且
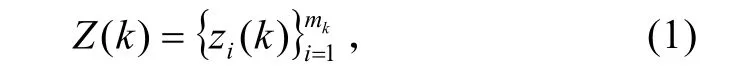
式中,mk为k时刻的量测个数。
定义1:Z(k)中第i个量测 zi(k)=[xik,yik]'与第j个量测 zj(k)的距离为:
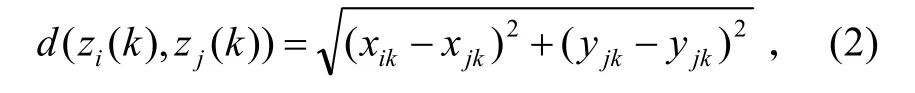
若
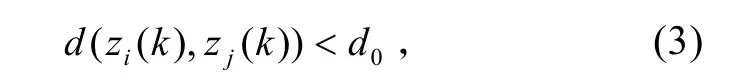
则量测 zi(k)和zj(k)属于同一个子群。其中,d0反映了编队内目标的稠密程度,其取值与传感器系统编队目标跟踪的目的有关。对机械扫描雷达而言,采用编队目标跟踪的目的是解决错误互联所引起的滤波误差协方差增大的问题,故 d0为最近邻域法刚好不能区分的两个目标之间的空间距离。
编队目标分割可分为以下4步[9]:
1)选取 zi(k)为中心,以 d0为阈值建立波门;
2)对落入波门中的每个量测重新以 d0为阈值建立波门,寻找落入最新波门中的量测;
3)重复第2)步,直到所建的波门中没有量测为止,在此过程中所涉及到的量测定义为一个子群;
4)从不属于已确定子群的量测中任意选取一个量测,重复以上3步直到最后一个量测,最终完成对雷达回波的分割。
2 K均值聚类的子群中心点算法
定义2:设X是数据集,即
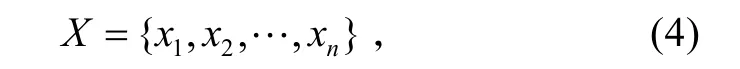
定义X的m 聚类ℜ,将X 分割成m个集合(聚类)C1,…,Cm,使其满足下面3个条件:
而且,在聚类中包含的向量彼此“更相似”,与其他类中的向量“不相似”。
K-均值聚类[10]是一种迭代的聚类算法,迭代过程中不断地移动簇集中的成员直至得到理想的簇集为止。K-means算法工作过程如下:
首先,从n个数据对象任意选择k个对象作为初始聚类中心,而对于所剩下的其他对象,则根据它们与这些聚类中心的相似度(距离),分别将它们与其最相似的(聚类中心所代表的)聚类;其次,再计算每个所获新聚类的中心(该聚类中所在对象的均值),不断重复这一过程,直到标准测度函数开始收敛为止。相似度通过距离公式进行计算,常用的距离有Minkoski距离、Euclid距离、Chebyshev距离、Mahalanois距离等。在此以欧氏距离作为距离计算公式如下:
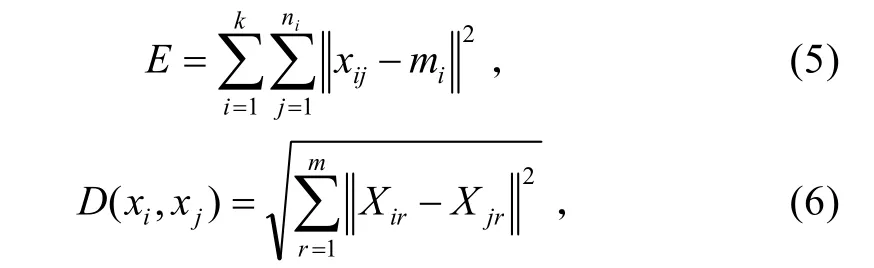
式(5)中:xij是第i类第j个样本;im是第i类的聚类中心或称质心;in是第i类样本个数。
K-均值聚类算法实质就是通过反复迭代寻找k个最佳的聚类中心,将全体n个样本点分配到离它最近的聚类中心,使聚类误差平方和E最小。
K-均值聚类法实施流程图如下[11]:
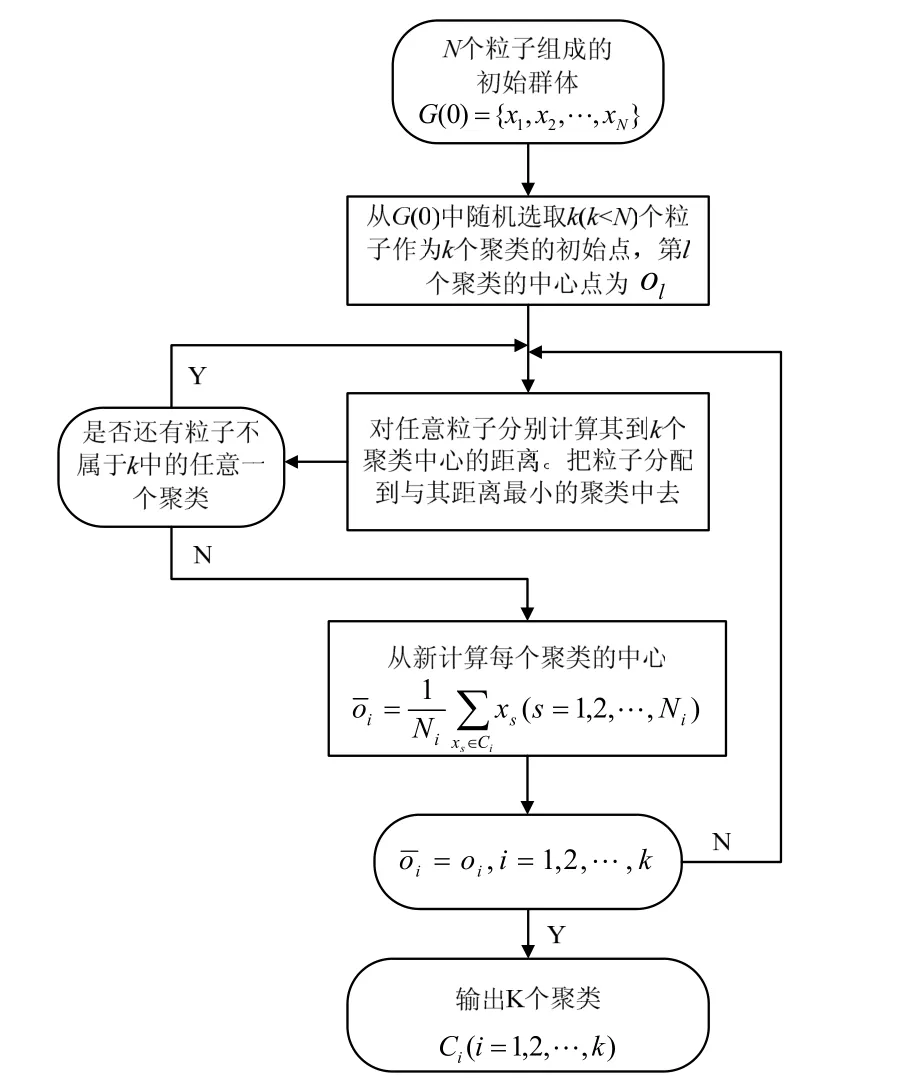
图1 K-均值聚类法流程图
3 编队目标互联的杂波群去除
设量测集Z(k)最终分割为m个编队,记为{U1,U2,…,Um}。在通过K-均值聚类法获得相邻时刻各个编队的中心之后,定义k=m时刻第i个编队的中心与k=n时刻第j个编队的中心的距离为
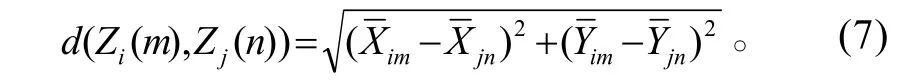
若这两个编队互联,则必须满足下式
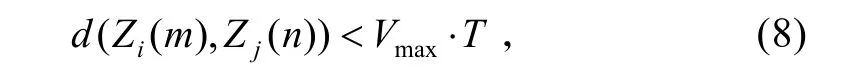
式(8)中:T为采样间隔;n=m+1;Vmax为编队的最大速度,其取值视具体编队类型而定。
如果k=m时刻第i个编队与k=n时刻的多个编队互联,选取距离最近的编队为互联编队。
4 Hough变换的编队目标航迹起始
将极坐标引入Hough变换,得到其变换函数:
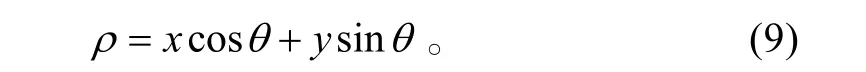
如图2所示,数据空间中的—条直线可以通过从原点到这条直线的距离ρ和ρ与x轴的夹角θ 来定义。
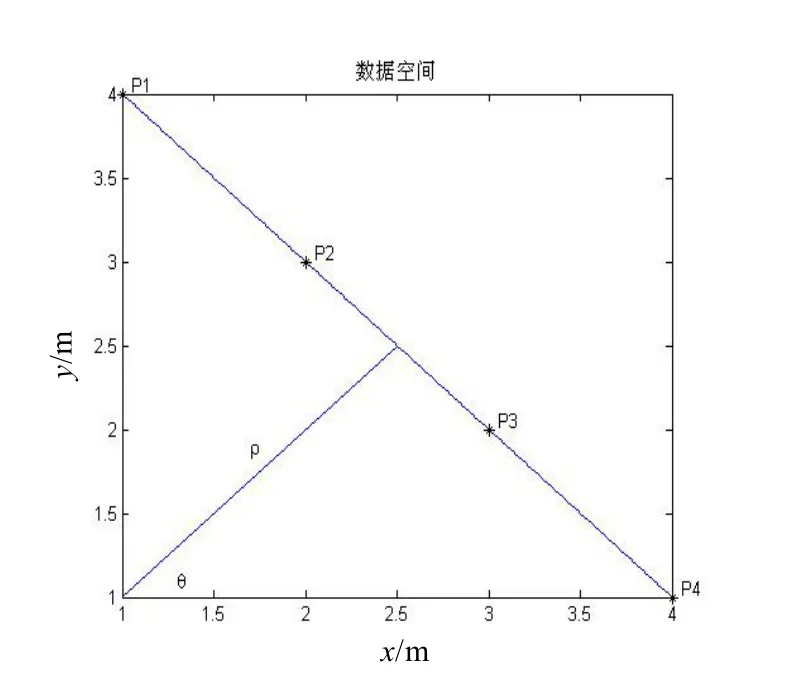
图2 数据空间上的4个点
如图3所示,P1、P2、P3、P4 经公式(9)变换到参数空间并在参数空间相交于一点。
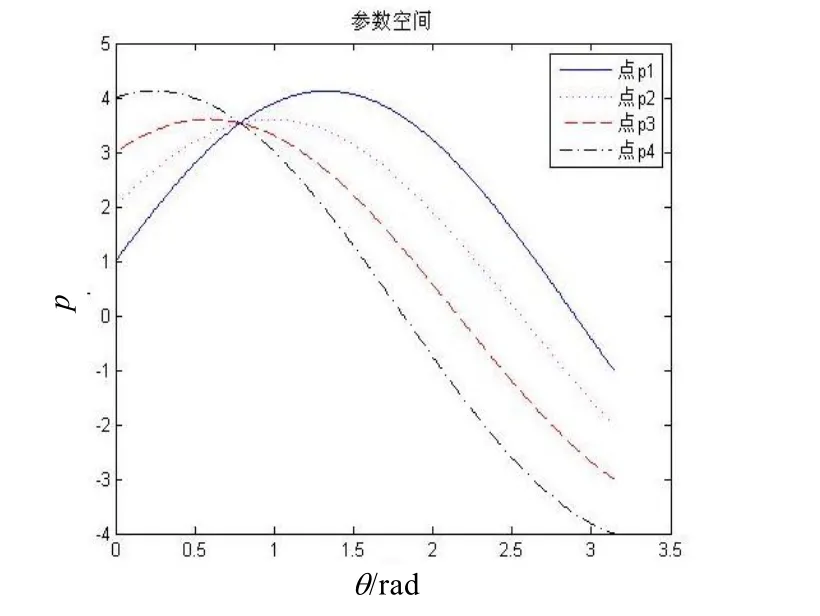
图3 数据空间变换到参数空间后的点迹
在参数空间中交于公共点的曲线所对应的直角坐标系中的坐标点一定在一条直线上。Hough变换基本算法采用参考文献[12]。
5 仿真验证与分析
为验证本文所提出的K均值聚类和Hough变换的密集多编队航迹起始算法的有效性,本文对两个编队共10个目标的航迹起始进行了仿真验证。
5.1 仿真环境与结果
本节假定编队目标的起始在如下环境中进行:过程噪声分量q=0.01;测距误差rσ=90 m;测角误差 θσ=0.03 rad;检测概率 DP=0.997;门概率GP=0.97;采样间隔T=1 s;仿真中每个周期的杂波个数按照泊松分布确定的,取λ=50;每次仿真步数40步。在该环境下对10个目标进行航迹起始,前5个目标组成第一个编队,编队中每个目标的初始位置均在(1 500 m,2 000 m)与(0 m,500 m)中随机产生,初始速度为(270 m/s,270 m/s);后5个目标组成第二个编队,编队中每个目标的初始位置均在(0 m,500 m)与(1 500 m,2 000 m)中随机产生,初始速度为(270 m/s,270 m/s)。
图4~6为量测空间的目标点迹以及聚类后的群中心点,图7为变换到参数空间Hough变换图,图8为量测航迹和编队航迹对比图。
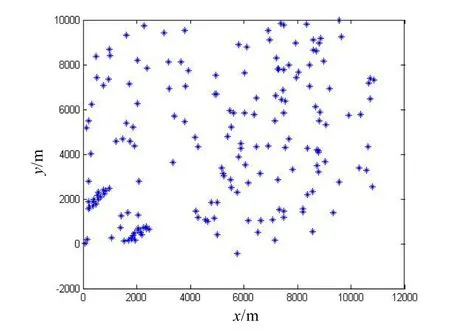
图4 前3个时刻传感器回波
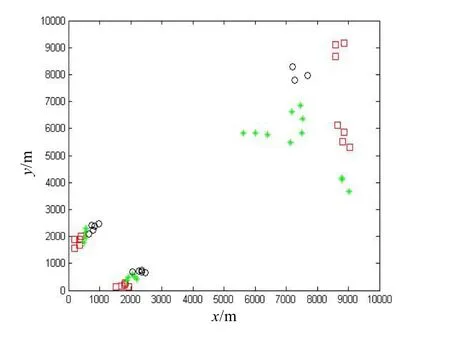
图5 聚合后的前3个时刻传感器回波
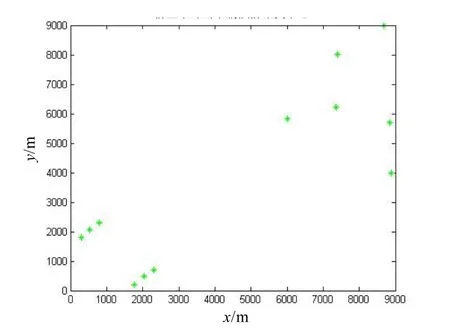
图6 K-均值聚类的各子群中心
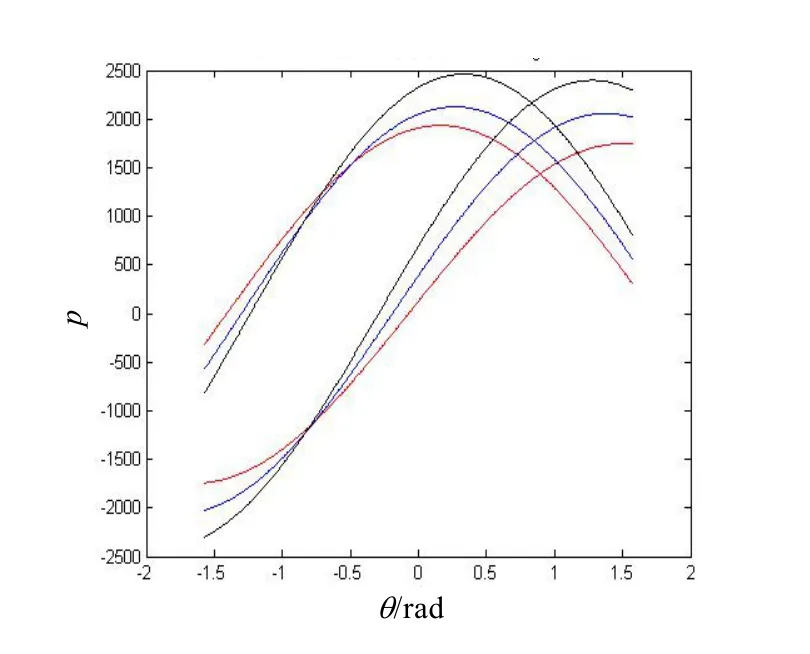
图7 互联上的两条航迹的Hough变换
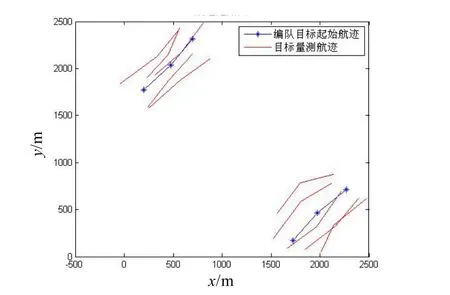
图8 航迹起始图
5.2 仿真分析
图4为低分辨率传感器对两个密集编队共10个目标的量测点迹图,可以明显看出前3个时刻目标明显分成两个编队,编队内部各目标间没有固定的几何结构。目标回波较为密集,而杂波分布较为分散,所以在循环阈值聚合中去除了大量在观测空间内均匀分布的杂波,这同时也是编队目标跟踪中可以用来去除杂波的重要特征。
图5前3个时刻传感器回波通过循环阈值聚合后形成的空间子群分布态势图。这里设同一子群中两个量测点判为一个子群的最大距离为230 m,不但目标点聚合成为子群,而且距离较近的杂波点也聚合成了子群,分布分散的杂波点迹得到了消除。
图6对聚合后的子群代入K-均值聚类法,形成各个子群的中心。图中前3个时刻形成的航迹已经比较清晰,杂波子群中心间的距离都远远大于目标以最大速度在采样间隔间的运行距离,所以通过中心外推法又进一步去除了杂波子群。
图7对互联上的前3时刻子群中心点变换到参数空间中去,6条曲线相交于两个点,每个交点的3条曲线分别代表3个时刻的互联中心点在参数空间的分布,很明显两个编队航迹起始成功。
图8所示为两个编队的航迹起始图,从图中可以看出,同一编队中的目标量测点迹相互交叉,没有固定的相对位置。该航迹起始过程可以满足编队起始的需要,能够较精确的完成编队目标的起始。
由以上分析,K-均值聚类算法与Hough变换的相互结合给编队目标航迹起始和目标跟踪提出了新的思想。前者通过聚类更加准确的求出了子群的中心,为后者Hough变换准确判断子群中心点是否在一条直线上提供了更好的条件。总的来说,该方法思路清晰,计算量较小,去除杂波能力强,航迹起始率高。
6 结束语
本文提出了一种编队目标航迹起始算法,用于密集杂波环境下编队目标航迹起始分析。
该算法将聚类算法和Hough变换思想引入到编队目标航迹起始模型中,本文算法不仅能在密集杂波环境下对目标有效航迹起始,而且航迹起始时间短,航迹起始成功率高,节省了雷达资源,满足了现代战场环境下的战争需要。
但同时,当一个编队中目标成员个数较少时,特别是在杂波特别密集时,杂波和目标形成的聚类就会对子群中心的求取产生较大的影响,Hough变换的效果和正确率还有待于进一步提高。因此,如何降低杂波对稀疏编队航迹起始的影响,是下一步工作的重点。
[1]潘泉,梁彦,杨峰,等.现代目标跟踪与信息融合[M].北京∶国防工业出版社,2009∶89-92.
[2]SOFIKNE AFFES,SAEED GAZOR,YVES GRENIER.An algorithm for multisource beamforming and multitarget tracking[J].IEEE,1995,98(12)∶57-61.
[3]SALMOND D J,GORDON N J.Group tracking with limited sensor resolution and finite field of view[J].Signal and Data Processing of Small Traget,2000,57(45)∶45-48
[4]何友,修建娟,张晶炜.雷达数据处理及应用[M].2版.北京∶电子工业出版社,2009∶184-185.
[5]金术玲,梁彦,王曾福,等.两级Hough变换航迹起始算法[J].电子学报,2008,26(3)∶234-237.
[6]KEVIN GILHOLM,SIMON GODSILL,SIMON MASKELL,et al.Poisson models for extended target and group tracking[J].Signal and Data Processing of Small Traget,2005,34(78)∶67-71.
[7]时银水,姬红兵,汤金平.对断续点迹的速度模糊聚类航迹起始研究[J].仪器仪表学报,2009,10(30)∶38-42.
[8]耿文东.编队目标跟踪综述[C]//第十届全国雷达学术年会.北京∶国防工业出版社,2008∶367-371.
[9]YANG CHEN-YANG,QU JIAN-MING,MAO SHI-YI,et al.An initialization method for group tracking[J].IEEE,Signal and Data Processing of Small Traget,1995,45(60)∶303-306.
[10]SERGIOS THEODORIDIS,KONSTANTINOS KOUTROUMBAS.Pattern Recognition[M].李晶皎,王爱侠,张广渊,译.北京∶电子工业出版社,2006∶317-318,410-412.
[11]蔡慧,刘洪波,韩国栋.基于K均值聚类的随机网络拓扑模型[J].计算机工程与设计,2009,30(5)∶1089-1090.
[12]王峰.基于Hough变换的航迹起始算法[J].杭州电子科技大学学报,2008,28(6)∶87-90.
