自动切割机图像自动对焦
2010-03-23高金龙周建生
高金龙,张 菊,高 阳,周建生
(北京中电科电子装备有限公司,北京 100176)
切割机由传统机型发展到全自动切割,增加了图像智能模块,突破了自动对焦的技术难题。自动对焦即切割机系统能够通过自动寻找基准图像在全片图像中的匹配位置,通过控制电机找到合适的位置,全自动进行划切,无需人的参与。而焦距对焦则是图像清晰度算子。由电荷耦合器件(CCD)在不同焦距的位置采集图像,分析计算出相应图像的清晰度值,进而在合适清晰度值的位置进行子图像的准确匹配对焦。仿真图如图1所示。虽然目前流行了多种图像清晰度算法,但是还没有权威机构给出计算图像清晰度的统一标准,这是因为针对不同应用环境,不同的算法都有着各自的优点。本文结合全自动切割机,分析不同算法的原理与实现,并且在实际中进行了测试,最后给出了在全自动切割机中比较合适的应用算法。

图1 自动对焦系统框图
1 图像显示的视觉误差存在性
CCD对图像进行采样结束后,要显示在显示设备上,而一般的显示设备为了显示出图像的平坦化(即相邻像素之间能否很好地拼配贴合),不会将相邻像素的距离放得很远,使得在显示过程中,相邻像素之间的亮度相互影响,实现图像的平坦化。
假设图像的点亮度服从二维正态分布:

其中p(x,y)表示点亮度分布函数σ2、u分别表示亮度函数的方差和期望。由于高斯点只有在离中心大约半径2倍以外才能降到峰值的1%以下,参考众多资料,选取距离中心点j(d表示距离点光源中心的距离)以内的点做亮度影响分析。即每一个像素点以自身为中心的十字架上的4个像素点的亮度的影响,进而造成视觉误差,此视觉误差特别表现在像素值高的点向像素值低的点过渡过程或者是像素值低的点向像素值高的点过渡的过程中,视觉误差的梯度变化较大,使得本来的梯度值变小。反而在相对平滑区域的梯度之间相互影响较小,视觉梯度误差变化较小,可能使得会接近于本来梯度大的区域。特别对于明暗相间型的图形,如图2所示。

图2 竖线间隔图案
图中白点表示亮度为1的点,而黑点表示2倍于白点亮度的点。以中心点为原点,建立坐标轴,求出中心点的亮度值。用D表示亮度值,则中心点的亮度值D(0,0):

p1(d)为相邻两个白点在原点(0,0)点的亮度值,p2(d)为黑点在原点(0,0)的值。由于黑点的亮度为白点的2倍,所以上式可以近似的表示为:


求出4个点区域贡献的亮度为:
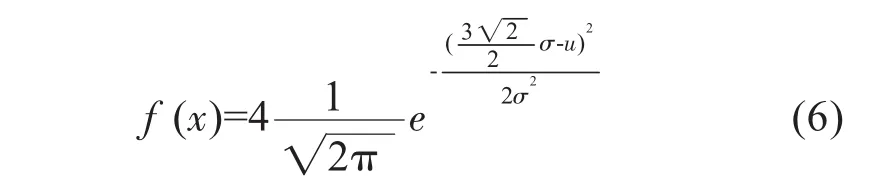
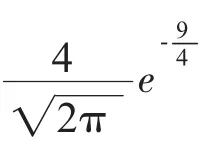
2 图像清晰度评价函数
图像的清晰度不高表现就是图像模糊,由于图像可以看做是在平面内的连续二维函数,所以可以将图像在时域和频域进行分析。在频域,高频部分被削弱,图像看起来就会模糊,反映在时域中就是图像的边缘过渡部分变得平滑,即在图像的边缘部分信息量比较少。
2.1 梯度函数算法
在数学领域中,函数的积分会加强函数的光滑程度,相反函数的微分则表现为函数变得层次分明。由于图像可以看做是在平面内的二维离散函数,所以可以用微分尖锐化来评估一幅图像的清晰度,最常用的微分尖锐化处理方法为梯度处理法。即如果一幅图像的边缘表现的层次感较强(尖锐)越清晰,则其梯度值越大,反之也成立。
采用拉普拉斯算子对图像进行处理,算子的各个系数为 4,-1,-1,-1,-1,如图 3。
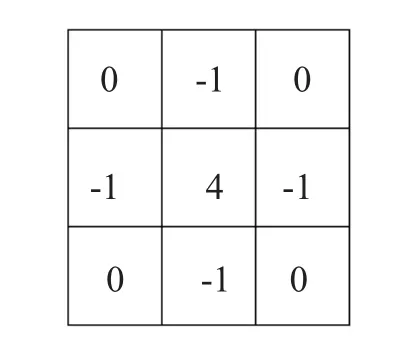
图3 拉普拉斯变换算子
用下面公式计算清晰度:

P(x,y)代表点(x,y)的梯度,f(x,y)为该点的像素值。求得p值后,需要将其做一定的处理,本文采取的是将p除以被计算到的像素的点数(这里消除了最外的一个像素圈)作为清晰度评价的算子。在图像的边缘处,p的值将会比其余平缓变化区域的值大,如果这样的p值越大,即整个图像的边缘信息较多,纹理明显,图像清晰度越高。
2.2 傅里叶变换算法
在频域的范围内,图像的处理分为高频部分、低频部分和直流部分,与时域向对应的分别是图像细节突出的部分、图像模糊的部分和图像背景不变的部分。如果一幅图像是清晰的,那么它应该包含有更多的细节部分和边缘变化明显的部分,即频域中的高频部分比较突出,反之,一幅模糊的图像在低频部分占据的比例更大一些。将一幅图像离散化。并用下面的公式进行图像的傅里叶变换。G(m,n)代表点(m,n)时域的像素值为g(i,k)的频域值。采用碟形算法计算出一幅图像的傅里叶变换是:N必须是2的整数倍n,因此,图像就被切除了大于n小于图像行或者列像素数的那部分。G(m,n)要经过相应的处理,将计算得到的高像素的点占据整个处理像素点的占空比作为清晰度评价算子。

2.3 小波变换算法
由傅里叶光学理论知,CCD镜头系统等价于一个低通滤波器,聚焦越准确,截止频率越高,聚焦越散焦,截止频率越低。从时域讲,点光源成像之后成为有一定大小的像斑,相同领域像素相互影响,在频域,高频分量的流失造成图像的细节模糊。基于此,小波变换可以用一组正交基,将图像变换在不同频率的分量上。如图4所示。
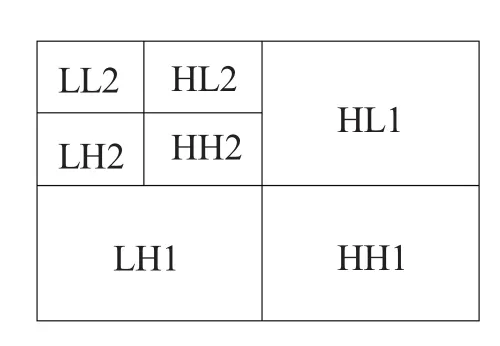
图4 小波变换频域分布图
H代表高频能量,L代表低频能量,HLi代表第i次小波变化后的高频中相对低频部分的能量。将图像离散化后,用下面的计算式进行计算:

φi代表一组小波基代表第i次小波变换的第部分能量。在小波变换完成后,用来作为图像清晰度算子,值越大,即高频部分占据的能量越多,则图像越清晰,反之图像将更模糊。
2.4 熵变换算法
图像的熵值是衡量信息丰富程度的一个重要指标,表示了偏离直方图高峰灰度区的大小,清晰图像的熵大于模糊图像的熵,根据香浓信息理论,熵最大时信息量最大,如果图像中所有灰度级出现概率趋于相等,则包含的信息量趋于最大。用下面的公式计算图像清晰度:
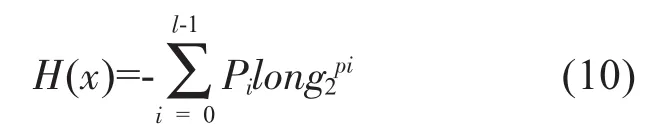
pi为图像灰度值的概率,l为灰度级总数。H(x)越大,则图像的清晰度越高,反之也成立。
3 算法的测试数据与比评价
3.1 测试数据
在自动切割机上在相同光照下不同焦距的截图如图5所示。

图5 清晰图、模糊图和清晰图的噪声图
用4种不同的清晰度算子测量出来的数值如表1。

表1 测试数据
3.2 算法评价
对一幅图像不同清晰度值的合理性选择用差值的扩分来衡量。即从意图纯黑的图像逐行或者逐列一次一次的加工像素的值,从模糊图像到清晰图像需要进行的改变次数在整个改变过程中的相对快慢,例如对于梯度算法,可以用(54.18450-35.32217)/54=0.3493,即从纯黑到相应图的过程中,在细节部分花费的时间在整个过程中占到34.93%。如表1所示。从表中可以看出,小波变换算法的数值最高,而梯度算法最低。
从算法复杂度来分析,梯度算法在取得每个像素值的过程中,用了2次循环,其余的都为线性操作,故时间复杂度为O(n2)+O(1)=O(n2),空间复杂度为O(1)。而傅里叶算法中,主要的时间花在碟形算法中,其时间复杂度为O(n3)。在计算碟形算法的时候,动态的申请了O(length*height)个空间,所以空间复杂度为O(length*height)。小波变换时也只是在取像素的时候用到了O(n2)的时间复杂度,需要申请2个临时的空间,所以空间复杂度也为O(length*height)。熵编码只是各点像素的能量和概率,时间复杂度为取到像素点,只用到一次循环,时间复杂度为O(n2),空间复杂度为O(1)。通过上述的比较,傅里叶算法时间复杂度和空间复杂度最高,运算速度最慢。熵编码变换算法的时间复杂度和空间复杂度最小。运算速度最快。
在自动切割机中,聚集了大量的电子元件,其产生的电信号和磁信号,对CCD产生的噪声影响很大,所以在算法处理的过程中,噪声处理占据了很重要的一部分。通过人为的加入噪声后,在测量其中的清晰度在表1中显示。从表中可以看出,小波变换算法和熵变换算法对随机噪声的敏感程度太大,以至于在变换过程中已经不受控制。只有傅里叶变换算法和梯度变换算法保持正确的趋势。
小波变换算法之所以不能够灵敏的反映出加入噪声后,图像清晰度变化的趋势,是因为小波变换采用一组基于正交的小波,在局部范围内进行变换,而算子噪声的随机性,造成了在高频部分和低频部分的不均匀分布,使得高频分量的能量和低频分量的能量不能正确的代表源图像的信息,所以出现了偏差。然而用熵变换编码过程中,由于在一幅图像的熵代表的是该幅图像的所含信息丰富程度的指标,加入噪声后,不同像素值的噪声出现的概率是一个随机事件,造成了清晰图像的灰度直方图的紊乱,整个图像的灰度概率不再区域均匀分布,故熵的值将会变小。
通过上述各技术指标,在自动切割机上采用梯度算法比较合适,在计算速度较快的工控机上也可以采用傅里叶变换算法。
4 结论
(1)为了全自动切割机能够准确地实现图像的自动对焦,必需要有适合全自动切割机工作环境的清晰度算子。即要考虑全自动切割机的工控机计算速度以及电流或者是磁性造成的噪声影响等。
(2)在实施不同算法的变换过程中,对灰度图像的每个像素点实施算法改变灰度值的时候,虽然灰度图像显示的规定灰度值在之间,但是不能将大于255的像素值直接赋值为255。通过程序的执行可以发现,一个超过255的像素点,并没有在执行过程中出现溢出现象,进一步试验表明,超过255的像素点采用的是对255取余数操作后的显示。
[1]Kenneth R.Castler著,徐光祐译.Digital Image Processing[M]北京:电子工业出版社出版社,2000.
[2]徐慧.Visual C++数字图像使用工程案例精选[M].北京:人民邮电出版社,2004.
[3]陈兵旗,孙明.Visual C++实用图像处理专业教程[M].北京:清华大学出版社,2004,3.
[4]张龙潇,王沁磊.Vsual C++6.0应用与提高[M].北京:科学出版社,1999,1.
[5]刘兴宝,袁道成.基于纹理分析的小波变换图像清晰度评价方法研究[J],仪器仪表学报,2007,28(8):1508~1512.
[6]廖绮绮,李翠华.基于支持向量机语义分类的两种图像检索方法[J].厦门大学学报,2010,49(4),487~494.
