采用图分解的特征识别算法研究
2010-03-21刘晓平
刘晓平, 吴 敏, 金 灿
(合肥工业大学计算机与信息学院,安徽 合肥 230009)
CAD/CAE/CAM从现代工业体系来看是一个密不可分的整体。CAD用于产品的设计,CAE对CAD设计的产品进行优化,CAM根据CAE优化的结果进行制造。其中,CAD是基础,CAE是保障,CAM是应用,三者密不可分。尤其是CAD跟CAE联系相当紧密。但是,由CAD建造的模型往往不能够直接用来进行CAE分析,这是由于CAD建造的模型存在一些诸如细小特征和高曲率特征一类的复杂特征,会显著增加网格划分的单元数量,从而消耗大量的计算资源,甚至导致计算结果出错。在这些复杂特征中,有些特征的存在与否对计算结果影响不大,因此在CAE分析之前,如果识别出CAD模型中的细小特征和高曲率特征,分析这些特征的删除或替换对计算结果的影响程度,生成一个模型的对应误差程度的若干模型态[1],并依此制定特征抑制方案,就可以大量节省计算资源,有效提高计算效率。而特征识别技术是一切工作的技术基础。
自动特征识别技术从上个世纪80年代首次提出[2],至今已取得了很大的成果。基于图的特征识别方法是目前主要的特征识别方法之一,它通过图结构来描述特征的几何及拓扑信息,并在零件的图结构中搜索匹配特征子图来达到识别特征的目的。文献[3]提出了一种基于图的特征识别方法,用包含相关拓扑和几何属性的面边邻接图表示用户定义特征,再在对应的零件邻接图中搜索相似子图。该方法虽然克服了基于图的特征识别不擅长处理相交特征的弱点,提出了虚相交及多属性的方法,解决了一些相交特征的识别。文献[4]结合基于痕迹的和基于图的特征识别方法,先对属性邻接图进行分解,再将特征图与每个子图进行匹配,可以有效地降低子图匹配的算法复杂度。但是,目前主流的特征识别算法识别出的特征多由面集表示,抑制操作复杂度高。如果以三维实体来表示特征,则可以大大地方便特征的删除和替换。同时,在面向分析的特征识别中关注的是如何将模型分解为最简单元,尽量保证同一单元具有相近的网格划分属性,如网格直径等,以方便衡量计算误差和计算时间。因此,如何可以更好地将模型分解为最简单元,是CAD/CAE集成系统中特征识别的关键问题。
本文提出基于属性邻接图分解的方法实现特征识别,以完成对模型的分解。该方法不再局限于特征类型,只要合理控制顶点的可分解性判断则可以得到期望的模型分解结果。同时该方法可以将特征识别为实体,方便了特征删除和替换操作,以完成模型的简化。
1 图分解准则
1.1 相关定义
定义1特征是模型分解之后的最小单元,其满足以下条件之一:
(1)体积小于一定的阈值;
(2)包含曲率大于一定阈值的曲面。
定义2若面f1和f2具有相同曲面方程,但是被划分为不相邻的部分,则称f1和f2为Co-defined面[3]。
如图1所示,其中面F1、F1′为Co-defined面。
定义3在模型的属性邻接图分解之后,如果有些面所对应的顶点存在于两个或两个以上的连通分量中,这样的面称为特征分解面。
定义4对于属性邻接图中顶点v及其相邻的所有顶点集合V_adjacent,v与集合V_adjacent中每个顶点对应的曲面方程的交线集合V_curves。按照邻接顺序将曲线之间求交点,若这些曲线首尾相连,则称这些曲线集合为环。
基于上述定义,如果一个顶点有两个或两个以上的环,那么该顶点所对应的面为特征分解面,该顶点为可分解顶点。本文提出的基于图分解的特征识别算法均基于此前提。
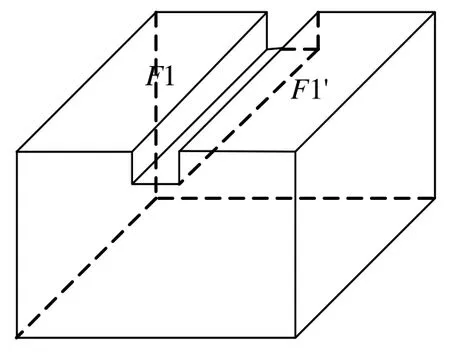
图1 Co-defined面
1.2 属性邻接图(AAG)
要进行特征识别,首先要根据将B-Rep表示的三维模型形成面边邻接图,其中模型的面对应图中的节点,边对应图中的弧。在面边邻接图的基础上,将模型的几何或拓扑属性添加到相应的弧和顶点上,则形成属性邻接图,如图2所示。

图2 属性邻接图
为了方便顶点的可分解性判断及体特征生成,在AAG中添加以下属性。
(1)弧的属性
· 所对应边的几何信息,包括边的端点及相应曲线方程,用于分解之后连通分量生成体特征。
· 边的凹凸性,用于辅助判断边所在的面的外法向,其判断方法参考文献[5]。
(2)顶点的属性
· 所对应面的几何信息,即面的方程,用于分解之后连通分量生成体特征。
· 所对应面的环的数目,以判断顶点是否可以分解。
· 所对应面包含的环的集合,在图分解时作为依据,根据环的具体情况确定顶点复制数目并完成弧的连接。
· 分解方向,即未分解(0)、正向(1)、负向(-1)。如果某顶点还没有分解,或者不能够被分解则记为未分解(0);如果分解之后,该顶点的拷贝对象对应的环为内环,则记为负向(-1),表示该顶点所相连的面的原法向需要修改;否则记为正向(1),表示面的原法向不必修改。
2 基于图分解的特征识别算法
2.1 算法流程
基于图分解的特征识别算法流程为:根据顶点分解准则对属性邻接图进行分解,以完成模型的分解。其步骤如下:
Step 1化简初始属性邻接图,合并其中Co-defined Faces顶点;
Step 2对化简后的属性邻接图,判断每个顶点是否可分解,若可分解则按照分解规则分解每个顶点;
Step 3当所有顶点都分解之后,判断最终属性邻接图包含连通分量的数量,将每个连通分量生成体单元,对于每个体单元根据设置的特征阈值判断其是否为特征。
下面将对这3个步骤分开详细阐述。
2.2 属性邻接图的化简
在模型中,有些面具有相同的几何方程,但被特征划分为不相连的几个部分,因此具有不同的拓扑结构,即 Co-defined 面。在对属性邻接图进行分解之前,需要将Co-defined面对应的顶点合并。
合并步骤如下:
Step 1找出Co-defined面集合FS;
Step 2对集合FS中的每个面,找出其在面边邻接图中的顶点,在其与原图中其余顶点邻接点之间添加一条边,再删除其余顶点。图3为图1中的槽特征中的Co-defined面处理前后的属性邻接图对比。

图3 Co-defined面顶点合并
2.3 顶点可分解性判断及分解
对于每一顶点v按照以下步骤执行:
Step 1求该顶点所包含的环:
(1)对于顶点v,获得其相邻顶点集合V_adjacent;
(2)根据邻接信息查找V_adjacent集合中的所包含的环,并记录环及环的数目。
Step 2若环的数目大于1,且存在内环,则执行Step 3,否则结束;
Step 3根据环分解顶点:
(1)将顶点v复制m份添加到属性邻接图中,其中m为顶点v所包含的环的数目;
(2)对于v所包含的每一个环,分配一个v的拷贝v′,并将L中边所对应的弧原先指向顶点v的改为指向v′;
(3)删除顶点v。
在对属性邻接图中每一定点v执行以上操作后,在将属性邻接图划分为若干个子连通分量,如图4所示,是对图3中化简之后的槽的属性邻接图顶点分解之后的结果。
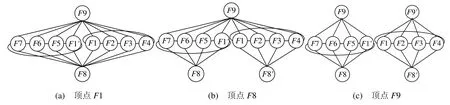
图4 顶点分解示意
2.4 体特征的生成算法
完成属性邻接图的分解之后,获得了对应每一单元的属性邻接图,在此基础上生成对应的体特征。文献[6]中提出通过面延伸生成体特征方法,但是只处理了特征表面为平面的情况,没有涉及面与面之间的邻接关系。这里根据属性邻接图,利用面的邻接关系,通过延伸必要的面生成体,再根据设定的阈值判断所生成的体是否为特征。对于分解之后的属性邻接图中的每个连通分量进行以下操作:
Step 1找出属性邻接图中分解生成的所有顶点,对其中的每个顶点v,修改其所对应的曲面的边界。
Step 2确定每个面的方向。
Step 3根据已有的点、线、面生成Brep表示的三维模型。
Step 4判断所生成的体是否满足特征的条件(体积阈值和曲率阈值);若满足作为特征。
3 实 例
如图5所示,本节以文献[7]中给出的计算LOD的模型为例。针对此种模型可分解为13个最简单元,其中特征1~8(小圆柱)满足特征条件(1)、体积很小;特征9(中间圆孔)满足特征条件(2)包含高曲率曲面。模型中其他部分保存在基座中。由于特征识别的目的是为了替换,程序中仅仅是将最后生成的体特征保存,作为模型的属性,并没有显示出来。
4 结 束 语
针对CAD/CAE模型转换与CAD/CAM转换的区别,提出了基于图分解的特征识别算法。依据顶点分解准则,判断顶点的可分解性,并对属性邻接图进行分解,再针对分解之后的属性邻接图中的每个连通分量生成体特征。该算法不局限于特征类型,可以识别出常见的加工特征,如槽、孔等,只要合理控制顶点的可分解性判断则可以得到期望的模型分解结果,识别出更多的特征。同时该方法识别出的为体特征,与用面集表示的特征相比,在特征抑制时,可以在特征这一较高层次[6]上方便地进行特征删除和替换以完成模型的简化。
该方法依然存在一些问题,如属性邻接图到体映射存在一定的不确定性。同时,对于相交特征的分解进行更深入的思考是下一步工作的目标。

图5 实例
[1]刘晓平, 金 灿, 李书杰. 有限元仿真软件中建模的多态机理研究[J]. 系统仿真学报, 2007, 19(3):538-542.
[2]Corney J, Hayes C, Sundararajan V, et al. The CAD/CAM interface: a 25-year retrospective [J].Journal of Computing and Information Science in Engineering (Transactions of the ASME), 2005, 5(33):188-197.
[3]Venkataraman S, Sohoni M, Kulkarni V. A graphbased framework for feature recognition[C]//6th ACM Symposium on Solid Modeling and Applications, 2001:194-205.
[4]Rahmani K, Arezoo B. A hybrid hint-based and graph-based framework for recognition of interacting milling features [J]. Computers in Industry, 2007, 58:44, 304-312.
[5]周 炜. 基于图的边界模型的加工特征识别技术[D].南京: 南京航空航天大学, 2006.
[6]Dong X, Wozny M. A method for generating volumetric features from surface features [J].International Journal of Computational Geometry &Applications, 1991, 1(3): 281-297.
[7]Lee Sang Hun. Feature-based multi-resolution modeling of solids [J]. ACM Trans. on Graphics, 2005, 24(4):1417-1441.
