GIS环境下缓和曲线绘制方法研究

王明生， 闫小勇

（石家庄铁道学院交通工程分院，河北 石家庄 050043）

交通地理信息系统（Geographic Information System for Transportation，GIS-T）是收集、存储、分析和传输关于交通系统及其相互影响区域的特定类型信息的地理信息系统，其主要功能是对公路、铁路等线性交通实体进行建模与分析，建立表达交通线路的数据模型是GIS-T研究的核心内容[1]。交通线路是一类典型的人工构筑物，其线路中线在平面上由直线、圆曲线和缓和曲线按一定规则组合而成[2]。现有的大多数GIS都能够直接绘制直线和圆曲线对象，但没有提供专门的缓和曲线绘制方法。针对这一问题，本文对GIS环境下缓和曲线的绘制方法进行研究，用折线拟合的方法实现缓和曲线对象的准确绘制，并给出缓和曲线上任意点坐标与里程的精确转换方法。

1 GIS中缓和曲线绘制的理论依据

缓和曲线是交通线路中线上连接直线和圆曲线，曲率半径从无穷大逐渐过渡到圆曲线半径R的过渡曲线。交通线路中常用的缓和曲线是回旋线，其基本特征是曲线上任一点的曲率半径和该点距曲线起点弧长的乘积为一常数。根据这一几何特征，可以建立缓和曲线的数学模型[2]。若以缓和曲线起点为坐标原点，起点处切线方向为x轴，法线方向为y轴建立直角坐标系，则缓和曲线可用如下参数方程描述

从缓和曲线的数学描述模型可以看出，缓和曲线是复杂的高次连续曲线。而计算机是离散化的数据处理系统，由计算机图形学的基本原理可知，在数字计算机中任意空间曲线都是用多条直线段（即折线）来近似表示的[3]。其一般过程是在曲线上提取若干样本点，用直线段进行连接，创建接近曲线形状的折线。用折线近似表示曲线的几何意义就是分段用弦替代弧，由于弦长只有在微分线段的情况下才与弧长相等，因此用折线拟合曲线不可避免地存在误差，但可以通过增加分段数量使误差降低到可接受的范围之内[4]。由于GIS将折线作为描述空间线状实体的基本矢量模型，其他空间曲线对象都用折线近似描述，因此在GIS中用折线拟合的方法绘制缓和曲线是可行的。关键是要确定合理的分段数量，使之既能满足精度要求，又不至于因为分段过多而对数据管理和分析带来困难。

2 折线拟合缓和曲线分段数的确定

考虑式（1）中的缓和曲线参数方程，由于该方程中积分的原函数无法用初等函数表示，可以运用数值积分方法对其进行求解。在这里采用复化梯形公式[5]求解该积分，有

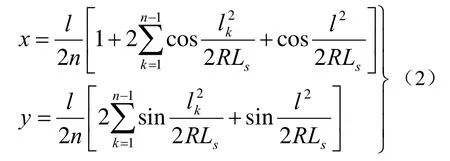
复化梯形公式的几何意义就是用折线分段逼近曲线，其中n为分段数量。如果能够选定合适的分段数n，使式（2）的计算结果满足坐标计算精度要求，那么用n段折线近似表达缓和曲线就能满足精度要求[6]。下面根据数值积分中的误差理论[5-6]，推导分段数n的计算公式。

用式（2）代替式（1）产生的截断误差是

要保证缓和曲线的绘制精度，必须使截断误差小于一定值ε，即

根据式（3）和式（4），有

其中

由于ξ∈[0,l]，而l∈[0,Ls]，故

将式（7）代入式（5）中，可以得到分段数n的计算公式

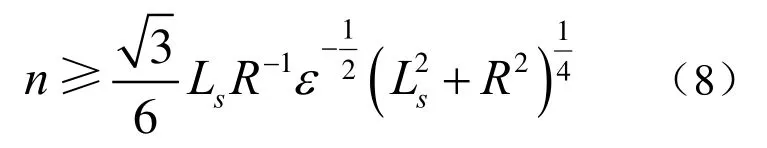
分析式（8）可以看出：用缓和曲线的分段数n与ε成正比，若精度提高一个数量级，则n值增大约3.3倍；同时，缓和曲线长度越长，终点曲率半径越小，则需要的分段数也越多。

表1列出了在不同精度要求下，几种典型缓和曲线长和终点曲率半径组合条件下分段数n的计算值。为验证计算精度，表1中同时列出了拟合后的折线段长度（取6位小数）。可以看出，根据式（8）计算出的n值，能够非常精确地用折线拟合缓和曲线。

表1 不同条件组合下分段数n及折线长度计算值

3 折线节点处的坐标计算

对于任意一条缓和曲线，在给定缓和曲线长度和终点曲率半径后，就可根据式（8）确定拟合折线的分段数。下一步的工作是计算拟合折线各节点处的坐标，然后用直线依次连接这些节点就可绘制一条缓和曲线。

根据式（1），折线上第i个节点的坐标可以用下式计算

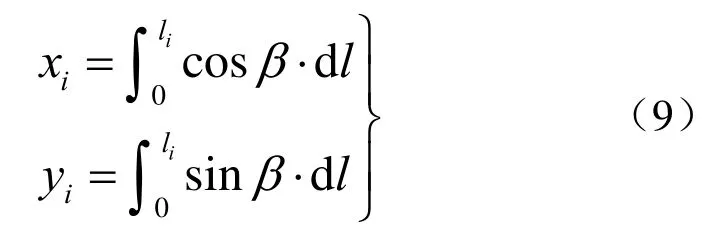
积分时需将式（9）中的三角函数展开为有限项麦克劳林级数

在用式（10）计算各点坐标时，为确保所绘制缓和曲线的精度符合要求，节点坐标计算精度一般应比曲线拟合精度高出1倍以上[6]，这就对式中的级数展开项数提出较高的要求。一般文献建议的只展开到第2～3项是远远不够的[7-8]，当缓和曲线曲率半径较小时将会产生较大误差，应采用严密的数学方法确定各点坐标计算时级数展开的项数[9]。

上述坐标计算是在缓和曲线的局部坐标系中进行的，实际应用时还要根据缓和曲线起点处的大地坐标、方位角等将各点坐标转换为大地坐标[2]。此外，实际的交通线路中还存在一类特殊的缓和曲线——部分缓和曲线。部分缓和曲线连接两个圆曲线，不能直接用本文中的方法计算坐标，需要用还原方法先将部分缓和曲线恢复成完整缓和曲线[10]，再进行折线拟合和坐标计算。

4 缓和曲线任意点坐标与里程的相互转换

通过前述过程，可以在GIS中实现缓和曲线对象的准确绘制。但对基于GIS的交通线路设计等应用系统[11]来说，不仅要求能够绘制缓和曲线图形，还要求能够实现曲线上任意点里程（为描述简便起见，此处的里程定义为缓和曲线上任一点距起点处的弧长）与坐标之间的准确转换。根据缓和曲线任意点里程计算坐标的方法比较简单，直接利用式（10）即可完成。本节重点讨论根据点坐标计算里程的方法。

给定缓和曲线上任意一点P的坐标求其里程，最简单的方法是以一定的步长从起点开始依次计算每一步长点的坐标，和点P坐标进行比对，但这种方法是一种蛮力法，效率较低。本文给出一种效率更高的二分比对算法，其基本思路是在不断二分缓和曲线弧段的过程中，比较二分点M和P点之间距缓和曲线起点S的距离差，如果此差值缩小到允许误差之内，则可以认为用M点的里程代替P点的里程符合精度要求。算法的具体步骤如下：

（1）初始化。令迭代算子k=1；输入最大允许误差ε，缓和曲线长度L，起点S的坐标xs,ys和欲求里程的P点坐标xp,yp；计算P点与S点之间的距离令二分点M的里程初始值

（2）根据当前M点的里程值用式（10）计算M点坐标再计算M点与S点之间的距离

（5）令迭代算子k=k+1，转第（2）步。

上述算法的迭代次数与缓和曲线长度L及最大允许误差ε有关，最不利的情况下，迭代次数例如，当L=1000 m、ε=0.001时，最多迭代20次就可以计算任意给定点处的里程值，效率可以满足实际应用的要求。

5 结 束 语

本文从分析缓和曲线几何特征和数学模型出发，借鉴计算机图形学中曲线逼近的思想，用折线拟合的方法实现了GIS环境下缓和曲线对象的准确绘制。基于数值积分的复化梯形公式，推导出了缓和曲线拟合折线分段数计算的严密数学公式。进一步给出了缓和曲线上任意点坐标与里程的精确转换方法，使研究成果更具实用性。上述方法已采用SuperMap GIS软件提供的二次开发平台SuperMap Objects实现。经实际使用，在绘图精度和计算效率等方面能够满足复杂应用的需求，可适用于交通线路设计、移动设施定位等对线路里程、事件点坐标精度有较高要求的GIS-T应用系统。

本文提出的方法对于在AutoCAD等软件环境中绘制缓和曲线对象同样适用[12]，但在GIS环境中用折线拟合方法绘制缓和曲线对象更具优势。因为折线是GIS的基本矢量对象，用折线拟合的缓和曲线不用进行任何特殊处理，就具备各类空间分析与空间关系运算功能，而这些功能在CAD环境中是较难实现的。

当然，用折线拟合缓和曲线也存在曲线外观光滑性较差的缺陷，特别是当放大显示缓和曲线的细节特征时，虽然各点位坐标精度依然能满足要求，但曲线的外观可视化效果不佳。可以采用增加拟合点的方法对曲线进行进一步平滑，但由此也会带来绘图效率下降、数据存储量增加等问题。在GIS环境中如何改善缓和曲线外观可视化效果，还需要进行更深入的研究。

[1]MILLER H J, SHAW S L. Geographic information systems for transportation: principles and applications [M].Oxford: Oxford University Press, 2001. 11-57.

[2]詹振炎. 铁路选线设计的现代理论和方法[M]. 北京:中国铁道出版社, 2001. 47-51.

[3]魏海涛. 计算机图形学[M]. 北京: 电子工业出版社,2001. 1-8.

[4]郭仁忠. 空间分析(第2版)[M]. 北京: 高等教育出版社, 2001. 3-78.

[5]李庆扬, 王能超, 易大义. 数值分析[M]. 武汉: 华中理工大学出版社, 1986. 177-193.

[6]李全信, 叶 刚. 完整和不完整缓和曲线在AutoCAD中的精确表示[J]. 城市勘测, 2007, (1):61-65.

[7]邱荣茂, 王大鸣, 周乔勇. 基于AutoCAD的线路缓和曲线的自动绘制[J]. 工程图学学报, 2005, 26(1):30-34.

[8]符锌砂. 公路计算机辅助设计[M]. 北京: 人民交通出版社, 1998. 91-92.

[9]谯生有. 缓和曲线坐标计算误差分析[J]. 测绘通报,200l, (11): 37-38.

[10]张福荣, 焦广彦. 还原方法计算卵型曲线中间缓和曲线点坐标[J]. 测绘通报, 2004, (1): 38-40.

[11]张晓东, 王明生. AutoCAD环境下的铁路线路平纵横集成交互设计[J]. 工程图学学报, 2006, 27(5):12-15.

[12]王中伟. 道路与匝道中线自动绘制的算法与实现[J].工程图学学报, 2007, 28(1): 144-147.