振动监测与故障诊断技术在“风云二号”扫描辐射计中的应用

张 利，付国庆，梁 伟

（1. 上海交通大学 机械与动力工程学院，上海 200030；2. 上海卫星工程研究所，上海 200240）

0 引言

卫星在轨运行时，往往是转动机械部件最容易出故障。这些部件不允许随便拆装检查，这就要求必须在它们运行时提取故障症状的信息[1]，对其进行在线状态监测和故障诊断，以识别现状并能预测未来。为此，如何在研制过程中结合少量试验和特定的监测方法对卫星转动机械部件的状态进行评价，对其性能变化趋势和寿命极限进行预测和评估等问题已提到议事日程上[2]。

转动部件的状态监测和故障诊断有多种方法，包括振动音响法、速度变化法、声发射法、电流分析法、温度法、压力脉动法等，其中，包括振动音响法和速度变化法的振动诊断技术在被诊断系统的信号采集、数据处理、故障识别和诊断中显示出简便可靠的优越性，尤其适用于不停机在线监测和诊断报警[3]，可从测试活动部件在规定动作过程的自身振动信息中分析出正常、异常或缺陷等。早在 20世纪 70年代初美国就运用此方法对卫星消旋组件进行了振动分析；20世纪80年代在国外已经形成一门新的、融合多项技术的学科——机械故障诊断学；国内于 20世纪 90年代将这项技术用于涡轮发动机、炼油设备、大型电机等设备的分析；由此，国内外繁衍出各类诊断设备及其分析软件。

1 转动机械部件振动故障分析原理及特点

振动信号中有丰富的信息，其中包含故障信息。实际上，机械故障信号通常是非平稳信号，如果背景噪声比较大，则故障信号被隐藏在噪声中。所谓故障的振动诊断技术就是用各类传感器在运行的系统中提取振动信号，并加以分析，将有故障（或怀疑有故障）的监测对象和正常系统的振动特性作比较，以期识别出系统的故障状态。

1.1 时域分析

采集数据是状态监测的第一步，将来自传感器的模拟信号转换成数字信号，生成时域图。典型时域图的长度非常短，往往是ms量级，通常取转轴的 5～7转数据，在时域图上可以看见 5～7个正弦波加上任一变形波形。

时域分析法主要研究平均值、均方值、方差等。被测件处于正常状态下运行时，时域图由大量的、随机的、强度接近的振动信号组成；一旦发生故障，信号中会出现有规则的、周期性脉冲，冲击的量值要比正常状态下大得多。因此，用振动信号诊断设备故障时，首先要在振动信号中找出隐含的周期分量。

1.2 频域分析

振动信号的频域分析法是故障诊断中应用颇广的方法，其中用到最多的方法是傅立叶分析（也称频谱分析或谱分析）。按傅立叶分析原理，0～t时间段内呈周期性或延拓后视为周期性的平稳信号，可分解为许多谐波分量之和，见公式(1)：

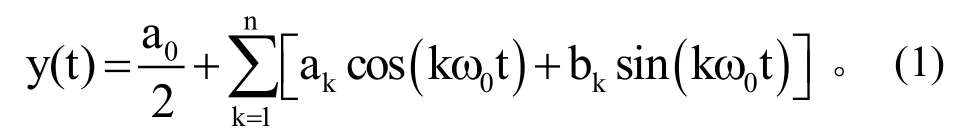
这意味着通过这种变换能将时域信号变成频谱（见图1）。通过振幅和频率（而不是时间），就更能分析振动信号的周期性成分。

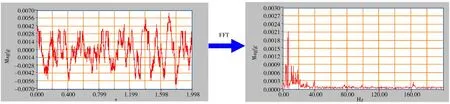
图1 傅立叶转换图Fig. 1 FFT(Fast Fourier Transform Algorithm)

描述转动部件振动的运动学参数有位移、速度、加速度。

转动部件运行矢量的轨迹或位移迹线可简单描述为正弦波形，其方程式为

式中：x为振动任一瞬间的位移，m； A为振幅，m；ω为角频率，rad/s； t为时间，s；φ为振动初始相位，rad。

速度υ是时间的函数，是对位移的一次导数，其数学式表达为

再对速度求导，可得加速度a，其数学表达式为

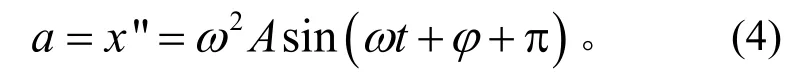
从公式(2)～(4)可以看出[4]：

1）振动位移、速度和加速度信号的频率相同。不管采用何种表示方式，故障性质不会变化，都可以用于振动监测。

2）在相同位移幅值下，频率越高，振动所产生的交变应力越大，对设备的危害越大。因此故障频率越高，位移幅值应该控制得越严格。对于旋转机械而言，转速越高，振动标准越严。

3）振动速度及加速度幅值是振动位移幅值和频率（或频率平方）的乘积，幅值中同时反映了振动频率和位移幅值的影响，比单纯的振动位移幅值更全面。

4）振动加速度超前振动速度相位 90º，振动速度相位又超前位移相位90º。

5）同一种故障在振动位移、速度和加速度频谱中表现出来的故障特征不完全相同。假设某故障振动位移信号频谱如图 2(a)所示，频谱中 10 Hz、20 Hz和50 Hz分量幅值都为10 µm，根据公式(2) (4)可以计算出每一频率分量的速度和加速度幅值，如图 2(b)、(c)所示。比较这 3个图可见，高频分量在振动速度和加速度频谱中得到了明显“放大”，频率越高，速度和加速度频谱中高频分量的“放大”作用越明显。因此对于高频振动故障，为了在故障的早期能够比较明显地反映出振动变化，采用振动速度或加速度监测比较有效。反之，低频分量在位移频谱中也同样地被“放大”。

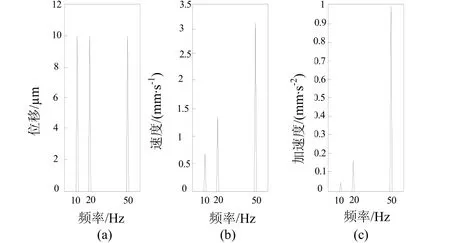
图2 振动位移、速度和加速度频谱比较Fig. 2 Spectrum comparison among vibration displacement, speed and acceleration

6）振动位移、速度和加速度之间可以相互转换。虽然将位移信号对时间求导可以得到速度信号和加速度信号，但是由于求导过程中误差有可能会放大，所以实际上很少进行这样的转换。信号积分过程中的误差是收敛的，因此目前采用比较多的方法是由加速度或速度信号积分求出位移信号。一些采用加速度传感器的振动仪表具有积分功能，可同时显示出振动加速度、速度和位移值。

从振动测量的角度来看，测量振动加速度和位移比较容易实现，而振动速度一般都是通过测量加速度再进行积分后得到，因此，振动检测一般选用位移传感器和加速度传感器。由于位移传感器的安装和测量存在诸多局限，如：需要根据被测产品具体情况设计专门工装；飞轮等部件的转子装在密封的壳体内，无法采用非接触式的位移传感器进行测量；不太适用于高频振动的测量等等，因此，配备高精度高灵敏度的加速度传感器也是必需的。

2 在“风云二号”卫星扫描辐射计状态监测中的应用

“风云二号”卫星扫描辐射计的扫描螺旋副是一种精密小螺距的滑动丝杆副结构，正常扫描频率由北向南是 66.67 Hz、由南向北是 200 Hz。在轨工作时，随着扫描步进的运动，存贮在螺母中的润滑膏被带走，较难得到及时补充。长期这样运行，螺旋副将处于不良的润滑状态，从而使卫星难以达到长寿命高可靠的设计目标。在后续卫星的研制过程中，除了在设计上采取了一系列改进措施外，重点加强了产品的系统级地面试验和全过程性能检测及质量控制，其中，首次尝试性地应用了振动诊断测试分析技术，针对扫描机构在不同输入电压下的振动响应特征以及频谱特性进行测试分析，进而研究失步现象的临界电压和失步状态的时域及频谱特征。

由于其特征频率均大于50 Hz，根据图2可以看出，测量加速度比较合适。

2.1 正常工作时的状态监测

在扫描辐射计工作过程中，对其振动响应进行了全程监测记录，如图3～图7所示。

图3 电机正常工作状态下慢扫的时域响应图Fig. 3 Slow scan time domain response of the motor during normal working condition

图4 电机正常工作状态下慢扫的频谱图Fig. 4 Slow scan frequency response of the motor during normal working condition

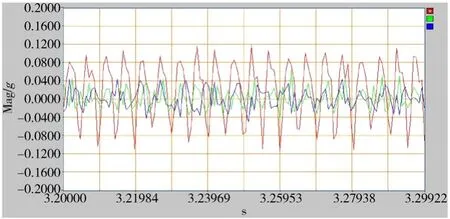
图5 电机正常工作状态下快扫的时域响应图Fig. 5 Quick scan time domain response of the motor during normalworking condition

图6 电机正常工作状态下快扫的频谱图Fig. 6 Quick scan frequency response of the motor during normal working condition

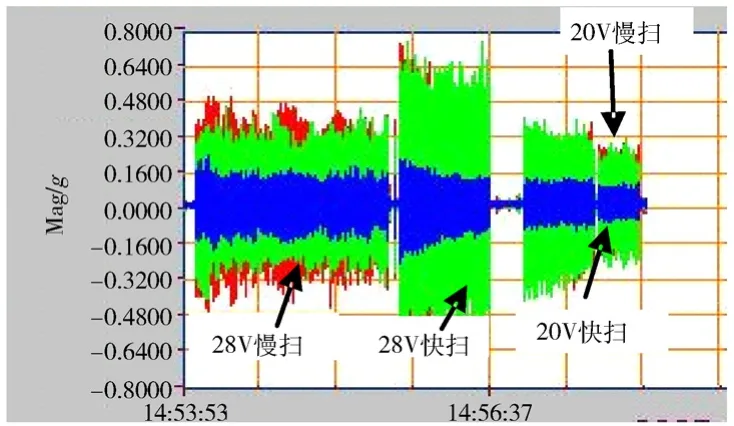
图7 扫描机构4种工作状态下的时域响应对比图Fig. 7 Comparison of time domain response among different working conditions for the scanner

从图3～图7可以看出：

1）在电机没有失步的正常工作情况下，随着电压的降低，振动响应幅值逐步降低（从图 7的对比来看，尤其明显）；同电压的情况下，快扫的响应要大于慢扫；

2）电机快扫特征频率 200 Hz及其倍频（见图 6），时域上 5 ms周期间隔明显（见图 5），频域上特征频率突出；电机慢扫特征频率 67 Hz及其倍频，频域上特征频率突出（见图4）。

2.2 故障模拟试验

在辐射计工作稳定后，通过调节电机的供电电压，使其出现故障，测试所得的振动响应如图8～图12所示。

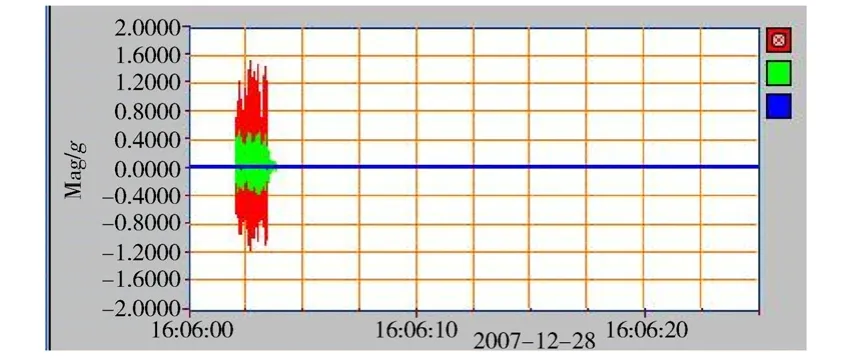
图8 电机在13.5 V快扫状态下的时域响应图（电机失步，响应突然放大为正常值的近10倍）Fig. 8 Time domain response of the motor under 13.5 V quick scan condition

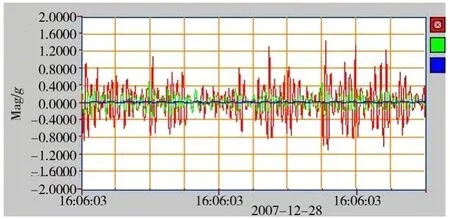
图9 电机失步时域响应细化图（时域上峰值抖动比较严重）Fig. 9 The refinement time domain response of the motor during abnormal working condition

图10 电机失步频谱图（特征频率已经改变）Fig. 10 Frequency response of the motor during abnormal working condition

图11 13.7 V电机濒临失步时域响应图Fig. 11 Verge-of-step time domain response of the motor under 13.7 V scan condition

图12 13.7 V电机濒临失步频谱图（200 Hz特征频率明显，但多出了其0.5X倍频）Fig. 12 Verge-of-step frequency response of the motor under 13.7 V scan condition

从图8～图12可以看出：

1）扫描机构的临界失步电压为13.5 V；

2）在电机没有失步的正常工作状态下，响应普遍较小，而且特征频率明显；但是一旦失步，响应会放大近10倍，而且在频谱上也已经没有了原来的特征频率；

3）在接近失步时（13.7 V），会出现其特征频率的0.5X倍频的明显响应，可以在这一电压附近或者0.5X倍频附近设置预警值。

3 结束语

振动故障诊断技术在卫星地面测试中的应用已得到验证，并取得了较好的效果。

在卫星转动部件的状态监测过程中，要对产品的质量状况给出适当的评价，这就涉及到评判标准问题。标准制定得过高，会造成资源浪费，而标准过低又会影响产品的质量，而且星用转动部件大都是非标产品，各种产品的评价标准不能千篇一律，因此，标准的制定需要大量的数据信息和知识的积累。

虽然振动测量分析在卫星转动部件状态监测和故障诊断的应用方面还有很多问题需要解决和进一步验证，但相信随着相关技术的进步、实践经验的逐步积累以及相关数据库的建立，振动分析技术必将在该领域发挥越来越大的作用，为确保卫星的长寿命和高可靠提供有力保障。

（

）

[1] 张阿舟, 诸德超, 姚起杭, 等. 实用振动工程(3)——振动测量与试验[M]. 北京: 航空工业出版社, 1997: 253

[2] 信太林, 王秀霞. 星用转动部件故障诊断技术探讨[C]∥第六届国际可靠性维修性安全性会议论文集, 2004: 642

[3] 陈长征, 胡立新, 周勃, 等. 设备振动分析与故障诊断技术[M]. 北京: 科学出版社, 2007: 21

[4] 杨建刚. 旋转机械振动分析与工程应用[M]. 北京: 中国电力出版社, 2007: 5