基于Z源的Sepic直流变换器研究
2010-03-19李文燕周永勤姜云峰刁洪君
李文燕,周永勤,姜云峰,刁洪君
(哈尔滨理工大学 电气与电子工程学院,哈尔滨 150040)
0 引 言
目前应用Z源进行直流变换的电路拓扑中大部分都只能实现升压变换功能,对于调压范围比较大的升降压调压电路就无法应用这样的拓扑,为此本文提出一种既能升压也能降压的Z源调压电路拓扑。
传统的Sepic电路能实现升降压功能,而且电源电流和负载电流都是连续的,有利于输入、输出滤波,但它的升压比B=D/(1-D),D为开关的导通比,当D<0.5时实现降压功能,当D>0.5时实现升压功能,而且要实现很高的升压比时,开关的导通比D接近1,这样开关导通时间过长而截止时间过短,会导致损耗和温升过大,影响实用。本文提出的Z源调压电路拓扑实现了升降压功能而且也解决了Sepic电路存在的问题。Z源调压电路的升压比B =D/(1-2D),在D<0.5的情况下能实现Sepic电路的升降压功能,而且当D接近0.5时理论上能得到任意高的输出电压,明显克服了Sepic电路导通比过大的缺陷。
1 Z源调压电路的拓扑结构
Z源调压电路结构见图1,电路由输入电源Ui,二极管D1、D2,Z源网络,开关管Q,电容C1、C2、C3、C0,电感L1、L2、L3和负载R组成,其中Z源网络[1-3]是指由C1、C2、L1和L2连接成的X形结构,用它替换了传统Sepic电路中的输入电感,二极管D1、D2使电流单向流动,防止对输入电源Ui反充电和电容C0通过电感L3放电,Q为开关管,导通比为D,通过调节D来实现电路的升降压功能,电容器C3作为输入到输出主要的能量转换元件。
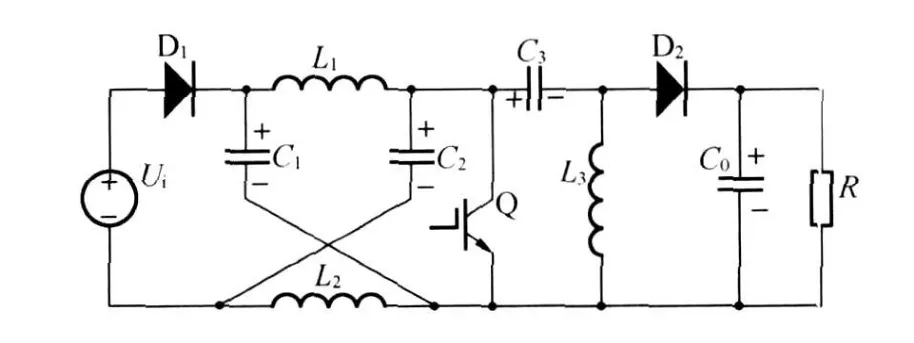
图1 Z源调压电路的原理图Fig.1 Z source voltage adjusting principle
由图1可见,假设C1和C2电容值相等且很大, L1和L2电感值相等且很大,故由C1、C2、L1和L2连接成的Z源网络结构是对称的,因此UC1=UC2, UL1=UL2,Z源网络相对传统电压源和电流源而言,具有既可开路又可短路的独特优点,因此为变换主电路的升压或降压提供了一种机制,藉此可将任何形式的电源耦合到任何形式的主变换器电路中,以向任何形式的负载供电[5-6],Z源调压电路是用Z源网络替换传统Sepic电路中的输入电感而构成的,此结构中在开关导通比D<0.5时就可以实现传统Sepic电路的升降压功能,从而弥补了传统Sepic电路实现升压时导通比D>0.5甚至更大的不足。
2 Z源调压电路工作原理分析
2.1 在分析稳态特性时的假设
1)开关管、二极管均为理想元件,可以瞬间导通截止而且导通时压降为零,截止时漏电流为零。
2)电感、电容为理想元件,电感工作在线性区域而未饱和,寄生电阻为零,电容的等效电阻为零。
3)输出电压中的纹波电压与输出电压的比值小到允许忽略。
4)电感电流为连续状态,即电路工作在连续工作模式下。
5)电容C1、C2、C3上的电压纹波与其平均值之比很小,这样电容电压在整个周期中可以认为是恒定的,设恒定值为[4]UC1=UC2=UC,UC3。
2.2 工作过程分析
根据开关管的工作状态,Z源调压电路有两个工作状态:
1)开关管工作在导通状态,即在TON期间,等效电路见图2,在 TON期间,由于Q的导通,电容C1、C2、C3处于放电状态,分别通过Q对L1和L2、L3储能,把内部储存的电场能量转化为磁场能量储存到电感中,电感电流的方向如图中所标注,电感L1、L2和L3处于储能状态,流过的电流 I1、I2和I3线性上升,其两端电压dt和为正值,方向如图2中所标注的,从而使二极管D1阴极电位升高,D1承受反向压降而截止,输入电源Ui被切除,二极管D2阳极电位降低,D2也承受反向压降而截止,此时电容C0处于放电状态,对负载R供电。
此状态下的电压关系为:
在C1、C2的放电回路中可得UL1on=UL2on=UC
2)开关管工作在关断状态,即在Tof f期间等效电路如图3所示,在期间,由于Q的截止,电感和处于释能状态,流过的电流和线性下降,其两端电压UL1off、UL2off和UL3off为了维持电感中的电流方向不变而改变方向,方向如图3中所标注,从而使二极管阴极电位降低,D1承受正向压降而导通,二极管D2阳极电位升高,D2也承受正向压降而导通,D1导通把输入电源Ui接入,和电感L1、L2、L3一起既给电容C1,C2,C3和C0充电,同时也向负载R供电。
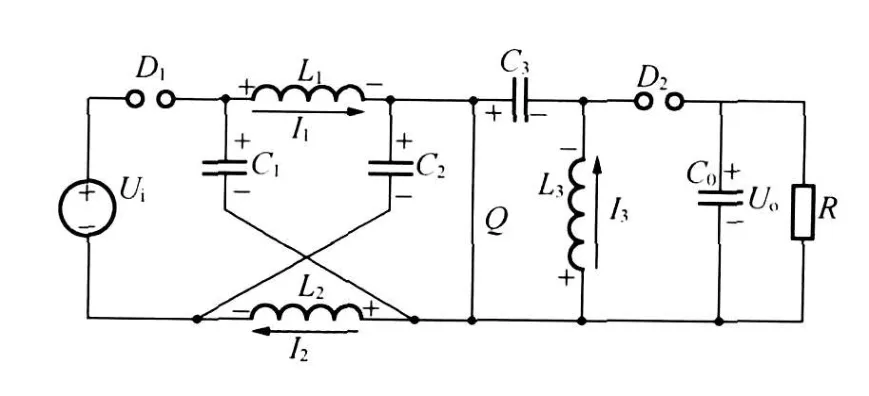
图2 开关管Q导通时等效电路Fig.2 Equivalent circuit when conduction pipe Q connected
此状态下电压关系为:
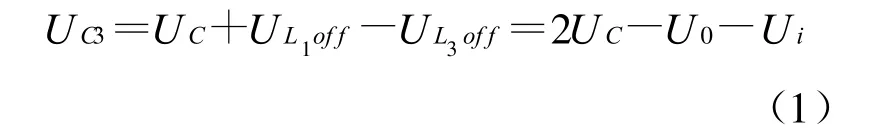

图3 开关管Q关断时等效电路Fig.3 Equivalent circuit when conduction pipe Q not connected
2.3 升压比的推导
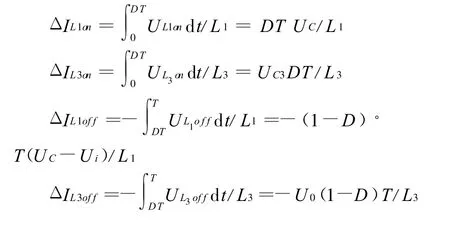
由于稳态时电感电流在开关导通和关断期间的变化量相等[4],即:
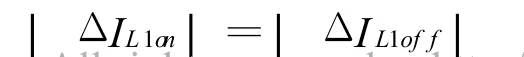
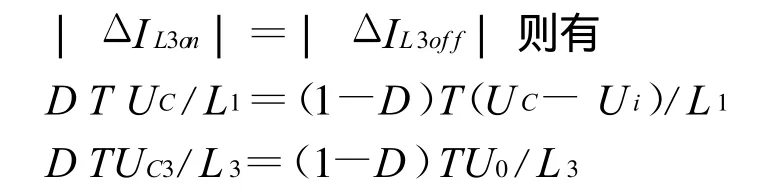
进一步整理得:
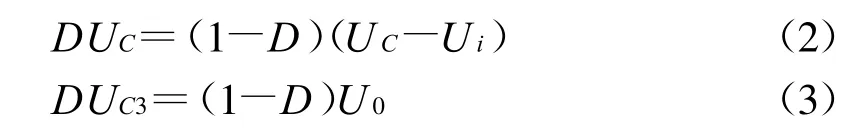
由式(1)-式(3)得:
升压比B=U0/Ui=D/(1-2D)其中0<D<0.5。
可见在理论上,Z源调压电路当导通比D<0.5时就能实现传统Sepic电路的升降压功能,0<D<1/3时实现降压功能,1/3<D<0.5实现升压功能,而且能得到任意值的输出电压,因此理论上电压调节范围很大。
3 Z源调压电路与传统Sepic电路的比较
传统Sepic电路的升压比B=D/(1-D),而Z源调压电路的升压比B=D/(1-2D),现用MATLAB得出升压比B与导通比D的关系曲线见图4。
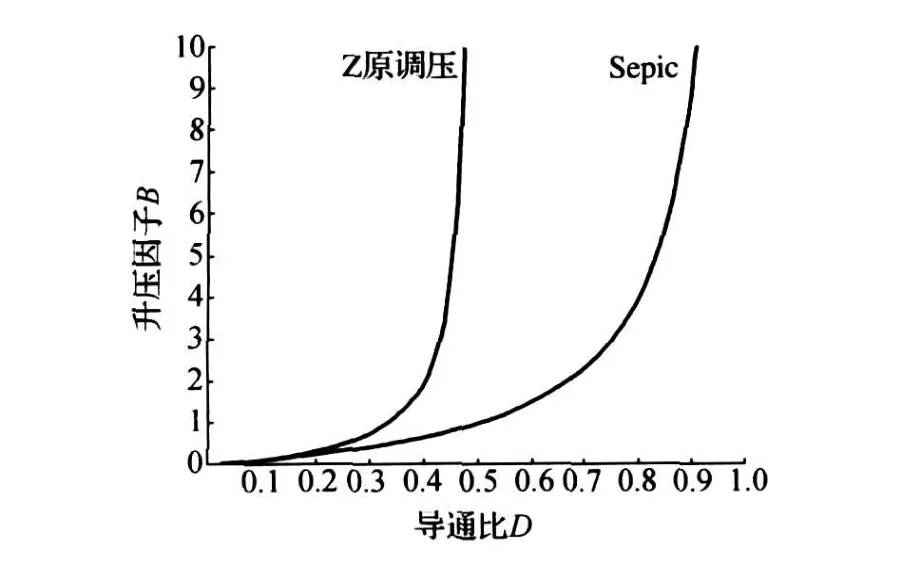
图4 升压比B与导通比D的关系曲线Fig.4 Relation between booster ratio and conduction ratio
由图4中曲线可见,对于Z源调压电路:当D<1/3时B<1即实现降压功能,当D>1/3时,B>1即实现升压功能,且当导通比D接近0.5时升压比可无穷大;而对于传统的Sepic电路而言,当D<0.5时B<1即实现降压功能,当D>0.5时,B>1即实现升压功能,且当导通比D接近1时升压比才可无穷大。由图中还可得出在相同的导通比下,Z源调压电路的升压比大于传统Sepic电路的升压比。
4 仿真结果
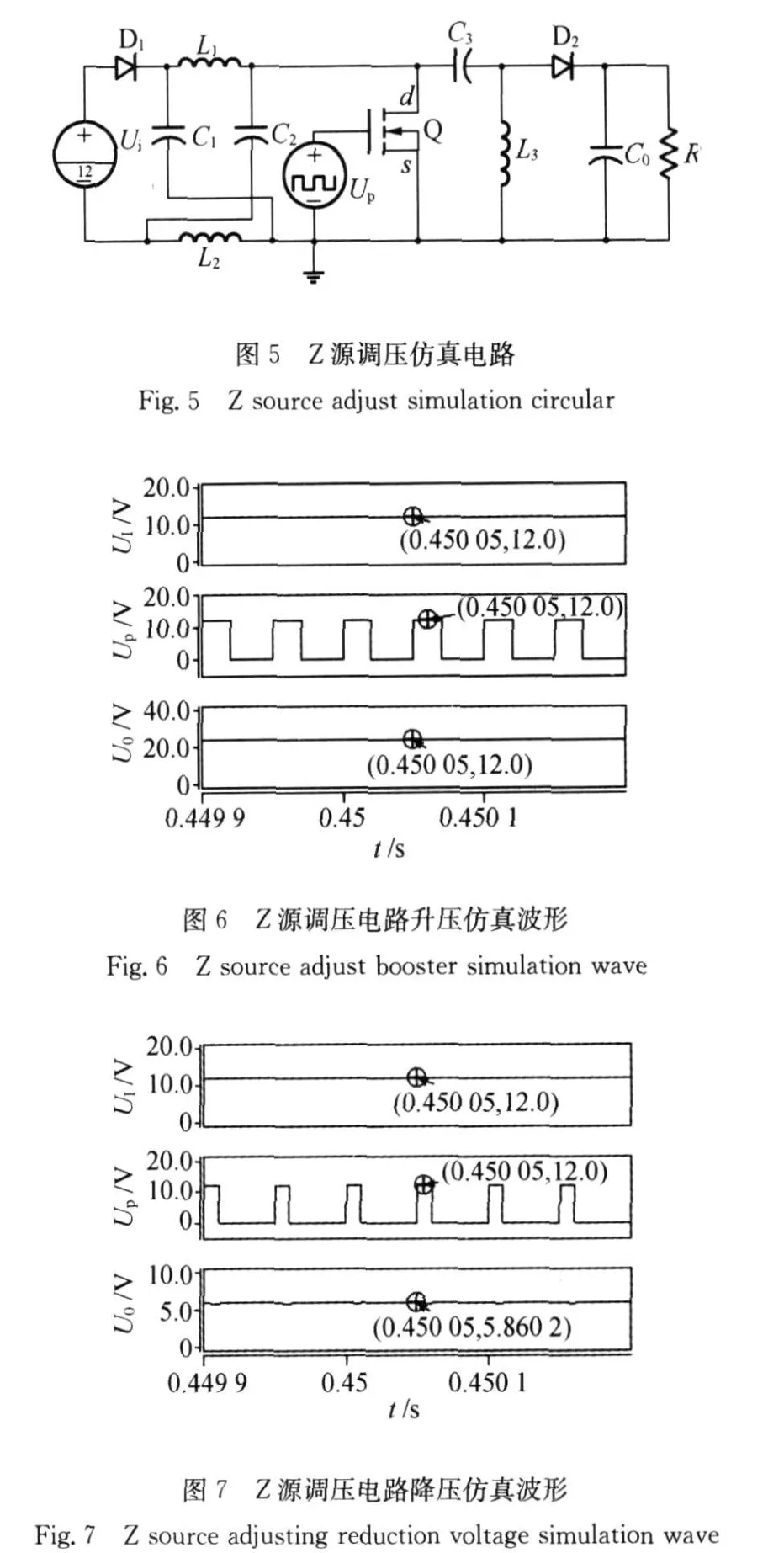
现对Z源调压电路的升压和降压分别进行仿真,仿真电路图见图5。
4.1 升压仿真
设输入电压Ui=12 V,导通比D=0.4,用SABER进行仿真得到结果见图6。图6中给出了脉冲电压Up、输入直流电压Ui和输出直流电压U0的时域波形,由理论计算得:D=0.4、Ui=12 V时,升压因子B=2,输出电压U0=24 V,由图6中查得U0=23.831 V,考虑到管压降等因素的影响,升压仿真结果与理论分析相符。
4.2 降压仿真
设输入电压Ui=12 V,导通比D=0.25,用SABER进行仿真得到的结果见图7。图7中给出了脉冲电压Up、输入电压Ui和输出电压U0的时域波形,由理论计算得:D=0.25、Ui=12 V时,升压因子B=0.5,输出电压U0=6 V,由图7中查得U0=5.860 2 V,考虑到管压降等因素的影响,降压仿真结果也与理论分析相符。
5 试验结果
用图1电路构建实验电路,采用仿真参数进行升降压实验,实验波形见图8,在图8的波形中,1路是输入电压Ui波形,2路是开关管的驱动电压Up波形,3路是输出电压U0波形。
在升压实验中,输入电压Ui=12 V,开关导通比D=0.4,升压因子B=2,由图8可见,输出电压U0=23.8 V;在降压实验中,Ui=12 V,开关导通比D=0.25,因子B=0.5;由图9可见,输出电压U0= 5.8 V,考虑到管压降和线路损耗的影响,试验结果与理论分析和仿真结果相符合。
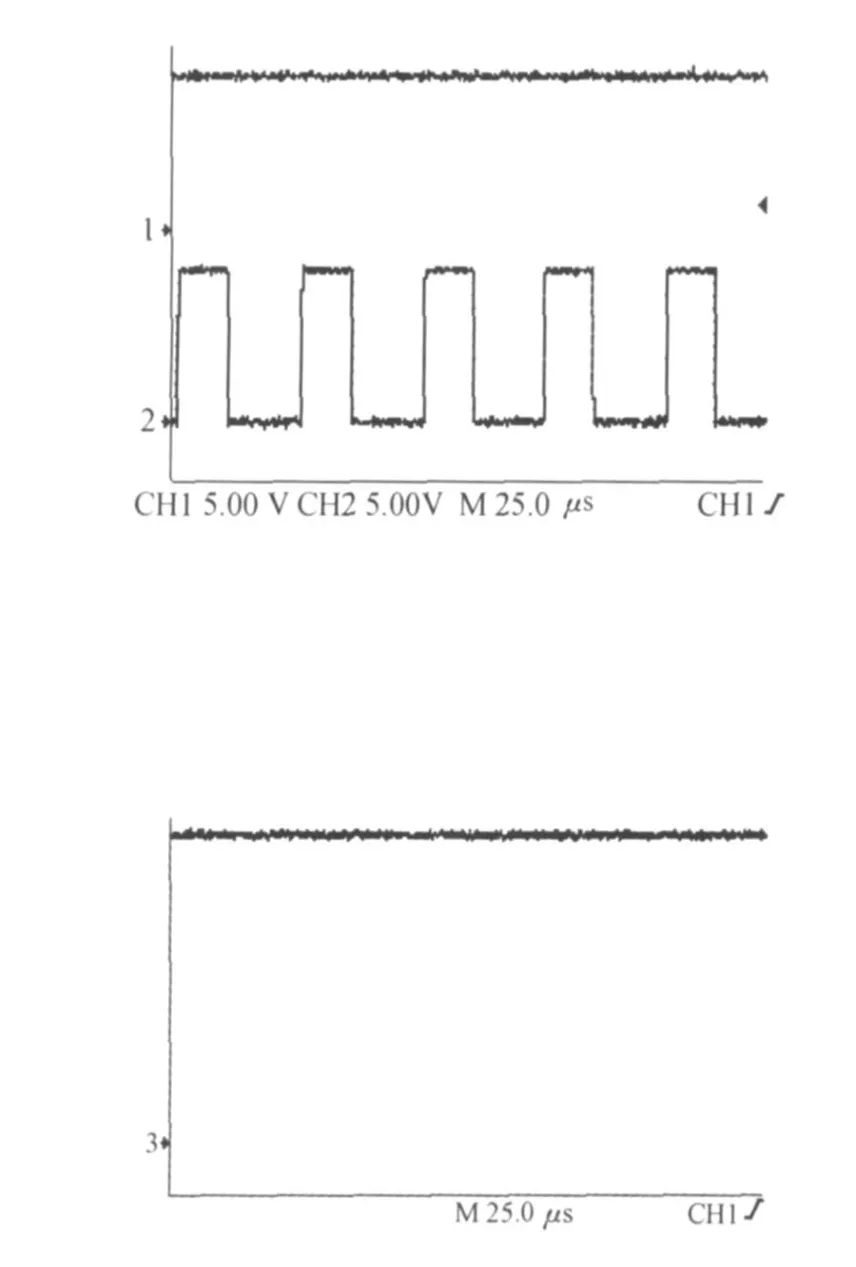
图8 Z源调压电路升压实验波形Fig.8 Z source adjusting booster voltage simulation wave
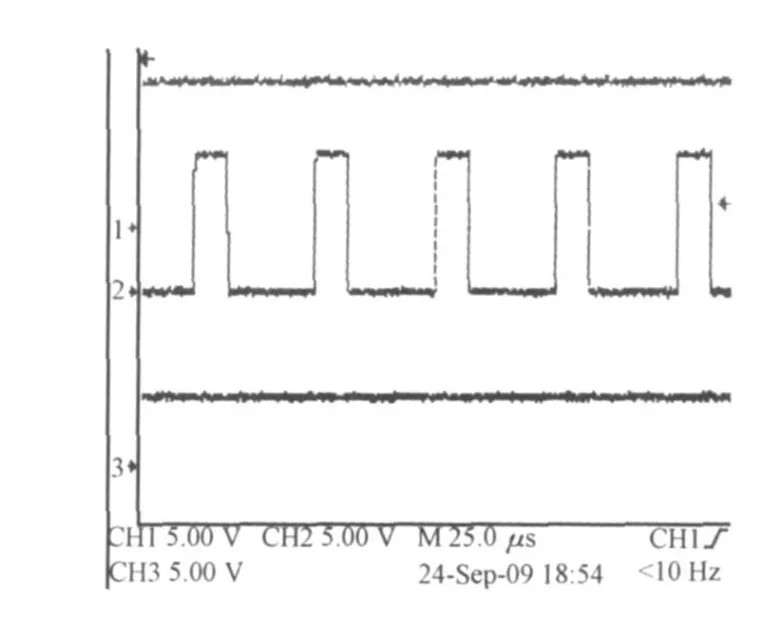
图9 Z源调压电路降压实验波形Fig.9 Z source adjusting reduction voltage test wave
6 结 语
本文提出了一种基于Z源的新型直流升降压拓扑,该拓扑将Z源网络和传统Sepic电路结合在一起,可以在开关导通比D<0.5的情况下进行升降压调节,克服了传统Sepic电路在升压比高时导通比D过大甚至接近1的缺陷。
[1] 王利民.Z源直流变换器[J].电气应用,2005,24(2):123.
[2] 彭方正.Z源升压变换器[J].电气传动,2006,36(1):28.
[3] 王利民.阻抗源直流变流器的研究[D].杭州:浙江大学,2006.
[4] 张占松.开关电源的原理与设计[M].北京:电子工业出版社, 1998.
[5] Peng F Z,Shen M S,Qian Z M.Maximum Boost Control of the Z—Source Inverter[J].IEEE Trans.on Power Electron.2005, 20(4):833-838.
[6] Fnag2Peng.Z-Soucre Inverter for Motor Drives[C]//In Proc.of IEEE PESC,2004 Conference,2004.Volume:1,3-7 Oct.2004:147.
