用量子化学参数预测聚合物玻璃化温度

颜炜伟

(湖南工程学院化学化工学院,湘潭 411104)

用量子化学参数预测聚合物玻璃化温度

颜炜伟

(湖南工程学院化学化工学院,湘潭 411104)

在B3LYP/6-31G(d,P)水平上对聚合物单体进行密度泛涵理论算,得到4个量子化学参数(分子偶极矩μ,平均极化率α,熵S及内能Eint)用来建立聚合物玻璃化转变温度Tg的人工神经网络(ANN)模型.误差反向传播的人工神经网络方法用来拟合4个参数与 Tg可能存在的非线性关系.通过试差法调整网络参数得到最佳网络条件.模拟最佳网络模型4-4-1,结果表明模拟值与实验值非常接近,训练集与测试集的均方根误差(rmse)分别为17.878K和22.685K,该结果优于线性回归法得到的结果.

量子化学参数;聚合物;玻璃化转变温度;人工神经网络

0 引 言

聚合物材料玻璃化转变温度Tg是指高聚物无定形部分从冻结状态到解冻状态的一种松弛现象,而不像相转变那样有相变热,它是一种二级相变(高分子动态力学中称主转变).在 Tg以上,聚合物处于高弹态,继续升温,整个分子链开始运动而表现出粘流性质,弹性大,如室温下的橡胶.在Tg以下,聚合物处于玻璃态,分子链和链段都不能运动,只是构成分子的原子(或基团)在其平衡位置作振动,材料脆性较大,如室温下的塑料.Tg是非晶态高分子材料固有的性质,是高分子运动形式转变的宏观体现,它直接影响到材料的使用性能和工艺性能,因此长期以来它都是高分子物理研究的主要内容.由于高分子结构的复杂性,其分子运动也就更为复杂和多样化.Tg既是非晶态聚合物的一个重要的物理性质,也是凝聚态物理基础理论中的一个重要问题和难题,涉及动力学和热力学的众多前沿问题.玻璃转变的理论虽然一直在不断的发展和更新.但对玻璃转变现象作出完整的理论解释仍是一个极具挑战性的课题.

由于聚合物的玻璃化转变在一个相对较大的温度范围内发生,并且除了分子结构对Tg有影响之外,其它如测量方法,测量条件等因数都对 Tg产生影响,不同的文献报道的Tg值会有所差异[1,2].结构与性能定量关系(QSPR)研究是采用数学统计方法寻找和建立物质结构参数与性能之间的定量关系[3,4].一旦这种关系被建立则可以用来预报其他未知物质的性质,然后可以有选择的合成制备期望物质.从而节省大量的人力、物力,加快新物质的开发.因此用结构-性能定量关系(QSPR)方法预测聚合物材料Tg具有重要意义.

在Tg的QSPR研究中,比较常用的有基团贡献法[1].该法虽然简便易用,但属于经验方法,没有考虑邻近基团的影响,并且只限于已有的基团,推广受到限制.Bicerano[2]采用溶度参数及13个结构参数关联Tg得到模型相关系数R为0.9749,标准误差s为24.65 K.但该模型并没有受到检验.近年来有学者采用人工神经网络(ANN)建立Tg的QSPR模型.Mattioni与Jurs[5]建立的两个模型分别含有10个和11个参数,两个模型测试集给出的均方根(rmse)误差均大于21 K.Liu与Cao[6]的ANN模型隐含层为两层.网络参数或隐含层过多容易产生过拟现象,不利于模型的推广.本文对聚合物的单体开展精确计算,采用ANN方法得到只含4个参数、隐含层取一层的聚合物 Tg的QSPR模型.

1 方 法

本文收集了86种聚合物的Tg实验数据[7].这些聚合物包括19聚苯乙烯和67聚丙烯酸酯,单体结构均为H2C=CR1R2.它们 Tg数值范围较宽:198～464 K.将这些聚合物分为训练集和测试集.由训练集建立模型,再由测试集对模型进行检验.

由于聚合物分子量很大,且分布广,要对整个聚合物分子进行精确计算存在困难.但聚合物是由单体形成,因此聚合物的性质必然与单体结构有关.密度泛函理论认为,分子的总能量及性质取决于体系电荷密度的分布.通过对电子动能和势能的平均化处理,借助变分法或数值方法,可以得到Schrädinger方程的近似解.在密度泛函理论中,体系状态的基本表征是电子密度而不是波函数.由密度泛函方程同样可以得到相当准确的体系能量以及其他性质.对大体系,DFT耗时比传统的从头算要少1～2个数量级.密度泛函理论(DFT)考虑了电子的相关能,并且所需计算机空间和机时相对较少,因而成为当前广泛使用的方法.

在量子化学计算中,根据体系的不同,需要选择不同的基组,构成基组的函数越多,基组便越大,对计算的限制就越小,计算的精度也越高,同时计算量也会随基组的增大而剧增.极化基组如6-31G(d,p)或6-31G(d)已得到广泛应用[8-11].因此本文采用DFT(B3LYP)方法在6-31G(d,p)基组水平上对聚合物单体进行模型优化和计算.根据经典的化学理论,所有的化学作用在本质上均与分子的静电(极性)或轨道(共价)有关.而分子中原子最负电荷q-、氢原子最正电荷q+、偶极矩μ以及平均极化率α是4个重要电性参数.热化学参数熵S、内能Eint及分子的总能量ET与分子的构象及体系大小有关.在本文中共计算了此7个量子化学参数.

人工神经网络(ANN)具有非线性变换、并行处理、自适应、自学习能力、自组织特性、容错性及外推性等特性.近年来ANN在计量化学中得到了越来越多的应用.它无需人们预先确定系统的模型,可根据系统输入(如分子结构参数)和输出(各种物理或化学性质)找到它们之间的非线性关系,从而获得一个反映分子结构与物质性质内在规律的数学模型,因此,运用ANN能用于物质的QSPR研究.

通常反向传播算法的神经网络BPANN由输入层、隐含层、输出层构成.BP算法的学习过程由正向传播和反向传播组成.在正向传播过程中,如果输出层不能得到期望的输出,则转入反向传播,将误差信号沿原来的连接通路返回,修改各节点间的权重值,反复运行直至误差信号最小或达到最大学习次数时为止.在实际运算中用一组样本构成训练集,令其学习,按一定的学习规则调整连接权重值,将学习得到的知识总结成规律并保存,再用这保存的组权重分布,根据预测集样本的输入参数算出预测集样本结果.

适当的网络参数有助于ANN的学习.采用逐步线性回归方法选择的参数作为输入层,隐含层取一层,隐含层节点数根据试差法确定,以训练集和测试集均方根误差(rmse)之和最小为判断依据.以目标性质Tg作为输出层.

2 结果与讨论

通过对训练集66个样本与7个量子化学参数进行逐步线性回归分析,结果有4个参数进入相对最佳线性模型.4个参数的特征见表1.最佳线性模型及相应的统计参数如下:

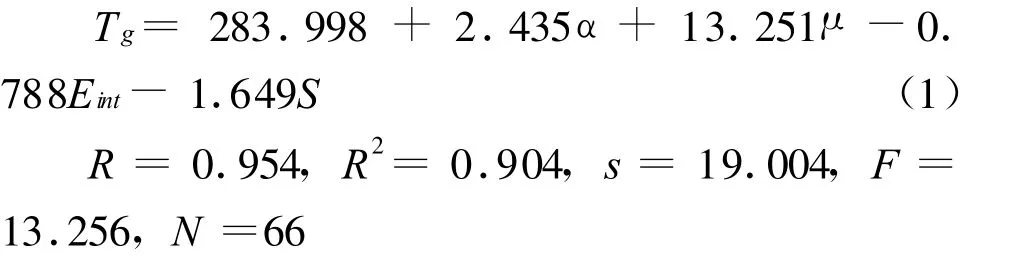
式中R为相关系数,s为标准误差,F为Fischer比值,N为样本数.

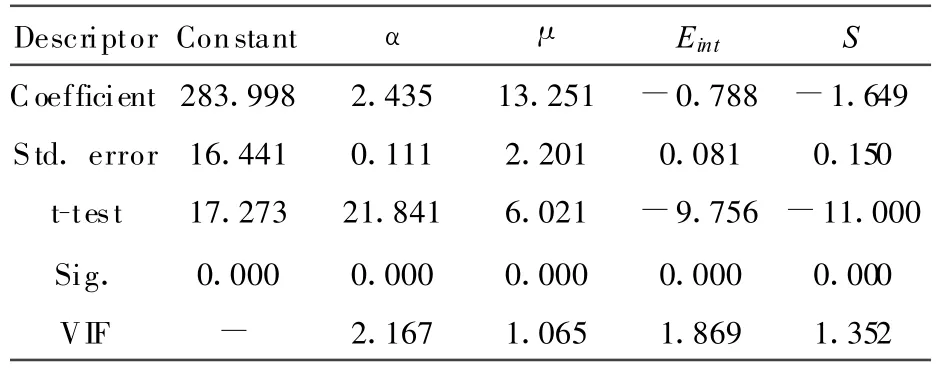
表1 模型所用的4个参数特征

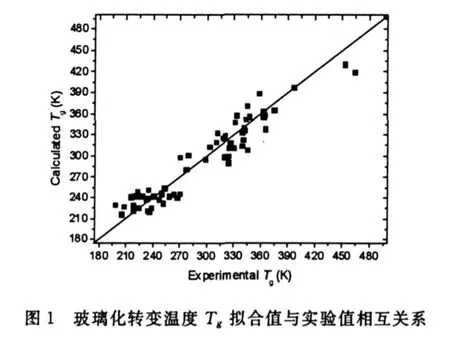
然后以此4个参数作为特征向量构成输入层.根据调整参数得到最佳的网络模型结构为4-4-1,其允许误差为0.00001,动态参数为0.6,参数SIGMOID为0.9,最大训练次数为5000.训练集与测试集的rmse分别为17.878 K和22.685 K.人工神经网络的拟合值和预测值与实验值的关系分别见图1和图2.本文结果小于或接近文献所报道的rmse误差[2,5,9,10];而网络结构比其他模型更简单.本文线性模型的训练集与测试集的 rmse分别为18.259 K和24.714 K,该结果均大于ANN相应的rmse值.表明4个参数与Tg存在明显的非线性关系,用ANN建立Tg模型更为合理.

表1中Sig.值小于默认值0.05,因此所有的参数均为显著性参数.并且有VIF＜3,远小于默认值10,表明这些参数之间不存在严重的多重共线性问题.即这些参数能从不同的侧面反映目标性质Tg.

Tg是指聚合物链段从冻结到运动(或反之)的一个转变温度,而链段运动是通过主轴的单键内旋转来实现的,因此,凡是能影响聚合物链柔性和分子间作用力的的因素,都对Tg有影响.减弱聚合物链柔性或增加分子间作用力的因数,如极性基团使Tg增加.而聚合物分子之间的作用力包括范德华力(静电力、诱导力和色散力)和氢键.静电力是极性分子之间的引力.极性分子都有永久偶极,永久偶极之间的静电相互作用的大小与分子偶极的大小和定向程度有关.诱导力是极性分子的永久偶极与它在其他分子上引起的诱导偶极之间的相互作用力.诱导力不仅存在极性分子与非极性分子之间,也存在于极性分子与极性分子之间.它的大小与分子的极性和变形性等有关.色散力是由于非极性分子之间,由于组成分子的正、负微粒不断运动,产生瞬间正、负电荷重心不重合,而出现瞬时偶极而引起的.分子量越大,色散力越大.当然在极性分子与非极性分子之间或极性分子之间也存在着色散力.分子极性大小用偶极矩 μ来度量,它的极化率是原子极化、电子极化与定向极化的总和.对于非极性分子,若极化率α越大,则在外电场诱导出的偶极矩越大.因此分子的量子化学参数偶极矩μ和平均极化率α可描述聚合物分子之间的范德华力的相对大小:参数μ和α越大,聚合物分子之间的作用力也越大.因此μ和α与Tg正相关.

根据聚合物玻璃化转变的自由体积理论,聚合物的体积是由两部分组成:聚合物链本身所占的体积和聚合物链间未被占据的空隙,即自由体积.自由体积是分子链进行构象转变和链段运动所需的活动空间.当聚合物自由体积比例较大时,分子链进行构象转变和链段运动比较容易,相应的Tg也低.而分子的量子化学参数熵S和内能Eint能反映分子体系的大小及自由体积的相对值.参数S和Eint越大,表明聚合物分子自由体积的相对值越大,链的构象转变和链段运动相对更容易,Tg值更低.因此S和Eint与Tg负相关.

3 结 论

本文用人工神经网络方法得到的QSPR模型精度、稳定.ANN的训练集与测试集的rmse分别为17.878 K和22.685 K.其结果小于或接近文献所报道的rmse误差,但本文所得模型更简单,且优于线性回归法得到的结果.研究表明4个量子化学参数(μ、α,S及Eint)与 Tg存在明显的非线性关系,用ANN建立Tg模型是合理的.

[1]van Krevelen DW.Properties of Polymers,Their Estimation and Correlation with Chemical Structure[M].2nd ed.Elsevier,Amsterdam,1976.

[2]Bicerano J.Prediction of Polymer Properties[M].2nd ed.New York:M arcel Dekker Inc,1996.

[3]禹新良,王学业,高进伟,等.用量子化学参数研究烯烃聚合物定量构效关系[J].化学学报,2006,64(7):629-636.

[4]禹新良,张仕华,王学业.用量子化学参数预测烯烃聚合物介电常数[J].湖南工程学院学报,2008,18(4):65-68.

[5]Mattioni BE,Jurs PC.Prediction of Glass Transition Temperatures from M onomer and Repeat Unit Structure using Computational Neural Networks[J].Journal of Chemical Information and Computer Sciences,2002,42:232-240.

[6]Liu Wangqiang Cao Chenzhong.Artificial Neural Network Prediction of Glass Transition Temperature of polymers[J].Colloid&Polymer Science,2009,287(7):811-818.

[7]Brandrup J,Immergut EH,Grulke EA.Polymer Handbook[M].4th ed.Wiley,New York,1999.

[8]Yu Xinliang,Yi Bing,Wang Xueye.Prediction of Refractive Index of Vinyl Polymers by Using Density Functional Theory[J].Journal of Computational Chemistry,2007,28:2336-2341.

[9]Yu Xinliang,Yi Bing,Wang Xueye.Predicton of the Glass Transition Temperatures for Polymers with Artificial Neural Network[J].Journal of Theoretical and Computational Chemistry,2008,7(5):953-963.

[10]Yu Xinliang,Yi Bing,Wang Xueye,et al.Correlation Between the Glass Transition Temperatures and Multipole Moments for Polymers[J].Chemical Physics,2007,332:115-118.

[11]Yu Xinliang,Yu Wenhao,Yi Bing,et al.Artificial Neural Network Prediction of Steric Hindrance Parameter of Polymers.Chemical Papers,2009,63(4):432-437.

Prediction of Glass Transition Temperatures of Polymers by Using Quantum Chemical Descriptors

YAN Wei-wei
(School of Chemistry and Chemical Engineering,Hunan Institute of Engineering,Xiangtan 411104,China)

Density functional theory(DFT)calculations are carried out at the B3LYP/6-31G(d,p)level,and four quantum chemical descriptors calculated from monomers of polymers(the dipole moment i,the average polarizability of the molecule α,the entropy S,and the thermal energy Eint)are used to develop an artificial neural network(ANN)model for glass transition temperature(Tg).The typical back-propagation(BP)ANN is employed for fitting the possible non-linear relationship between the four descriptors and Tg.The optimal condition of the neural network is obtained by adjusting various parameters by of the trial-and-error method.Simulated with the final optimum BP neural network 4-4-1,the results show that the fitted Tgvalues are in good agreement with the experimental data,with the root mean square errors(rmses)for the training set and the test set being 17.878K and 22.685K,respectively,which are superior to those obtained by multiple linear regression analysis.

quantum chemical descriptors;glass transition temperature;polymer;artificial neural network

O6-04;O631

A

1671-119X(2010)02-0056-04

2009-12-08

湖南省教育厅科研资助项目(07C205)

颜炜伟(1977-),男,硕士,研究方向:化学工程及模拟.