基于信息熵的导流方案模糊模式识别方法

汪 莲,琚泽进

(合肥工业大学土木与水利工程学院,合肥 230009)

基于信息熵的导流方案模糊模式识别方法

汪 莲,琚泽进

(合肥工业大学土木与水利工程学院,合肥 230009)

针对导流方案综合评价中各指标的不相容性,利用模糊模式识别的方法,将导流方案的多个指标合成为一个与最优评价集的相对贴近度,用来描述导流方案的综合效益.以可供选择的4种导流方案为例进行了评价,得到综合效益最优方案.

导流方案;模式识别;模糊识别;加权Hamming贴近度

0 引 言

施工导流工程是在水利枢纽工程建设过程中对河床水流进行控制的全面部署,是水利枢纽工程施工中的关键性施工措施.导流方案优选对导流工程的规模、工期及其可靠性影响极大,而且在大型水利枢纽工程建设过程中的导流工程的好坏 ,还涉及发电、灌溉、航运、供水等其他国民经济部门的利益,所以在水利工程建设中,要缩短建设工期,降低工程投资,必须做好施工导流的方案比选工作.在施工导流工程中,通过对影响导流标准的工程投资、建设工期、风险损失以及导流风险各个要素进行定量多目标分析,从总体上优化导流标准.不少学者在这方面进行过探讨,建立了一些决策模型.如:苏勤、周建旭[1]的多目标系统模糊决策法,周宏安,李炳杰[2]及尚梅,金维兴[3]的多属性模糊决策法,张清河,赵克勤[4]的模糊层次评价法,牛午生[5]的多层次多目标决策法,仇一颗[6]的风险度法,杨兆兰[7]的多方案多指标线性加权模型,周宜红、肖焕雄[8]的灵敏度分析,徐森泉、胡志根[9]的基于熵权的多目标决策法,Yager R R、Detynecki M[10]等的可能度法等.

本文针对导流方案综合评价中各指标的不相容性,利用模糊模式识别的方法,将评价导流方案的多个指标合成为一个与最优评价集的相对贴近度,用来描述导流方案的综合效益.以可供选择的4种导流方案为例进行了评价,得到综合效益最优的方案.

1 各指标权重系数的计算

由于原始数据的含义及量纲不同,不利于比较,因此在建立评价模型前需要利用公式(1)进行数据标准化处理,消除量纲,使处理后的数据取值区间限制在0～1内.

式中,rik(i=1,2,…,m)称为被评价方案指标值 fik与标准方案A0中各对应指标 fok的同一度.

评价模型中权重系数确定影响与控制着评价结果的准确性.在信息论中,熵值反映了信息的无序化程度,可以用来度量信息量的大小,某项指标携带的信息越多,表示该项指标对决策的作用越大,此时熵值越小,即系统的无序度越小.因此可用信息熵评价所获信息的有序度及其效用,即由评价指标值构成的判断矩阵来确定各评价指标的权重.其主要计算步骤如下[11].

式中:fmax,fmin分别为同一评价指标下最满意者和最不满意者的值.(越大越满意或越小越满意).可见,当hik=0时,lnhik无意义,则需对hik按以下公式加以修正,

2 基于加权Hamming贴近度的改进模糊模式识别模型

模糊模式识别是模糊集合论应用的重要方面之一,它的主要任务是让机器能模拟人的思维方面,对带有模糊性的客观事物进行识别和归类.在现实生活中,对于要识别的对象不是单个确定的元素,而是论域上的子集或模糊集,在识别中采用模式识别的间接方法.在识别中采用择近原则[12].

设 Ai∈F(U)(i=1,2…,m),对给定 A0∈F(U),若 ∃j∈{1,2,…,m},使得:

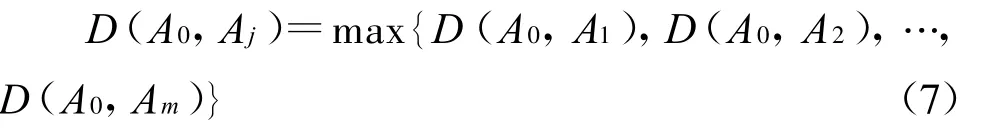
则认为Aj与A0最接近,而应把 Aj归于模式A0.

式中Ai(i=1,2,…m)为各待评方案的标准化后的指标值矩阵,A0为理想方案标准化后的指标值矩阵.而对于贴近度D(A0,Ai)的计算,利用Hamming贴近度公式,传统的Hamming贴近度公式为:

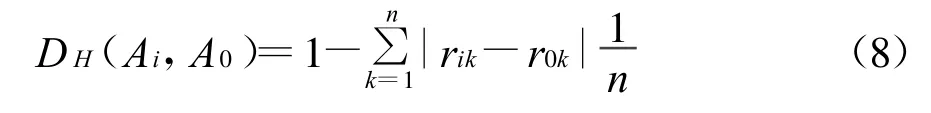
未反映指标值及权重确定时所具有的不确定性.在这里对此进行改进,考虑个指标权重的影响得到加权Hamming贴近度公式:

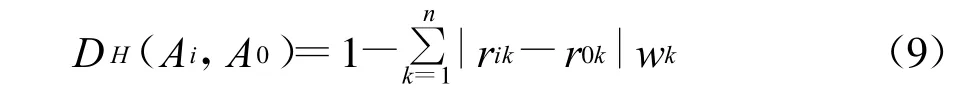
其中,wk(k=1,2,…,n)是加于 rik上的权重=1.rik为Ai方案中对应的第k个指标标准值(k=1,2,…,n),r0k为A0方案中对应的第k个指标标准值(k=1,2,…,n).

3 在导流方案评价中的应用

本文采用文献[1]的数据,评价中共选用3项导流方案要素评价指标,指标实测值详见文献[1],指标归一化后数值见表1所示.理想方案:

其中:导流投资、施工强度、经济损失均为越小越优型指标

利用公式(1)对导流方案的各量化指标进行标准化处理,使处理后的数据取值区间限制在0～1内,标准化后的数据见表1.在这里的四种方案依次为A1,A2,A3,A4.且

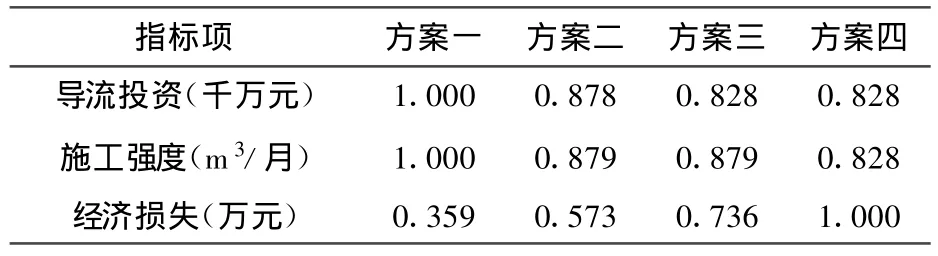
表1 标准化后的数据值

理想方案标准化后的数据值为:

对3个方案按照式(2)-(6)计算出各评价因子的熵权,即为:0.092,0.080,0.828.

根据式(9)计算加权Hamming贴近度:

由此可知,4种导流方案的优劣排序为:方案四＞方案三＞方案二＞方案一.即可认为方案四为最优理想方案,这与文献[1]一致.

4 结 论

导流方案综合评价是一个较为复杂的问题.应用模糊模式识别对导流方案进行综合比选,计算待评价方案与最优方案的加权海明贴近度,进而求得最优方案,数学表达简明,物理意义明确,而且评判结果合理可取,方法切实可行.且本文在确定各项评价指标的权重时引入信息论中的熵值理论,通过信息熵反映实测数据本身的效用值确定权重,使得权重分配有了一定的理论依据.

[1]苏 琴,周建旭.多目标系统模糊决策法在导流标准比选中的应用[J].中国农村水利水电,2007,12:82-84.

[2]周宏安,李炳杰.基于相对隶属度的模糊信息的多目标决策法[J].陕西工学院院报,2004,20(4):77-80.

[3]尚梅,金维兴.基于多目标模糊决策理论的工程项目设计方案决策[J].经济师,2004,(6):269-274.

[4]张清河,赵克勤.多指标施工方案优选的新方法[J].建筑管理现代化,2005,(3):42-44.

[5]牛午生.浅议百色枢纽施工导流标准的选择[J].云南水力发电,1999,15(3):75-76.

[6]仇一颗.模糊层次评价在逆作法施工方案优选中的应用[J].湖南农业大学学报(自然科学版),2005,31(1):91-94.

[7]杨兆兰.多目标决策模糊物元分析[J].甘肃联合大学学报(自然科学版),2005,19(3):12-14.

[8]周宜红,肖焕雄.过水围堰导流标准的多目标风险决策[J].人民长江,1994,25(3):20-24.

[9]徐森泉,胡志根,刘全,等.基于熵权的导流标准多目标决策分析[J].中国农村水利水电,2004,(8):45-47.

[10]Yager R R,Detynecki M,Bouchon2Meunier B.A Context-De-pendent Method forOrdering Fuzzy Numbers Using Probabilities[J].Information Sciences,2001,138:237-255.

[11]闫文周,顾连胜.熵权决策法在工程评标中的应用[J].西安建筑科技大学学报,2004,36(1):98-100.

[12]汪培庄,韩立岩.应用模糊数学[M].北京:北京经济学院出版社,1989.

Entropy-based Fuzzy Pattern Recognition Method of Diversion Programs

WANG Lian,JU Ze-jin

(School of Civil Engineering,Hefei University of Technology,Hefei 230009,China)

T his paper introduces the diversion program for the comprehensive evaluation of the incompatibility of various indicators,the use of fuzzy pattern recognition method,and a number of indicators of diversion programs combined into one set with the optimal evaluation of the relative proximity.The diversion program comprehensive benefits are described.With choice of four kinds of diversion programs as an example of the evaluation of comprehensive benefits,the best solution is obtained.

diversion program;pattern recognition;fuzzy recognition;hamming weighted proximity

TU3

A

1671-119X(2010)02-0079-03

2009-11-14

汪 莲(1959-),男,副教授,硕士生导师,研究方向:水工结构.

book=173,ebook=173