QTZ630塔式起重机臂架有限元分析
2010-03-17李常胜郭秀云梁建明张兰娣王少雷
李常胜 郭秀云 梁建明 张兰娣 王少雷
河北建筑工程学院
0 前 言
塔式起重机是现代工业与民用建筑的主要施工机械之一.QTZ630塔式起重机是为满足中高层建筑施工、设备安装而设计的新型起重运输机械,它广泛地适用于多层和高层民用建筑,多层大跨度工业厂房,及采用滑模施工的高大烟囱和筒仓等塔型建筑物的施工,也可用于港口,货场的装卸.本机性能先进,结构合理,操作简单,使用安全.主要特点起升高,附着时可达140米,工作幅度大,可达55米.
本设计按照整机主要性能参数,确定了吊臂的结构参数,并按照吊臂端部加载、跨中加载和根部加载三种工况分析.通过对吊臂作适当的简化,应用ANSYS软件建立吊臂有限元模型,对各工况施加载荷,进而得到各节点受力情况,及各单元所受轴向力、轴向应力大小,及各工况下吊臂的变形挠度大小,清楚地展现了各工况下吊臂的受力性能.从而获得吊臂的最终参数结果.
1 吊点位置的选择(见参考文献(4))
单吊点小车变幅臂架是静定结构,而双吊点小车变幅臂架是超静定结构.对于大幅度塔式起重机,采用单吊点同采用双吊点相比,在相同工况下,单吊点吊臂变形挠度大,臂架自重将会有明显的加大,致使用钢量加大,成本加大,采用双吊点,将会改善吊臂的受力状况,同单吊点相比,自重减轻5%-10%
由第一吊点位置L1=0.27 L,第二吊点为L2=L,初选第一吊点位置距吊臂根部为12.685 m,第二吊点取三个位置分别距吊臂根部距离为35.795 m,37.445 m,39.095 m.通过后续过程的有限元分析计算,分别对该三种组合进行分析,对比分析结果,选择最优组合.
2 有限元模型建立过程的几点简化
2.1 自重及风载荷的简化
对于吊臂自重,简化为集中力均加于上弦杆的节点上.风载荷作为集中力均加于迎风面下弦杆的节点处.
2.2 吊点处约束的确定
为与现实更为符合,此次建模将于实际情况一样将用拉杆限制吊点约束,再将拉杆的另一端,即塔顶处,加除一转动自由度以外的五个自由度给以约束,这样便能使分析结果更加与实际接近.
2.3 单元类型选择
通过对吊臂的简化,忽略吊臂间的联系,把吊臂看成均匀的空间钢架.上下弦杆设置为压弯单元,腹杆设置为空间链单元.
2.4 模型生成及分析过程
先生成节点,通过节点生成单元,再施加载荷,在施加载荷时,在每组吊点组合中,分别按三种工况加载,分别在吊臂最大有效幅度处,跨中处,吊臂最小有效幅度处.在分析中修改模型三次(三个吊点位置),每个模型分别按三个工况加载.
3 吊臂结构的有限元计算
3.1 分析流程及程序
此设计中吊臂结构的有限元分析计算采用了ANSYS软件,其整个分析程序流程图如图1:
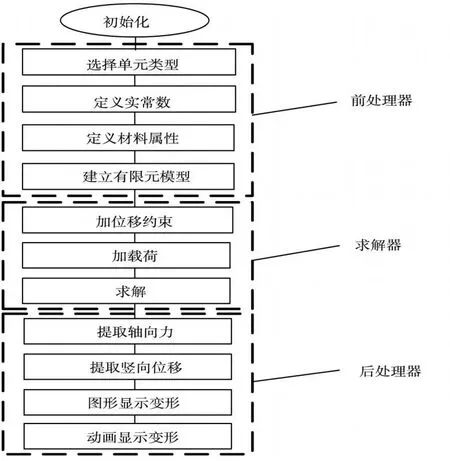
图1 吊臂结构有限元流程图
3.2 55米臂模型的建立
通过坐标生成节点,通过节点生成单元,忽略节间连接,把吊臂看成均匀的空间钢架,上下弦杆采用Beam4单元类型,腹杆采用Link8单元类型,第一吊点位置去距吊臂根部距离12.685 m,第二吊点位置分别取37.445 m与39.095 m两处一座比较.吊臂自重均加于上弦杆,工作载荷按在吊臂端部、跨中、根部三位置加载.如图2.
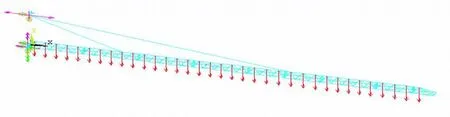
图2 加完自重及位移约束模型图
3.3 第二吊点位于37.445 m处的计算
对模型施加载荷和位移约束,即可对模型进行有限元计算,结果如图3、图4、图5.
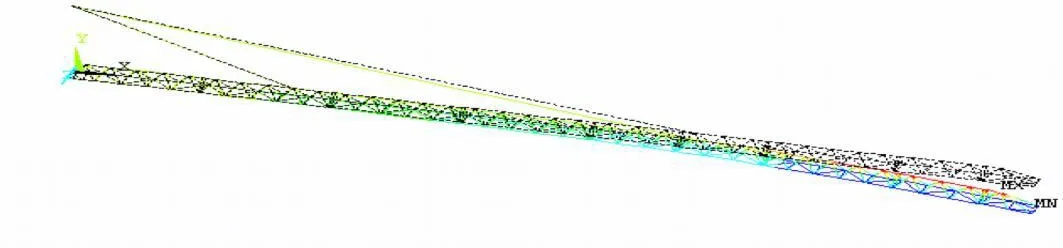
图3 工作载荷位于端部变形图
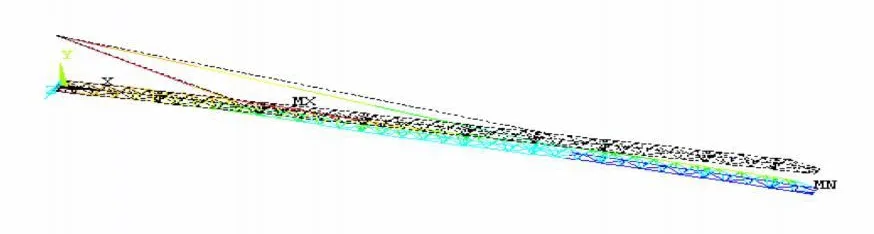
图4 工作载荷位于跨中变形图

图5 工作载荷位于吊臂根部变形图
3.4 第二吊点位于39.095处的计算
对模型求解的结果如图6、图7、图8.

图6 工作载荷位于端部变形图

图7 工作载荷位于跨中变形图
图8 工作载荷位于吊臂根部变形图
3.5 两种吊点位置计算结果的比较
对上述两位置的吊臂通过ANSYS有限元软件计算得出吊臂在不同工况下的最大挠度、单元轴向力最大值如表2.
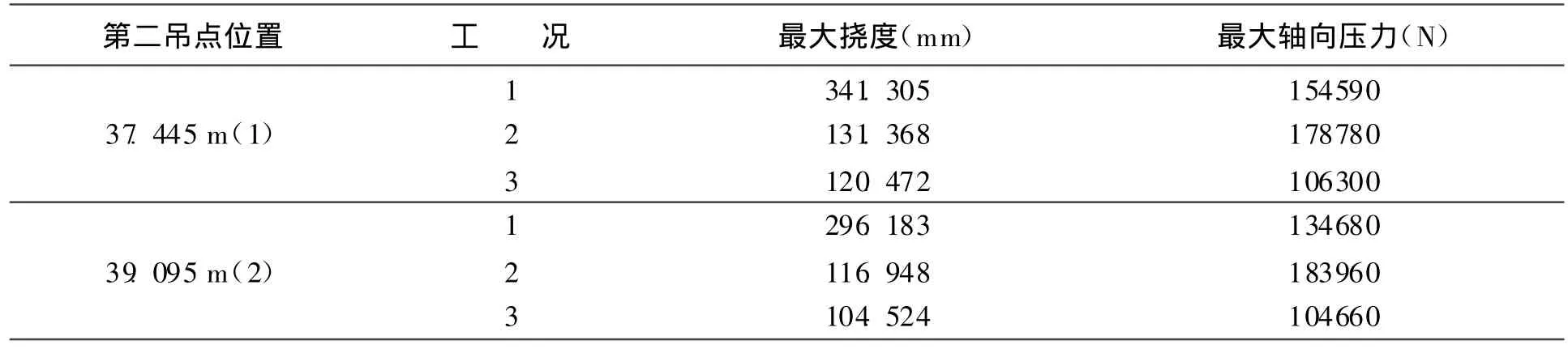
表2 两种计算结果比较
4 结 论
(1)吊臂为空间桁架结构,理论计算较为复杂,而应用ANSYS有限元软件计算则行之有效.
(2)通过ANSYS计算表明:吊点位置的不同对挠度及轴向压力有很大影响,综合分析第二吊点位于39.095 m处吊臂受力性能优于第二吊点位于37.445 m处.
[1]白葳、喻海良编著,通用有限元分析ANSYS8.0基础教程.北京:清华大学出版社,2005
[2]龚曙光主编,ANSYS基础应用及范例解析,北京,机械工业出版社,2003
[3]GB/T13792-92,塔式起重机设计规范,北京,中国标准出版社,1993
[4]刘佩衡主编.塔式起重机使用手册.北京:机械工业出版社,2002
