空间 6R串联机器人机构位置逆解新算法

黄昔光

(北方工业大学 机电工程学院,北京 100041)

廖启征

(北京邮电大学 自动化学院,北京 100876)

空间 6R串联机器人机构位置逆解新算法

黄昔光

(北方工业大学 机电工程学院,北京 100041)

廖启征

(北京邮电大学 自动化学院,北京 100876)

将倍四元数的复指数形式应用于串联机构位置逆解分析中,提出了空间 6R(R代表转动副)串联机构位置逆解新算法.基于倍四元数建立了空间 6R串联机构位置逆解的数学模型;然后,使用线性消元和 Dixon结式消元法,得到了 6×6的结式;由于采用未知转角的复指数形式,不需要提取任何公因式,可直接获得该机构位置逆解的一元 16次输入输出方程和全部 16组封闭解.最后通过数字实例证明了该方法无增根无漏根.算例表明算法简洁,易于程序实现,为串联机构位置逆解分析提供了新的理论基础.

串联机构;倍四元数;位置逆解

由转动副、移动副以及圆柱副组成的空间串联机构,结构类型有数十种之多,其运动学位置逆解能否用统一的算法求解,一直是国内外机构学和机器人领域的研究目标.1980年,文献[1]最早尝试运用球面三角法进行统一求解,但最后剩下了 15种机构无法解决.1986年,文献[2]解决了喻为机构运动分析中的珠穆朗玛峰难题——7R机构位移分析以后,理论上完成了全部串联机构的位置逆解,但针对不同类型的串联机构进行数学建模时,将产生不同的数学模型,需要不同的消元技巧,难以实现计算机程序自动求解.2006年,文献[3]提出把串联运动链拆成几个简单部分的组合,但该方法只适于某些解耦的特殊情况.以往用于串联机构位置逆解数学建模的方法主要有D-H矩阵法、球面三角法、实矩阵法、对偶数法等,得到了各不相同的逆解算法,不具有通用性.究其原因,主要是缺乏有效的数学建模方法,不能将D-H矩阵中的旋转和平移统一表达,难以建立串联机构逆解统一数学模型.随着串联机器人模块化、可重构技术的发展,研究 6R串联机构位置逆解新方法,探索串联机构统一逆解建模及通用算法,具有重要的理论价值与实际意义.

倍四元数把刚体三维空间的旋转和平移统一为四维空间的纯转动,从而减少了机构的种类.文献[4]将三维空间中位移表示为四维空间中倍四元数表示的双旋转;文献[5]将倍四元数应用于运动插值中;文献[6]应用倍四元数对空间 RR机器人进行综合;文献[7]运用倍四元数完成了空间 6自由度串联机构位置逆解,但该方法在构造Dixon结式时,需要通过人工参与查找公因式来消除增根,未能实现该机构位置逆解的自动求解.

本文采用未知转角的复指数形式,改进了一种空间 6R串联机构位置逆解新算法.基于倍四元数建立了空间 6R串联机构位置逆解数学模型,构造了 6×6的 Dixon结式,新算法不需要提取任何公因式,可直接获得该机构位置逆解的一元 16次方程及其全部封闭解,方法简单实用,易于程序实现.

1 倍四元数形式的齐次变换矩阵

串联机构位置逆解数学建模通常采用 D-H矩阵法,相邻关节两坐标系 i-1和 i之间的关系,可通过图 1中各个参数来描述.

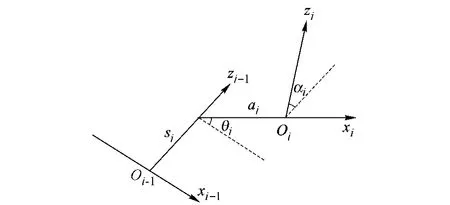
图1 D-H相邻坐标变换

图1表示坐标系 i-1绕自身 z轴旋转 θi且沿z轴平移 si后得到一新的坐标系;新坐标系再绕其自身 x轴旋转 αi且沿 x轴平移 ai后得到 i坐标系.其中,坐标系 i-1绕自身 z轴旋转 θi且沿 z轴平移 si的齐次变换矩阵,运用倍四元数可表示为[5]

其中

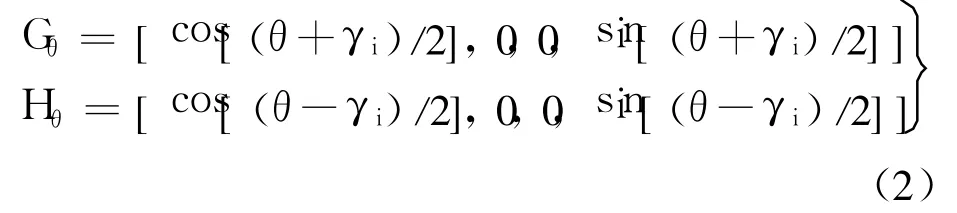
由式(1)可知,坐标系 i-1绕自身 z轴的旋转和平移变换,运用倍四元数可以近似表达为四维空间中旋转(θ+γ)角和(θ-γ)角的双旋转,从而将 D-H矩阵中的旋转和平移统一为四维空间的双旋转.

为便于运算,式(1)可表示为 Clifford代数形式:

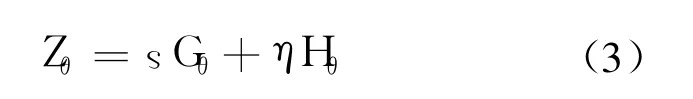
同理,坐标系绕其 x轴旋转角 αi且沿 x轴平移 ai的齐次变换矩阵用倍四元数形式表示为

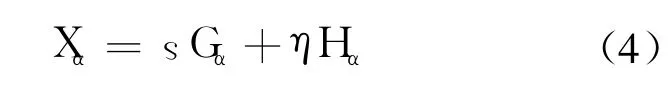
其中

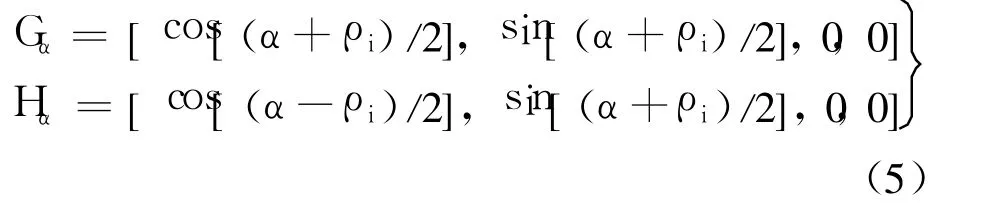
式中 ρi=ai/R.参考文献[5],R=L/δ1/2,其中 L为机器人手臂所能达到的空间尺寸的最大值,δ为指定的精度.

2 运动学位置逆解

2.1 数学建模

6R串联机构位置逆解就是已知操作臂的末端空间位姿和机构参数 si,ai,αi,求各关节的输入角 θi(i=1,2,…,6).6R串联机构有 6个关节,需要经过 6次图 1中的空间三维运动,运动学方程可表示为

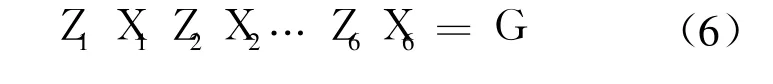
G为机器人操作末端位姿的倍四元数形式:

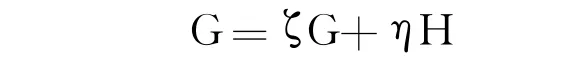
根据 Clifford代数运算法则[8],式(6)可以表示为

由式(7)和式 (8)得

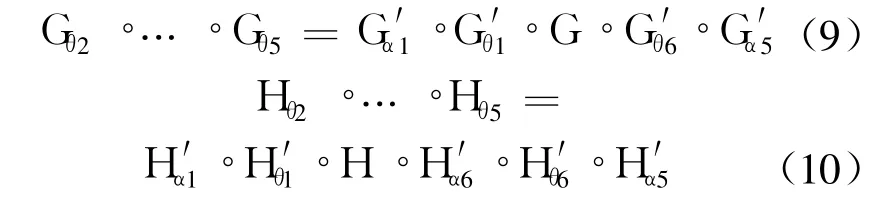
将式(2)、式 (5)代入式 (9)、式 (10),根据四元数各元素对应相等,得

其中,Ei为 4×16的矩阵;Di为 4×4的矩阵,其元素均为已知结构参数及输入参数确定;

2.2 消元过程

采用分步进行消元.首先,对式(11)(取 i=1)进行线性消元,消去 θ1和 θ6,并将其代入式(11)(取 i=2);然后运用 Dixon结式消去 θ3,θ4,θ5;最后得到关于 θ2的 ±8次单变量方程.

当 i=1时,将式(11)看做关于 c1c6,c1s6,s1c6,s1s6的线性方程组,得

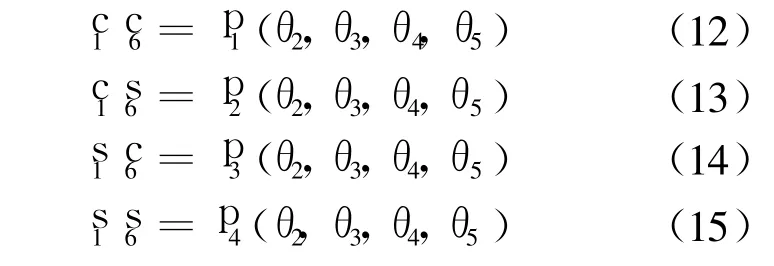
设 F0(t2,t3,t4,t5)=[f1,f2,f3,f4]T,对式(16)构造 Dixon结式如下:

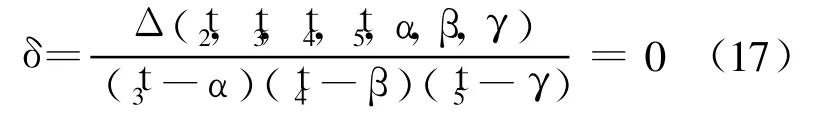
其中

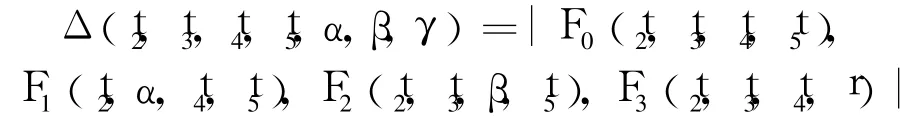
展开式(17)得

其中

矩阵 D6×6为一个只含变量 t2的 6×6方阵,即 Dixon矩阵.

由线性代数知识可知,式(18)成立的条件为

矩阵 D6×6每行分子分母关于变量 t2的最高次数为 1,2,1,1,2,1,其总和为 8.根据行列式的运算法则可知,展开式(18)后得到只含变量 t2的多项式分子分母最高次数不会超过 8.由式(19),不需要提取任何公因式,直接可得

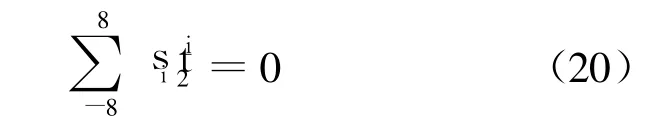
其中,si是由已知参数确定的系数.求解式(20)可得 t2的 16组解.

2.3 其它变量求解

将所求得的 16个 t2解代入下式:

根据 Cramer法测,可线性求解对应 t2的 t4和 t5.

将所求的 t2,t4和 t5代入式(16)中任一式,即可求得对应的 t3.从而求得 θ2,θ3,θ4,θ5,由式(12)～式(15)可求得 θ1和 θ6.

3 数值算例

采用本文的算法对文献[8]中的数值算例求解,其 6R串联机构的结构参数和位置参数如下:

表 1 数字实例的 4组实数解 (°)

4 结 论

1)将倍四元数的复指数形式应用于串联机构位置逆解分析中,得出 8个约束方程,通过线性变换和 Dixon结式获得了一元 16次方程及其及全部解析解,求解过程简洁,易于程序实现,为 6R串联机构位置逆解提供了新的算法.

2)倍四元数把三维空间的转动和移动统一为四维空间的纯转动,因此,本文提出的算法可适用于由转动副、移动副及圆柱副三种运动副组成的空间 6自由度串联机器人机构位置逆解.

References)

[1]Duffy J.Analysis of mechanisms and robot manipulators[M].London:Ed wart Arnold Ltd,1980

[2]廖启征,梁崇高,张启先.空间 7R机构位移分析的新研究[J].机械工程学报,1986,22(3):1-5 Liao Qizheng,Liang Chonggao,Zhang Qixian.New research of displacement analysis of spatial 7R mechanism[J].Chinese Journal of Mechanical Engineering,1986,22(3):1-5(in Chinese)

[3]赵杰,王卫忠,蔡鹤皋.可重构机器人封闭形式的运动学逆解计算[J].机械工程学报,2006,42(8):210-214 Zhao Jie,Wang Weizhong,Cai Hegao.Generation of closed-form inverse kinematics for reconfigurable robots[J].Chinese Journal of Mechanical Engineering,2006,42(8):210-214(in Chinese)

[4]Etzel K R,McCarthy JM.A metric for spatial displacement using biquaternions on SO(4)[C]//Proceedings of IEEE International Conference on Robotics and Automation.Piscataway,NJ:IEEE,1996:3185-3190

[5]Geng Q J,Varshney A,Menon JP,et al.Double quaternions for motion interpolation[C]//Proceedingsof the ASME DETC'98.Atlanta:ASME,1998:13-16

[6]McCarthy JM.Mechanismssynthesis theory and the design of robots[C]//Proceedings of IEEE International Conference on Robotics and Automation.San Francisco,CA:IEEE,2000:24-28

[7]乔曙光.6自由度串联机械手位置逆解新方法[D].北京:北京邮电大学自动化学院,2008 Qiao Shuguang.New algorithm for inverse kinematics of 6 DOF serial manipulator[D].Beijing:School of Automation,Beijing U-niversity of Posts and Telecommunications,2008(in Chinese)

[8]Clifford W K.A prelim inary sketch of biquaternions[G]//Tucker R.Mathematical Papers.London:London Mathematical Society,1882:658

[9]于艳秋,王品,廖启征.一般 6R机器人位置反解与运动仿真[J].中国机械工程,2003,14(24):2130-2132 Yu Yanqiu,Wang Pin,Liao Qizheng.Forward kinematics analysis of general 6R robot and its simulation[J].China Mechanical Engineering,2003,14(24):2130-2132(in Chinese)

(编 辑:文丽芳)

New algorithm for inverse kinematics of 6R serial robot mechanism

Huang Xiguang

(School of Mechanical and Electrical Engineering,North China University of Technology,Beijing 100041,China)

Liao Qizheng

(School of Automation,Beijing University of Posts and Telecommunications,Beijing 100876,China)

The theory of double quaternions and its application in the inverse kinematics of serial mechanisms was introduced.A new algorithm for the inverse kinematics of 6R mechanisms was presented based on the complex exponent form of double quaternions.Based on double quaternions,a mathematical model of 6R mechanisms was created.Then,a 6×6 resultant matrix was obtained directly by using linear elimination and Dixon resultant method,without factoring outor deriving the greatest common divisor,due to the proposed algorithm used the complex exponent form of double quaternions.A 16th degree univariate equation was achieved from the determinant of the matrix and all 16 closed-form solutions were also obtained.The proposed algorithm is comparably easy and simple to program.It was verified by a numerical example that the obtained roots satisfy the original equations.The research result provides a new method for the inverse kinematics of serial mechanisms.

serial mechanism;double quaternions;inverse kinematics

TH 112

A

1001-5965(2010)03-0295-04

2009-03-05

国家自然科学基金资助项目(50775012);北京市属院校人才强教计划资助项目;北京市特色专业建设资助项目;北方工业大学校科研基金资助项目

黄昔光(1979-),男,湖南岳阳人,讲师,huangxiguang@gmail.com.