基于 EMD与切片双谱的轴承故障诊断方法

张 琳 黄 敏

(北京航空航天大学 工程系统工程系,北京 100191)

基于 EMD与切片双谱的轴承故障诊断方法

张 琳 黄 敏

(北京航空航天大学 工程系统工程系,北京 100191)

针对轴承故障诊断问题,提出一种基于经验模态分解(EMD,Empirical Mode Decomposition)与切片双谱分析相结合的新方法.将原始信号分解成不同尺度的固有模态函数(IMF,Intrinsic Mode Function),求取 IMF分量的包络,计算其对角切片双谱,提取由于二次相位耦合产生的非线性特征,得到轴承的故障特征频率.通过对仿真信号进行分析,表明该方法克服了传统的基于EMD的包络功率谱方法不能抑制噪声的缺点,同时较传统高阶谱方法计算量更小.给出了 6205-2RS JEM SKF轴承诊断实例,说明了该方法的可用性.

故障诊断;轴承;EMD;切片双谱

基于经验模态分解(EMD,Empirical Mode Decomposition)的时频分析方法是 1998年 Norden E.Huang等人创立的一种时频信号分析方法[1-3],尤其适用于非线性、非稳态的信号序列处理.同时,该方法可自适应地提取故障冲击信号,避免了共振解调中心频率选择和多个固有频率共存的问题;此外,与小波分析技术相比,该方法不存在难于选取小波函数的问题,表现出更强的易用性.

高阶谱分析技术[4-6]是近年来信号处理的新技术,是对非高斯、非线性、非因果信号处理和高斯噪声处理非常有用的分析工具,在理论上可以完全抑制噪声的影响,提高分析和辨识精度,同时更容易获得相位信息.

传统的基于 EMD的轴承故障诊断方法大多是利用包络的功率谱分析技术来实现的[7],但是,功率谱方法不能够抑制噪声对 EMD方法的影响,使得 EMD在工程中的使用受到了很大局限.为此,本文引入了切片双谱方法,提出了基于EMD与切片双谱的轴承故障诊断方法.

1 EMD方法的基本原理

EMD方法[1]的目的是通过对非线性、非平稳信号的分解获得一系列表征信号特征时间尺度的固有模态函数(IMF,Intrinsic Mode Function),使得各个 IMF是单分量的幅值或频率调制信号.IMF要满足 2个条件:①整个数据序列的极值点与过零点的个数相等或最多相差一个;②在任意时刻,由局部极大值点形成的上包络与由局部极小值点形成的下包络的均值为零.这 2个条件实际上使得分解得到的 IMF是窄带信号.同时,EMD分解方法还建立在以下假设上:①信号至少有 2个极点,一个最大值和一个最小值;②特征时间尺度通过 2个极值点之间的时间定义;③若数据缺乏极值点但有形变点,则可通过微分数据一次或几次获得极值点,然后再通过积分来获得分解结果.

对任意一个实信号 x(t)进行 EMD的具体步骤是:

1)确定 x(t)上的所有极大值点和极小值点;然后,将所有极大值点和所有极小值点分别用三次样条曲线连接起来,将这两条曲线分别作为 x(t)的上下包络线.计算出它们的平均值曲线m1(t),用 x(t)减去 m1(t)得

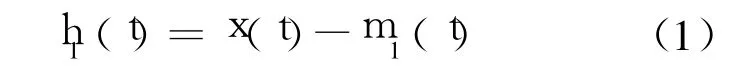
如果 h1(t)不满足 IMF的条件,需要把 h1(t)作为原信号重复上面的步骤得到 h11(t)

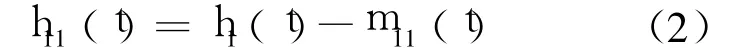
筛选 k次直到 h1k(t)变为一个 IMF,即

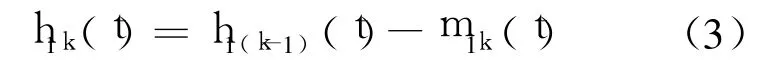
这样就从原信号中分解出了第一个 IMF,称为第一阶 IMF,记作

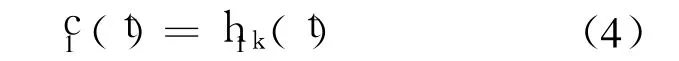
2)从原信号中减去 c1(t)得第一阶剩余信号r1(t)

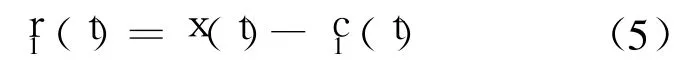
由于第一阶剩余信号 r1(t)还包含着更长周期的分量,因此,把 r1(t)作为新的原信号,重复步骤 1,对后面的也进行同样的筛选,这样依次分解得到

直至剩余信号 rn(t)中的信息对所研究内容意义很小,或者变成一个单调函数不能再筛选出基本模式分量为止.至此,信号 x(t)已被分解成 n个基本模式分量 ci(t)和一个剩余信号 rn(t).这样,由式(5)和式(6)得到:

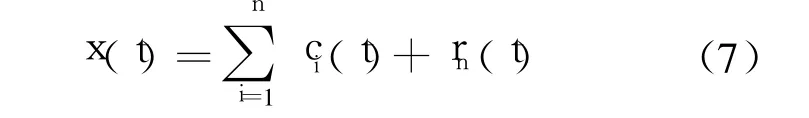
进一步,各个 IMF分量可通过 Hilbert变换进行包络解调.

但是,由于所分析信号的有限长度、信号的两端点不能确定是极点,那么,在进行三次样条插值的时候,必然使得信号的上下包络在信号的两端附近严重扭曲,即产生端点效应.本文使用了文献[8]中的极值点对称延拓法来处理该问题.

2 双谱分析

2.1 双谱的概念

高阶谱分析技术[4]是现代信号处理的新技术,与功率谱相比具有如下特点:①功率谱是实数,不包含相位信息,而高阶谱是复数,因而保留了相位信息;②能抑制噪声的影响;③保留了系统的非线性信息.因此,用高阶谱分析振动信号更容易获得特征信息.

定义零均值平稳随机过程 x(t),其三阶累积量为

相应的累积量谱定义为 x(t)的 k阶累积量的 k-1维傅里叶变换,则三阶谱定义为双谱:

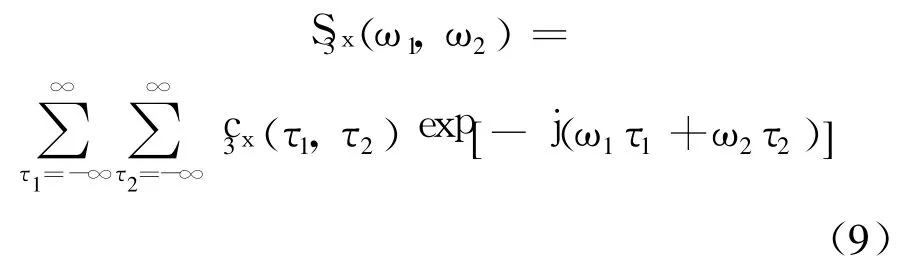
2.2 切片双谱检测二次相位耦合现象

当机械系统发生故障时,系统往往表现出较强的非线性,产生二次相位耦合现象.对于这种非线性耦合现象,仅用二阶统计信息如功率谱是很难从根本上解决问题的,而双谱则可以定量描述二次相位耦合[5].但是用双谱计算二次相位耦合计算量大,不便于定量分析且二维图不够直观.

当轴承发生故障时,采样信号的特征为受干扰的冲击调制信号,即

式中,ωi为调制源(包括轴承故障特征频率及其谐波频率);ω0为载波频率;b为任意常数.因此故障轴承振动信号解调后的信号包含了故障特征频率的一簇谐波,且相位是互相关联的,即存在二次相位耦合现象[5].若设 ωF为轴承的故障特征频率,则双谱的(ωF,ωF)处必然出现相位耦合现象,从而双谱在(ωF,ωF)处会有明显的谱峰.

根据以上分析,本文将切片双谱分析引入轴承的故障诊断方法之中,即记 ω1=ω2=ω,则对角切片双谱估计为.当 ω=ωF时,必然出现明显的峰值,将峰值对应的频率与理论计算的轴承的故障特征频率相比较,就可以得出正确的结论,同时减小计算量,增强频谱图的可视性.

3 切片双谱抑制噪声对 EMD影响

一般情况下,轴承的故障振动信号都带有大量高斯噪声,而传统的功率谱分析方法不能抑制高斯噪声对 EMD方法的影响.考察如下仿真信号:

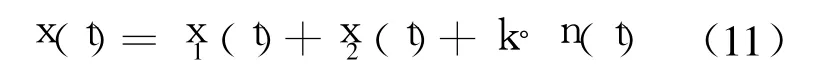
其中

n(t)为功率是 1的高斯白噪声;k为调节噪声大小的常数.图 1为无噪声时,即 k=0时信号 x(t)经 EMD分解得到的前 2个 IMF分量的包络功率谱.此时,可以清晰地观察到包络谱在 30Hz和10Hz,即相应调制频率 2倍处有明显的峰值,可以很好地分辨出调制频率.图 2为 k=3,信噪比为 1:18时信号 x(t)经 EMD分解得到的前 2个IMF分量的包络功率谱.此时,IMF包络谱在噪声的干扰下已经失去了意义.图 3为无噪声时,即k=0时 x(t)的前 2个 IMF分量的包络切片双谱图,从中可以观察到切片双谱在 15Hz和 5Hz,即相应调制频率处有明显峰值,可以很好地分辨出调制频率.图 4为 k=3,信噪比为 1:18时 x(t)的前 2个 IMF分量的包络切片双谱图,此时,仍然可以清楚的观察到 15Hz和 5Hz 2处的峰值.

以上分析说明,切片双谱可以有效抑制噪声对 EMD方法的干扰.这是因为高斯白噪声的功率谱密度在整个频域是均匀分布的,EMD对高斯白噪声来说是一个二分滤波器组,分解所得的每一IMF分量都服从高斯分布,且其 IMF的能量谱与相应的平均周期之积是一个常数;而且EMD分解所得的 IMF分量的平均频率是严格从高到低排列的;因此,它会影响到所有的 IMF分量,并且对IMF分量的影响是从高到低逐渐减弱的.而对于零均值的高斯过程,其三阶累积量和双谱为零,切片双谱作为双谱的一种特例,其值也为零[3].在机械故障诊断中,故障信号常常是非高斯的,非故障信号往往是高斯的,因此通过切片双谱分析,可以降低高斯噪声的影响,更好地将EMD方法应用于工程之中.

图1 无噪声时 x(t)前 2个 IMF分量的包络功率谱

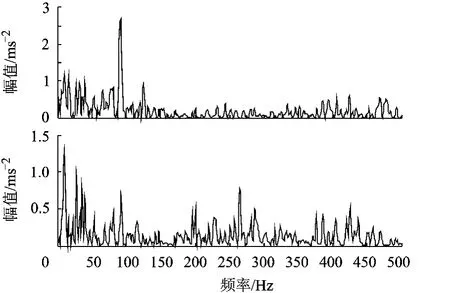
图2 k=3时 x(t)的前 2个 IMF分量的包络功率谱

图3 无噪声时x(t)前 2个 IMF分量的包络切片双谱

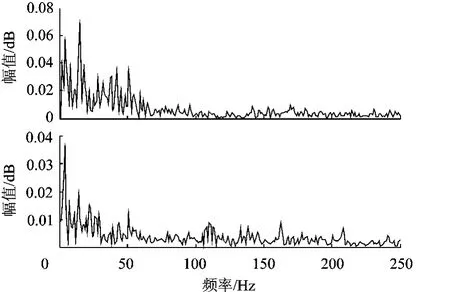
图4 k=3时 x(t)前 2个 IMF分量的包络切片双谱

4 轴承故障诊断实例

此数据来自华盛顿天主教大学轴承数据中心(http://www.eecs.case.edu/laboratory/bearing/apparatus.htm).测试实验台由一个 1491W的电机,一个扭矩传感器/编码器,一个功率计和控制电路组成,选用 6205-2RS JEM SKF轴承进行测试,利用电蚀加工在测试轴承内圈引入单点故障,故障直径为 0.1778mm,故障频率为 129.9648Hz.

振动数据被用连接在磁基外壳上的一个加速度传感器收集.加速度传感器被安装在电机外壳上驱动端和风扇端的 12点方向位置.振动信号用一个 16通道的 DAT记录仪收集,在 Matlab环境下做进一步处理,使所有数据保存为 Matlab文件格式(*.mat).采样数据为驱动端轴承数据,采样频率为 12000Hz,电机转速为 1772 r/min.

本文中使用 Matlab编程实现,首先对原始振动信号进行零均值化处理,并实施 EMD分解,对分解后 IMF分量进行包络解调,最后利用对角切片双谱分析提取轴承的故障特征.具体流程如图5所示.

图5 基于EMD与切片双谱的振动信号处理流程

图6为故障轴承利用上述方法得到的切片双谱图.该图显示,当轴承存在内圈存在点蚀时,最终得到的对角切片双谱在频率 130Hz处有明显的谱峰存在,这与数据中心提供的故障频率一致.

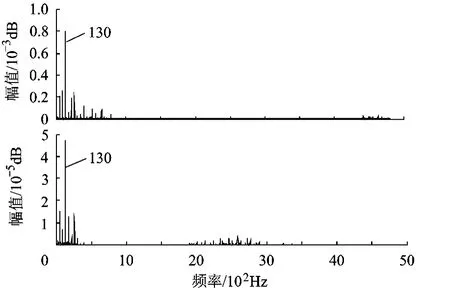
图6 内圈振动信号前 2个IMF分量的包络切片双谱

5 结 论

本文将切片双谱分析引入了轴承的故障诊断,提出了一种基于 EMD与切片双谱的轴承故障诊断方法.通过对实例验证分析,得出如下结论:①切片双谱方法将双谱的二维函数计算转换为一维函数,减小了谱分析的计算量,同时增强了二维谱图的可视性.②切片双谱可以有效抑制噪声对EMD方法的干扰,对于低信噪比的振动信号,亦可准确有效地提取故障信息.因此通过切片双谱分析,可以更好的将 EMD方法应用于工程之中.③该方法将 EMD与切片双谱相结合,用以提取由于二次相位耦合产生的非线性特征,能较准确地提取到轴承的故障特征频率.

References)

[1]Huang Norden E,Shen Zheng,Long Steven R,et al.The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc R Soc lond A,1998,454:903-995

[2]Huang Norden E,Shen Zheng,Long Steven R.A new view of nonlinear water waves:the hilbert spectrum[J].Annu,Rev Fluid Mech,1999,31:417-457

[3]Huang Norden E,Wu Man-Li C,Long Steven R,et al.A confidence lim it for the empirical mode decomposition and hilbert spectral analysis[J].Proc R Soc Lond 2003,A 459:2317-2345

[4]吴国正,夏立,尹为民.现代信号处理技术[M].武汉:武汉大学出版社,2003:15-29 Wu Guozheng,Xia li,Yin Weimin.Modern signal processing technology[M].Wuhan:Wuhan University Press,2003:15-29(in Chinese)

[5]Raghuveer M R.Time-domain approaches to quadratic phase coupling estimation[J].IEEE Transaction on Automatic Control,1990,35:48-56

[6]Zhang Guicai,Du Ruxu,Shi Tielin.Extracting gear fault features using integrated bispectrum[C]//International Conference on Robotics,Intelligent Systems and Signal Processing.Changsha:IEEE,2003:548-553

[7]李辉,郑海起,唐力伟.基于 EMD和包络谱分析的轴承故障诊断研究[J].河北工业大学学报,2005,34(2):12-15 Li Hui,Zheng Haiqi,Tang Liwei.Study on faults diagnosis of bearing based on EMD and envelope spectrum[J].Journal of Hebei University of Technology,2005,34(2):12-15(in Chinese)

[8]舒忠平,杨智春.抑制经验模分解边缘效应的极值点对称延拓法[J].西北工业大学学报,2006,24(5):639-643 Shu Zhongping,Yang Zhichun.A better method for effectively suppressing end effect of empirical mode decomposition(EMD)[J].Journal of Northwestern Polytechnical University,2006,24(5):639-643(in Chinese)

(编 辑 :娄 嘉)

Fault diagnosis approach for bearing based on EMD and slice bi-spectrum

Zhang Lin Huang Min

(Dept.of System Engineering of Engineering Technology,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

A new approach based on the empirical mode decomposition(EMD)and slice bi-spectrum was presented for fault diagnosis on roller bearings.Original signals were decomposed into a series of intrinsic mode functions(IMFs)of different scales.Envelopes of the IMFs were extracted and a diagonal slice bi-spectrum for the envelopes was computed to extract the non-linear feature deriving from the quadratic phase coupling,as well as the fault characteristic frequencies.An analysis on simulation signals shows that the drawback that traditional envelope spectrum methods based on EMD cannot inhibit the noise can be overcome by this approach.Meanwhile,its computation load is less than traditional high-order spectrum methods.A diagnosis instance of the bearing 6205-2RS JEM SKFwas presented to show the feasibility of this approach.

fault diagnosis;bearings;empirical mode decomposition;slice bi-spectrum

TH 133.33

A

1001-5965(2010)03-0287-04

2009-03-04

张 琳(1984-),女,天津人,硕士生,zl@dse.buaa.edu.cn.