舵面电动加载系统的自适应 CMAC复合控制
2010-03-16杨波王哲
杨 波 王 哲
(北京航空航天大学 自动化科学与电气工程学院,北京 100191)
舵面电动加载系统的自适应 CMAC复合控制
杨 波 王 哲
(北京航空航天大学 自动化科学与电气工程学院,北京 100191)
针对无人机舵面电动加载系统具有非线性及多余力矩的特点,提出了一种自适应 CMAC(Cerebellar Model Articulation Controller)神经网络与自适应神经元控制器并联构成复合控制结构.该控制策略以系统的指令输入和实际输出作为 CMAC的激励信号,以系统的当前控制误差作为 CMAC的训练信号.提出了利用误差在线自适应调整学习率的方法,消除了常规前馈型 CMAC的过学习和不稳定现象.建立了无人机舵面电动加载系统的数学模型,给出了具体的控制结构和算法.仿真结果表明:该方法有效抑制了加载系统的多余力矩,增强了系统的稳定性,明显改善了舵面电动加载系统的动态性能.
舵面电动加载系统;多余力矩;小脑模型关联控制器神经网络;自适应控制;自适应神经元;学习率
舵面电动加载系统用于实验室条件下无人机舵机的负载模拟试验,以检测和考核舵机系统在实际负载条件下的控制律、动态性能、系统可靠性等.对于无人机而言,舵面载荷相对较小,所以通常采用电动加载系统.
舵面电动加载系统存在着由于被加载系统的主动运动引起的多余力矩.多余力矩会影响加载系统的控制精度、带宽和稳定性,因此如何抑制乃至消除多余力矩是舵面电动加载系统必须解决的关键问题.工程中通常采用结构不变性原理来抑制多余力矩,但在实际的舵面电动加载系统中,存在非线性(如摩擦、机械连接间隙等)以及参数变化问题,采用该方法往往达不到理想效果[1].
小脑模型关联控制器(CMAC,Cerebellar Model Articulation Controller)是一种采用局部学习结构的神经网络,具有结构简单、有一定的泛化能力和学习速度快等优点,适合于实时控制.但CMAC网络结构的设计目前理论指导较少,这给其设计和推广带来了难度.目前常用的是 CMAC的前馈控制和固定增益反馈 PD(Proportional-Derivative)控制器相结合的复合控制,但在跟踪连续变化的信号时,误差累积的影响会使 CMAC产生过学习现象,导致系统不稳定[2].基于 CMAC的控制系统稳定性与学习率取值密切相关,如学习率选取不当,会导致控制系统不稳定或者收敛速度很慢[3].而固定增益反馈控制器的大小也影响着系统的稳定性和抗干扰能力[4].文献[5]提出了采用线性神经元控制器实现固定增益的自适应调节,使系统的品质得到了改善.
本文根据舵面电动加载系统的实际应用情况,提出了一种基于 CMAC神经网络的自适应控制器,仿真结果表明了本方法的有效性.
1 舵面电动加载系统数学模型
为尽可能真实模拟飞机舵面在不同飞行任务中承受的载荷情况,舵面电动加载系统往往是多通道并行系统,由于各通道之间彼此独立,因此对单通道加载系统进行数学建模.力矩电机作为主要载荷模拟设备,通过联轴器与力矩传感器相连,再通过摇臂、拉杆和舵机摇臂将载荷施加到舵机轴上.
舵面电动加载系统是以转矩为被控量的直流电机伺服系统,采用脉冲宽度调制驱动装置,产生大功率电流驱动直流力矩电机对被加载对象加载,加载系统通过连接机构与承载舵机相连,对其加载并随之在一定角度内进行往复运动[6].
直流电机的电压平衡方程为
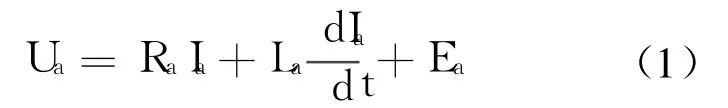
电机反电势为

其中

电磁转矩可表示为

电机转矩为
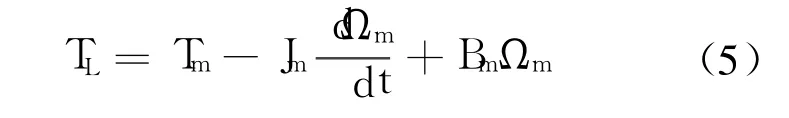
式中,Ua,Ea,Ia分别为力矩电机电枢电压、反电动势和电枢电流;KE,KT分别为力矩电机的反电动势系数和转矩系数;Ra,La分别为电枢的电阻和电感;Ωm,θm分别为电机的角速度和角位移;Bm,Jm分别为电机的转矩系数和转动惯量.
由式(1)~式(5),可得电机的传递函数:

不考虑转矩传感器的扭转刚度,认为电机轴和负载是刚性连接,承载对象可看成是惯性负载,其粘性阻尼系数近似为零.
系统的力矩平衡方程如下:
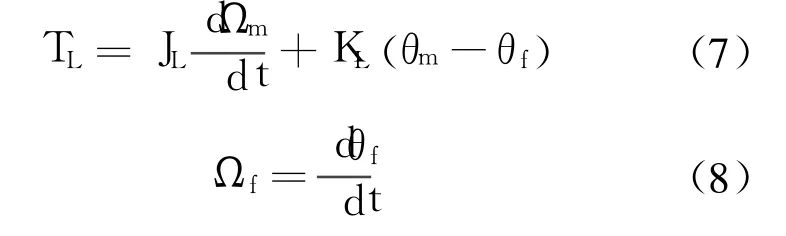
式中,JL为被加载对象端负载的转动惯量;KL为被加载对象端负载的扭转刚度;Ωf为被加载对象端的角速度;θf为被加载对象端的角位移.联立式(6)~式(8)可得加载系统的传递函数:
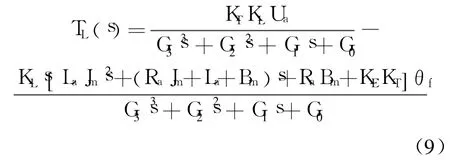
其中

由式(9)可以看出分子第 2项实际上是强位置干扰量产生的力矩,即所谓的多余力矩.
2 自适应 CMAC控制器
2.1 自适应 CMAC结构和算法
CMAC-PD复合控制器通过 CMAC实现前馈控制,确保系统的响应速度,减少超调量.常规 PD算法实现反馈控制,以保证系统的稳定性,抑制扰动.
通过仿真实验发现,传统的 CMAC-PD控制,系统在维持相当长时间的稳定后,会产生过学习现象导致突然崩溃.为了提高系统的稳定性和抗干扰能力,对 CMAC神经网络控制器的结构进行了改进,改进后的结构如图 1所示.
该控制器与常用的前馈-反馈复合控制结构类似,但它采用二维输入,以系统的给定信号r(k)和实际输出信号 y(k)作为 CMAC的输入.

图1 自适应 CMAC神经网络复合控制器结构
常规的复合控制采用 PID(Proportional Integral Differential)控制器的输出作为调整权值学习的训练信号,CMAC学习的是被控对象的逆动态模型.而改进后的复合 CMAC-PD控制结构采用的是系统的跟踪误差 e(k)作为调整权值学习的训练信号,因此 CMAC实现的不仅仅是被控对象的逆动态模型,而且是包括了常规反馈控制器在内的整个系统的逆动态模型.另外在学习算法中,本文提出了一种变学习率的方法,根据误差的大小进行自适应在线调节,可以有效地消除传统的控制结构中,由于 PD控制器和 CMAC在学习中产生冲突,导致系统不稳定的现象.为了进一步提高系统的控制精度和稳定性,用自适应神经元控制器取代常规的 PD固定增益控制器,它能根据控制系统的动态特性优化 CMAC的自学习控制,使其能适应各种系统工况的变化,从而提高系统的控制品质.
基于 CMAC自适应控制器的控制算法如下:
1)设置联想单元个数、泛化参数和量化参数;
2)初始化参数,CMAC联想单元的权值均为零;
3)根据式(14)对 r(k)和 y(k)进行量化:

式中,round为取整函数;xmax和 xmin分别为输入 x的最大值和最小值;M为 xmax对应的量化值;
4)在 CMAC中找到与之对应的 C个单元,并将这 C个单元的权值相加,得到 CMAC的输出:
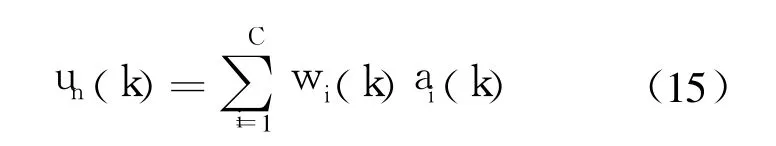
式中,wi(k)为 CMAC第 k次的权值;ai(k)为二进制选择向量;C为 CMAC网络的泛化常数;
5)将 CMAC输出值和自适应网络神经元控制器的输出 un(k)相加,得到被控对象总的控制输入,即

6)用 e(k)作为训练信号,调整联想单元中的权值大小,进入学习过程,权值调整规则为
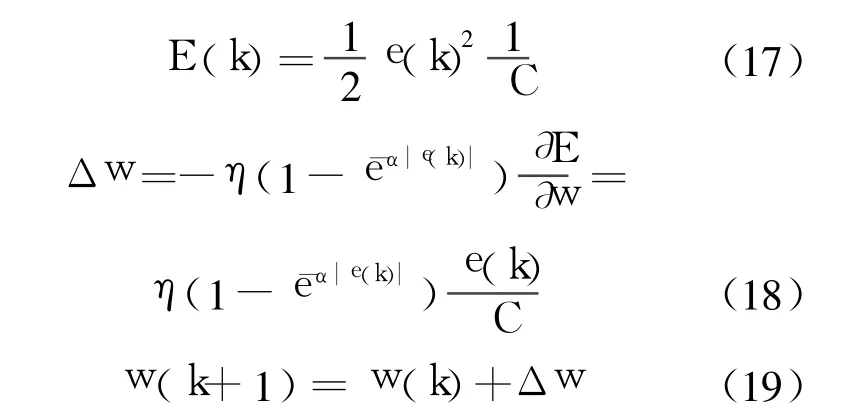
式中,η(1-e-α|e(k)|)为改进后的 CMAC神经网络的学习率,η为常数且 η∈(0,1),1-e-α|e(k)|为学习率比例因子.η(1-e-α|e(k)|)随着 e(k)的减小呈指数衰减,当 e(k)较小时,较小的 η(1-e-α|e(k)|)可以抑制累积误差的影响所导致系统的不稳定性,而 e(k)较大时,较大的 η(1-e-α|e(k)|)可以加速系统的收敛.α为平衡常数,用来协调系统的稳定性和收敛速度.对于常规CMAC而言,固定学习率无法解决稳定性和收敛速度之间的矛盾,而改进后的算法可以根据系统e(k)大小在学习过程中动态地调整 η(1-e-α|e(k)|),从而提高了系统的自适应性,有效地增强了系统的稳定性;
7)k=k+1,转3).
2.2 自适应线性神经元控制器设计
常规 CMAC复合控制中的 PID控制采用传统的 PD算法而不是 PID算法,目的是使 CMAC的学习仅依赖于误差当时的测量值及变化值.为不改变原有常规固定增益控制器的结构,自适应线性神经元控制器的具体结构如图 2所示.

图2 自适应线性神经元结构
控制器的输出为

式中,w1(k)和 w2(k)为神经元的权重,分别对应常规 PD控制器的比例和微分调节系数 Kp和 Kd;x1(k)和 x2(k)为神经元输入信号,分别对应给定的误差和误差变化量.取性能指标函数:

用梯度下降法来修正网络的权系数,即按E(k)对加权系数的负梯度方向搜索调整:
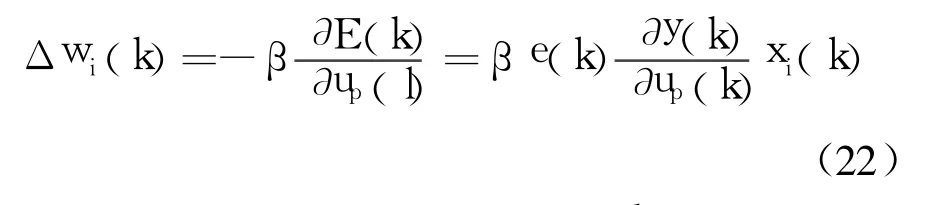

综上所述,本文提出的复合控制通过学习率自适应调整的 CMAC来协调系统动态性能和稳态性能之间的矛盾,它与自适应神经元控制器一同提高了系统的稳定性和抗干扰能力,从而改善了系统的控制性能.
3 仿真结果及分析
为了验证自适应 CMAC控制器控制策略的有效性,需要进行对比仿真分析.将舵面电动加载系统的相关参数 Jm=0.01kg·m2,La=4.3mH,Ra=3.5Ω,KT=1.754 N· m/A,KE=2.046 V/(r·min-1)等参数代入式(9),其中常规固定增益 PD控制器参数设定为 Kp=2,Kd=0.5;CMAC的参数设定为 w1(0)=2,w2(0)=0.5,η=0.05,α=1,C=20,给定信号和实际输出信号的量化级数 N均取 100.自适应神经元的学习速率为 β=0.001.取舵机的角速度干扰信号 yr=1.74sin(5· 2πt)rad时,未加 CMAC时多余力矩的峰值为 1.86N·m.
下面分别针对结构不变性控制,CMAC与常规固定增益 PD复合控制以及本文提出的自适应CMAC复合控制进行仿真比较.
3.1 正弦波信号的跟踪性能仿真
取加载指令为 r(k)=10 sin(10· 2πt)N·m,对于无人机舵面电动加载系统而言,加载指令的频率已为极限值,仿真时间取 2s.图 3为采用结构不变性控制的仿真结果,|e(k)|幅值为1.3N·m;图 4为 CMAC与常规 PD复合控制,图5为自适应 CMAC控制,0.5 s后,|e(k)|幅值均收敛到 0.5 N·m左右.由此可见,采用基于CMAC控制策略的效果明显优于结构不变性控制效果,多余力矩减小了 60%,从图中可以看出,采用自适应 CMAC后,系统也能迅速收敛,且多余力矩等干扰对系统误差的影响只有 5%.

图3 基于结构不变性原理跟踪曲线

图4 基于 CMAC与常规 PD复合控制跟踪曲线

图5 基于自适应CMAC复合控制跟踪曲线
3.2 CMAC复合控制稳定性仿真
针对 CMAC和 PD复合控制相互作用,可能经过相当长的稳定时间,最终导致系统发散的问题,有必要测试其稳定性.
正弦波信号的取值同 3.1,将仿真时间延长为 500s,图 6为常规 CMAC和固定增益 PD复合控制的仿真结果.可见虽然系统一开始能够迅速收敛,但经过 85s后,就出现发散现象,而图 7采用的自适应 CMAC复合控制在经过 500 s仿真后,|e(k)|幅值仍保持在0.4N·m左右,没有发散的趋势.由此可见本文提出的自适应控制器,通过自适应神经元 KP,Kd以及 CMAC控制部分学习率的在线调整,不仅使系统具有良好的动态响应性能和跟踪连续变化信号的能力,而且有效地提高了系统的稳定性.

图6 100s常规 CMAC和固定增益PD复合控制跟踪误差
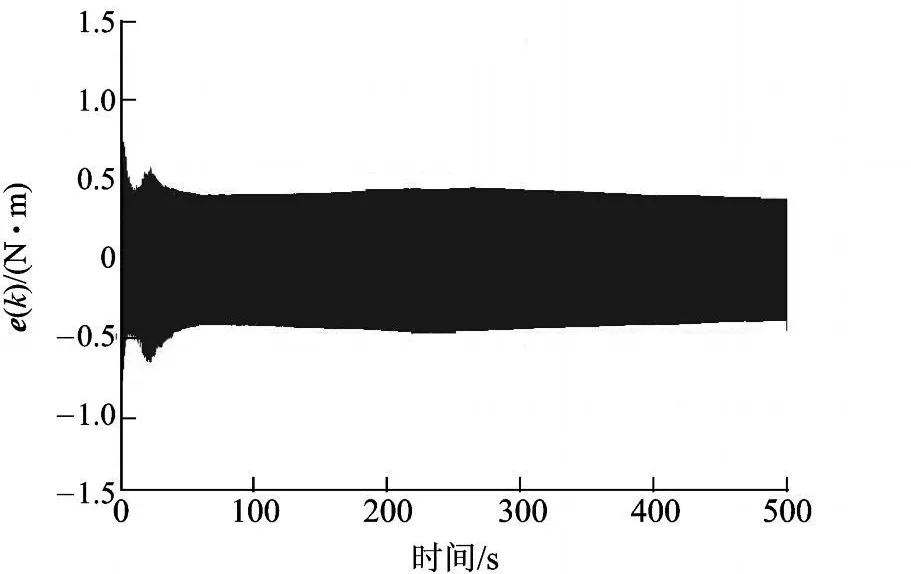
图7 500s自适应CMAC复合控制跟踪误差
另外,为了验证本文提出的变学习率公式对于系统稳定性的作用,将 1-e-α|e(k)|取为 1,η=0.05即为固定学习率,其他参数均保持不变,仿真结果如图 8所示.虽然 500 s时由于自适应神经元控制器的作用使得系统并没有崩溃,但它有发散的趋势,而且时间一长对多余力矩的抑制效果不如图 7稳定.可见学习率的大小对系统的稳定也起着很重要的作用,固定学习率时有时并不能达到理想的效果,而变学习率在线调整权值增强了系统的自适应能力,它与自适应神经元一起有效地提高了系统的稳定性.
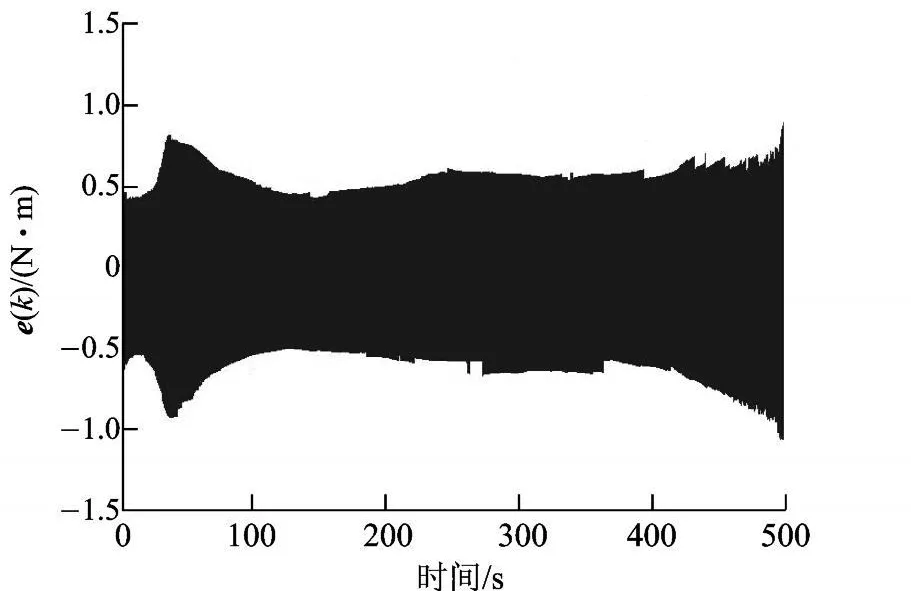
图8 500s固定学习率的自适应CMAC复合控制跟踪误差
4 结 论
多余力矩严重影响舵面电动加载系统的动态加载性能,仅采用结构不变性原理抑制多余力矩达不到理想的效果.本文针对无人机舵面电动加载系统的特点,在常规 CMAC复合控制的基础上,提出了一种自适应 CMAC神经网络控制器,该控制器以给定信号和实际输出信号为 CMAC的激励信号,以系统误差作为训练信号,在线调整学习率的大小并与自适应神经网络控制器相结合构成系统的复合控制.仿真结果表明:该方法既弥补了结构不变性原理的不足,明显抑制了多余力矩,又能保证系统的长期稳定性,从而有效地改善了系统的动态加载性能.相比于其他类型的神经网络控制,计算量小,非常适合于在线实时控制,对舵面电动加载系统的设计具有很大的参考价值.
References)
[1]任志婷,焦宗夏.小转矩电动式负载模拟器的设计[J].北京航空航天大学学报,2003,29(1):91-94 Ren Zhiting,Jiao Zongxia.Design of motor-drive load simulator with smalltorque outputs[J].Journal of Beijing University of Aeronautics and Astronautics,2003,29(1):91-94(in Chinese)
[2]蒋志明,林廷圻,黄先祥.一种基于 CMAC的自学习控制器[J].自动化学报,2000,26(4):542-545 Jiang Zhiming,Lin Tingqi,Huang Xianxiang.A new self-learning controller based on CMAC neural network[J].Acta Automatica Sinica,2000,26(4):542-545(in Chinese)
[3]林旭梅,梅涛.一种基于自适应遗传算法的 CMAC的学习率优化研究[J].系统仿真学报,2005,17(12):3081-3088 Lin Xumei,Mei Tao.A kind of optimization based on adaptive GA for cerebellar model articulation[J].Journal of System Simulation,2005,17(12):3081-3088(in Chinese)
[4]何超,徐立新,张宇河.CMAC算法收敛性分析及泛化能力研究[J].控制与决策,2001,16(5):523-529 He Chao,Xu Lixin,Zhang Yuhe.Convergence and generalization ability of CMAC[J].Control and Decision,2001,16(5):523-529(in Chinese)
[5]李辉.一种自适应 CMAC神经网络控制器的设计与仿真[J].2005,17(9):2233-2235 Li Hui.Design and simulation of adaptive CMAC controller[J].2005,17(9):2233-2235(in Chinese)
[6]杨波,王俊奎.基于改进的 CMAC的电动加载系统复合控制[J].航空学报,2008,29(5):1315-1318 Yang Bo,Wang Junkui.Hybrid control based on improved CMAC for motor-driven loading system[J].Acta Aeronautica et Astronautica Sinica,2008,29(5):1315-1318(in Chinese)
(编 辑:刘登敏)
Adaptive CMAC hybrid control for rudder electric loading system s
Yang Bo Wang Zhe
(School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Aiming at the nonlinearity and the surplus torque in rudder electric loading systems of unmanned aerial vehicle(UAV),aself-adaptive cerebellar modelarticulation controller(CMAC)was proposed,which was parallel to an adaptive neuron controller.This hybrid control strategy adopted the desired value and the actual out put as the incentive signals of CMAC,and put the current system error as the training signal of CMAC.The method was proposed by using the error to adjust the learning rate on line,which eliminated the excess self-learning phenomena.The mathematical model of rudder electric loading systems for UAV was established and the detailed control structure was put forward.Simulation results show that the proposed hybrid controller can effectively eliminate the surplus torque,enhance the control stability of the systems and fairly improve the dynamic loading performances of the systems,which is highly suitable for real-time control of nonlinear systems.
rudderelectric loading systems;surplus torque;neural cerebellar model articulation controller network;self-adaptive control;self-adaptive neurons;learning rate
TP 273
A
1001-5965(2010)03-0333-05
2009-03-02
杨 波(1972-),女,四川广安人,副教授,boyang@buaa.edu.cn.
