二萘嵌苯二酰亚胺衍生物的半导体性质

蔡 雪 齐冬冬 张跃兴 边永忠 姜建壮,*

(1北京科技大学化学系,北京 100083;2牡丹江师范学院化学系,黑龙江牡丹江 157012)

Organic field effect transistors(OFETs)have attracted increasing research interests[1]due to their great potential applications in the field of low-cost electronic devices,integrated circuits,and flexibledisplayssincetheirfirstreportin1986[2].Perylene diimide (PDI)semiconductors have been among the most intensively studied semiconductor materials.In recent years,the synthesis of n-type PDI-based organic semiconductors with good OFET performance has achieved great progress.Air-stable n-channel organicsemiconductorbasedona substituted perylene core(PDI-8CN2)wasreported[3].Twon-channelperylenediimide derivatives without strong electron-withdrawing groups have been studied[4]. The charge carrier mobility of PBI-F2and PBI-F4single crystalbased OFETs were revealed to reach up to 0.34 and 0.032 cm2· V-1·s-1[5].Two core-cyanated PDI derivatived,PDI-CN2and PDIFCN2,also exhibited air-stable n-type OFET carrier mobilities[6].

In addition to the intensive experimental studies over the preparation and fabrication of OFETs,theoretical and computational efforts have been paid to these perylene diimide semiconductors.For example,the semiconducting properties of N-fluoroalkylated dicyanoperylene-3,4∶9,10-bis(dicaboximides)(PDIFCN2)were investigated using DFT method[7].

In the present paper,as an extension of our research interests in OFETs[8-11],the charge transfer properties of chlorobenzyl or fluorobenzyl substituted PDI derivatives in crystal were investigated using density functional theory(DFT)calculations.The transfr integral in all the possible dimers composed of two neighboring PDI molecules for 1-4 is also studied.

1 Computational method and details

According to Marcus theory,the charge transfer can be described as a self-exchange electron-transfer reaction between a neutral molecule and a neighboring cation or anion.The holetransfer or electron-transfer process between spatially neighboring separated molecules can be represented by either of the following reactions:

where M represents neutral molecule undergoing charge transfer,and M+or M-means cation or anion,respectively.In this situation,the charge transport can be described as a sequential electron hopping process between consecutive molecules.As a result,the hoping rate(Wi)can then be modeled by classical Marcus theory:

where λ±is the reorganization energy,V the transfer integral,i a specific transfer pathway,kBthe Boltzmann constant,ħ Planck constant,and T the temperature.

The reorganization energy λ+or λ-for hole or electron transfer,respectively,which is not dependent on the relative positions of neighboring molecules,is calculated as the sum of the relaxation energies for neutral and positive radicals.The higher the reorganization energy is,the slower the hopping rates are. The reorganization energy λ+(λ-)is due to geometric relaxation accompanying charge transfer.The internal reorganization energies λ±can be defined as shown in Fig.S1(Supporting Information).

The transfer integral V depends on the relative arrangement of the molecules in the solid state and describes the intermolecular transfer integral,which needs to be maximized to achieve high charge carrier mobility.In all calculations,one PDI molecule is randomly chosen from the crystal structure as the middle molecule for a charge to diffuse and the nearest neighbor molecules in the crystals were taken to evaluate the transfer integrals.All possible intermolecular hopping pathways were generated.It is worth noting that only the nearest neighbor molecules in the crystals of 1-4 were taken to evaluate the transfer integrals and the direct dimer Hamiltonian evaluation method was used.The transfer integral for hole/electron transfer in the direct method can be written as[12-14]:

where Φ0,site10000000HOMO/LUMOand Φ0,site20000000HOMO/LUMOare the HOMO or LUMO of isolated molecules 1 and 2 of the dimer,respectively,and F0is the Fock operator for the dimer for a fixed pathway,in which the suffix of zero indicates that the molecular orbitals appearing in the operator(the density matrix,for instance)are unperturbed.The Fock matrix is evaluated as:

where S is the overlap matrix for the dimer,and the Kohn-Sham orbital C and eigenvalue ε are obtained by the zeroth-order Fock matrix without any self-consistent field iteration.

The diffusion coefficient can be evaluated from the hopping rates as[15]:

In the above equation,i represents a specific transfer pathway with ribeing the transfer distance(intermolecular center to center distance),Withe hopping rate due to charge carrier to the its neighbor,and n the spatial dimension,which is equal to 3 for the crystal.Piis the relative probability for its neighbor.The assumption is that the charge transfer is a slow process in which the molecules have enough time to become equilibrium.This is pertinent for the soft organic system.

Fig.1 Schematic molecular structures of compounds 1-4 The drift mobility(μ)of hopping is evaluated from the Einstein relaxation,

The molecular structures of the series of PDI compounds 1-4 are shown in Fig.1.The neutral molecules,cations,and anions of 1-4wereoptimizedatthesame set,that is,the hybrid density functional B3LYP(Becke-Lee-Young-Parr composite of exchangecorrelation functional)method and the 6-31G(d)basis set,which has been proved suitable for calculating large molecules in the previous work[7].Reorganization energies of 1-4 are provided by carrying out series of single point energy calculations on the basis of the optimized structures.Transfer integrals in all the possible dimers composed of two neighboring PDI molecules for 1-4 were studied according to the direct method[12-14].All the calculations were performed using the Gaussian 03 program[16]in the IBM P690 system at the Shandong Province High Performance Computing Center.

2 Results and discussion

2.1 Energy level of HOMO and LUMO and ionization energy and electron affinities

The calculated HOMO and LUMO energies together with the HOMO-LUMO gap for 1-4 are tabulated in Table 1.Introduction of chlorobenzyl or fluorobenzyl groups onto the PDI molecule leads to a little decrease in the HOMO and LUMO energies from -6.111 and-3.571 eV for 1 to-6.117--6.177 eV and-3.572--3.653 eV for 2-4,and a slight change in their HOMO-LUMO gap.Due to the n-type semiconductor property revealed for 1[17], compounds 2-4 should also be potential n-type semiconductor in terms of their frontier molecular energy levels.

The adiabatic and vertical ionization energies(IEaand IEv)and the adiabatic and vertical electron affinities(EAaand EAv)for the series of compounds 1-4 are calculated and the results are orga-nized in Table 2,which can provide more direct information for hole and electron injection from the Au source-drain electrode to the semiconductor layers than frontier molecular orbital energy. Accordingtopreviousresearches[18],semiconductormaterialswith the electronic affinity being in the range of 3.0-4.0 eV can ensure both efficient electron injection from common Au sourcedrain electrode and enough ambient stability and therefore show advantage as n-type semiconductors for OFETs.In line with the energy change of HOMO and LUMO,introduction of chlorobenzyl or fluorobenzyl groups leads to a high EAaof 2.543,2.495, and 2.578 eV for 2-4,respectively,which are larger than that of 2.395 eV for 1.The EAaof 2-4,2.50-2.58 eV,approaches the suggested electronic affinity for n-type semiconductor,suggesting the n-type nature of these three compounds.This is in line with the experimental result that N,N′-bis(4-trifluoromethybenzyl)perylene-3,4,9,10-tetracarboxylic diimide(PTCDI-TFB)exhibites n-type semiconducting properties[19].

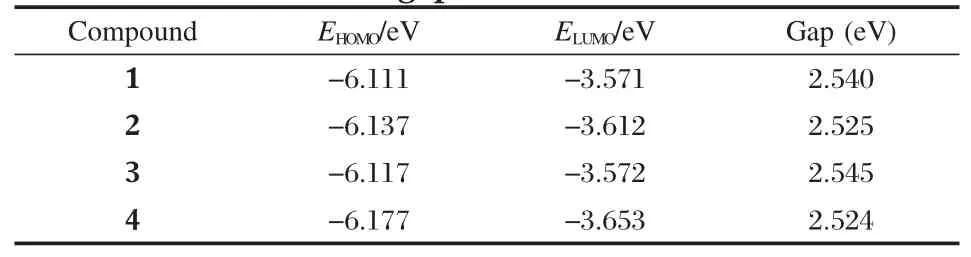
Table 1 Energies of frontier orbitals and HOMO-LUMO gaps of 1-4

2.2 Reorganized energy(λ±)

The calculated reorganization energies(λ±)for hole-transport and electron-transport process of the four compounds are listed in Table 3.The reorganization energy for electron(λ-)of 2-4, 0.3083,0.2920,and 0.2954 eV,respectively,is larger than that of 1,0.2450 eV,suggesting the smaller mobility of electrontransport for the three compounds than 1 in terms of reorganizationenergy(λ-).Thecomputedreorganizationenergyof1,0.2450 eV,corresponds well with the previous findings that reorganization energy for electron of PDI-C8,7is 0.25 eV using B3LYP functional with 6-311g(d,p)basis set[20].

Due to the strong coupling between the geometric and electronic structures,the small reorganization energy of these PDI compounds can be rationalized by the small geometric change of the neutral molecule when removing an electron from the HOMO or adding an electron into the LUMO[21].To further understand the change in the internal reorganization energy of these compounds,the geometry deformation of the neutral molecule upon reduction for 4 is studied(Fig.S2 and Table S1 (Supporting Information)).It is well known that the degree of geometry change for 4 upon reduction correlates to the orbital composition of LUMO.As can be seen from Fig.2,the LUMO of 4 mainly distributes over the carbon atoms of perylene core,the four oxygen atoms,and carbon atoms of diimide.The nitrogen,fluorin,hydrogen,and carbon atoms of benzene ring have no contribution to the LUMO of 4.As a consequence,one election reduction leads to structure change mainly in the C—C and C—O bond length for 1,with the largest bond length difference of 0.0834 and 0.119 nm.Upon reduction,the largest bond length modification for both C—C and C—O in 4 in compari-son with neutral molecule is 0.302 and 0.118 nm.As expected,variation in the C—H,C—N,and C—F bond lengths for 4,0.0101, 0.0615,and 0.0484 nm,respectively,is negligible.This is also true for 2 and 3.The larger geometric change for 4 upon reduction in comparison with 1 well rationalizes the larger reorganization energy for electron transfer process in 4 than in 1.

Table 2 Vertical and adiabatic ionization energies and electron affinities of 1-4

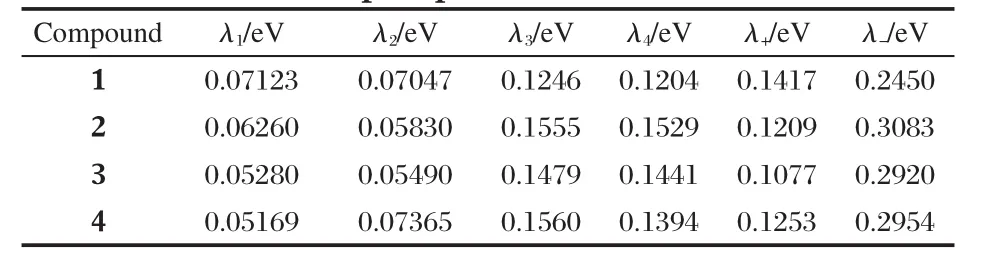
Table 3 Reorganization energies of hole-and electrontransport processes for 1-4

Fig.2 Molecular orbital maps of LUMO for compound 4

2.3 Intermolecular transfer integral(V)and charge transfer mobility(μ)in crystal

Compounds 1-4 all adopt herring-bone packing manner.The crystal structure and the hopping routes for 3(space group P21/a) are displayed in Fig.3 and Fig.4,respectively,as an example.All the possible transfer routes in the crystal of 1-4 are given in Table 4.Charge transfer integrals between one randomly selected PDI molecule(m0)(middle molecule in purple in Figs.(3,4)) and all its neighboring PDI molecules(m1-m15)are calculated on the basis of the experimental crystal structure of 3.According to the transfer distance,we divided the fifteen dimers between m0 and m1-m15 into six types.The nearest distance from m0 to m5,m8,m9,m11 is about 73 nm in type I.The second nearest distance is 120 nm from m0 to m6 and m7 in type II. As can be seen from Table 4,the farthest distance is 183 nm from m0 to m4 and m13 in type III.The center mass distance in the dimers composed of m0 and m2,m3,m10,m12 is 142 nm in type IV.Compared with type III,the second farthest distance is 180.3 nm from m0 to m1 and m15 in type V.According to the calculation,the distance between middle molecule and m14 is 138.5 nm and the intermolecular transfer integral is 0 meV in type VI.Among the six types of dimers,the largest transfer integral for electron is obtained for type I,about 19.1 meV,indicating the most favorable route for electron transfer in type I due to the largest overlapped stacking mode of molecules m5,m8,m9,and m11 relative to m0 in type I,Fig.5.As can be seen from Table 4,type V displays the second smallest transfer integral of only 0.012 meV for electron,indicating the most unfavorable route for electron transfer in type V due to the smallest overlapped stacking mode of molecules m1 and m15 relative to m0,Fig.6.

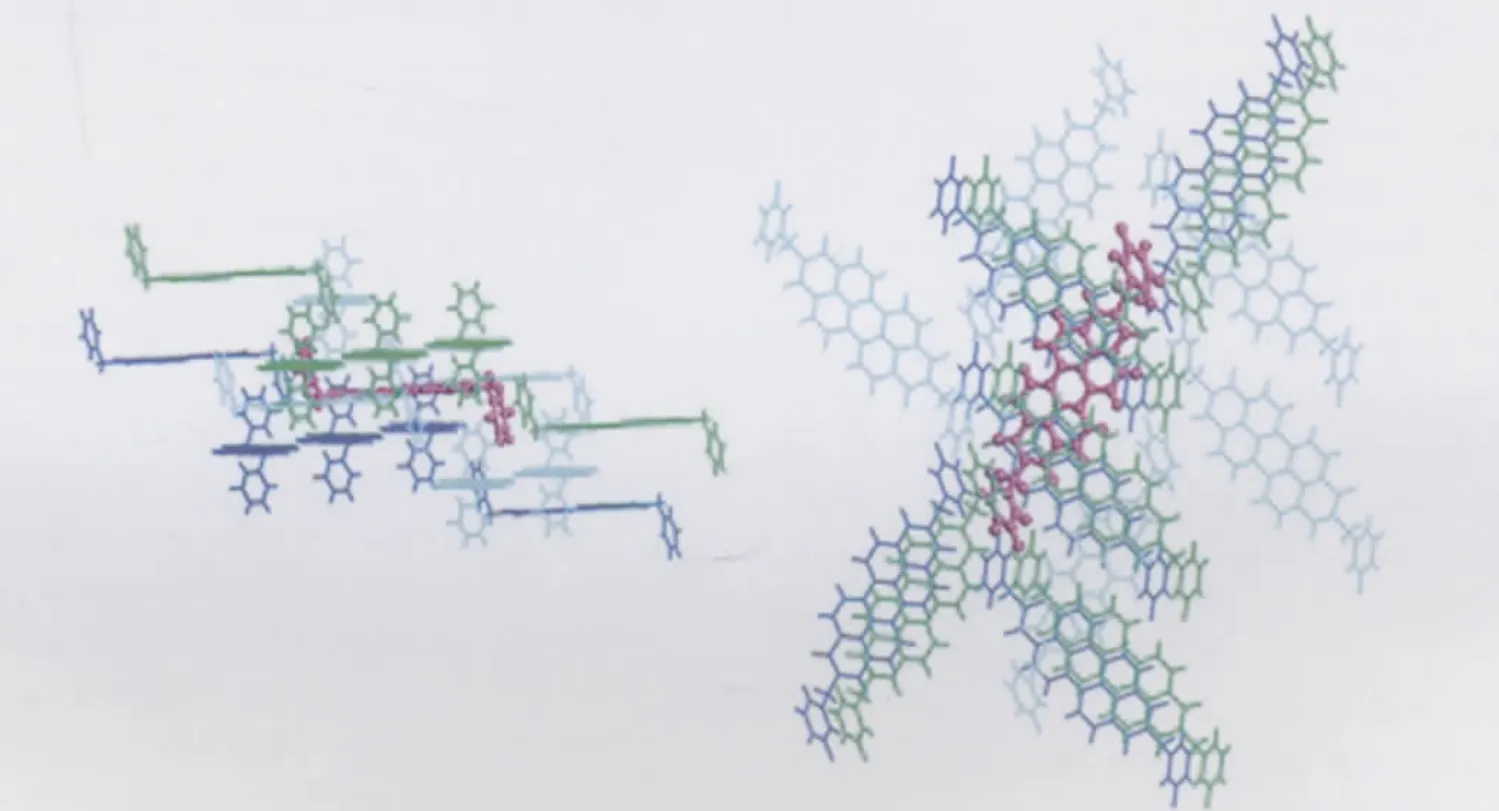
Fig.3 Crystal structure of 3(space group P21/a)in the crystalleft:side view;right:top view

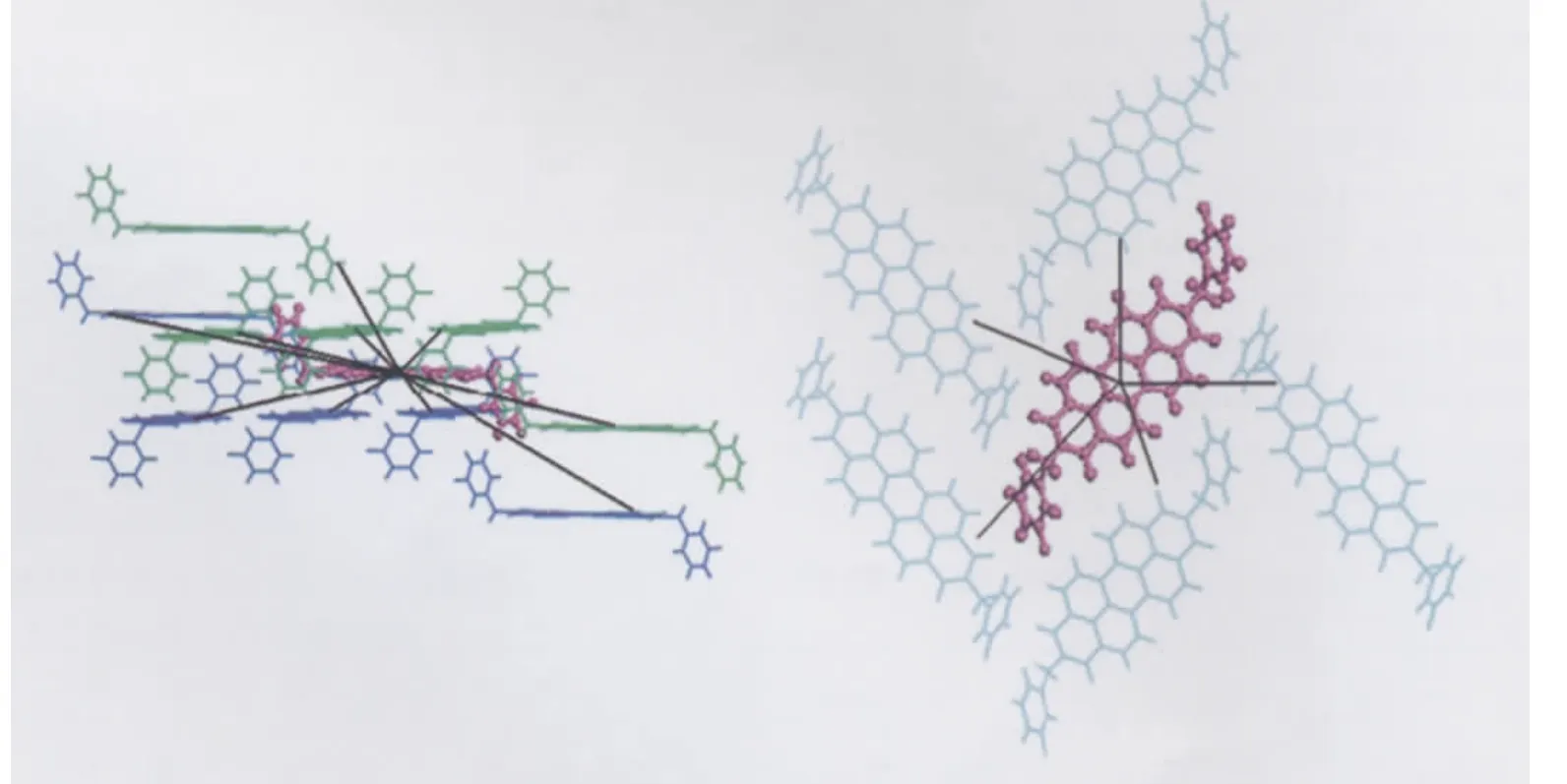
Fig.4 The hopping route of 3(space group P21/a)in the crystalleft:side view;right:top view

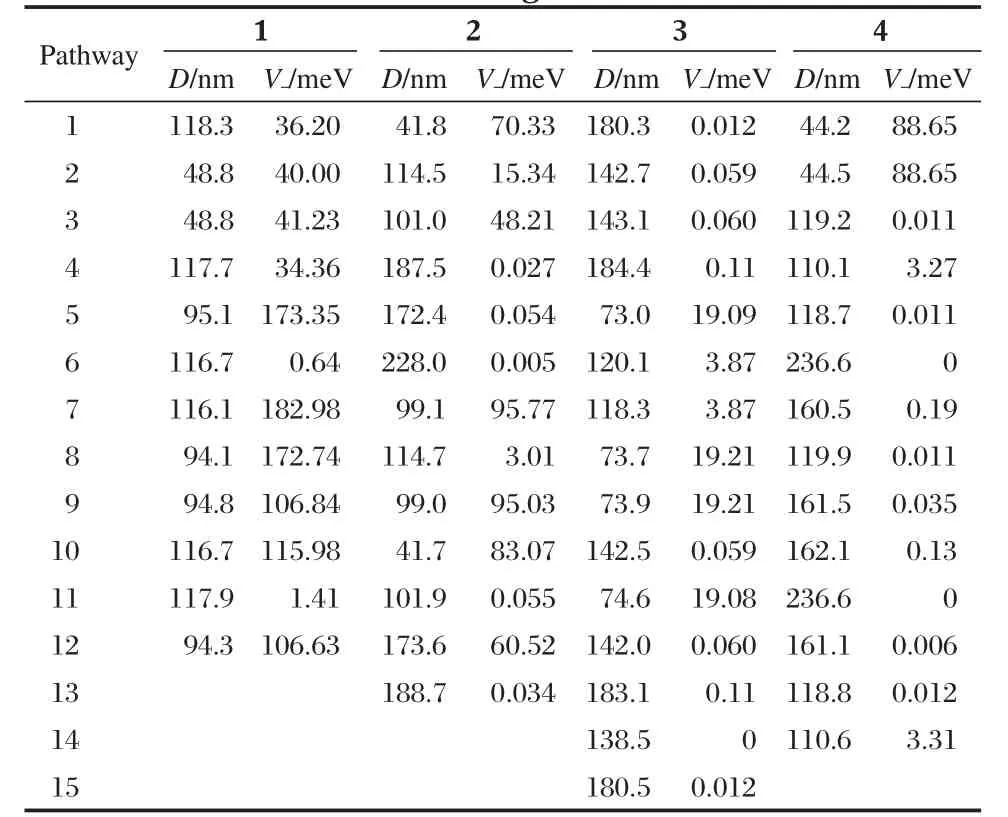
Table 4 The hopping pathways,center mass distance,and transfer integral of 1-4

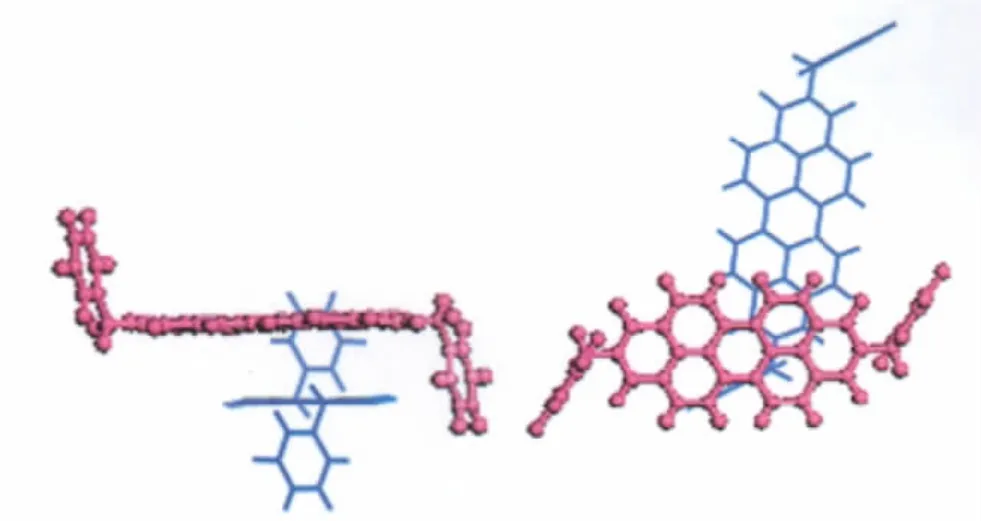
Fig.5 The hopping route of m0→m5 for 3 in the crystalleft:side view;right:top view

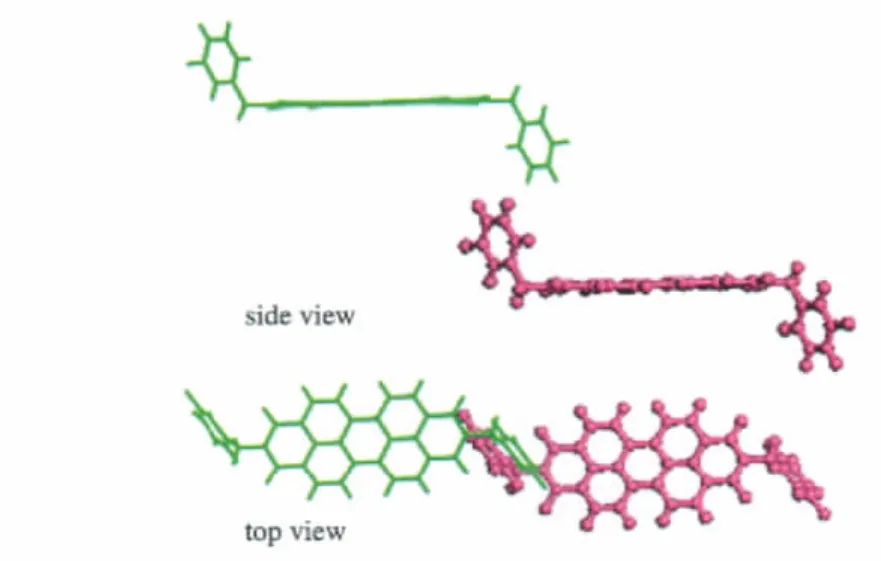
Fig.6 The hopping route of m0→m1 for 3 in the crystal

Table 5 Space group and mobility(μ-)of 1-4

The hopping pathways,center mass distance(D),intermolecular transfer integral(V),and mobility(μ)of 1-4 are also tabulated in Tables 4 and 5.As can be seen from Table 4,the largest transfer integral for electron among all the possible routes in the crystal of 1 is 182.98 meV,which is much larger than the largest transfer integral in the crystals of 2-4.These results indicate that the LUMO orbital coupling in the crystal of 1 is much stronger than that in the crystals of 2-4.

On the basis of the calculated transfer integral,intrinsic charge transfer mobility for electron in the crystals of 1-4 is calculated.The calculated intrinsic mobility in the crystal of 1-4 for electron is 5.39,0.59,0.023,and 0.17 cm2·V-1·s-1,respectively,indicating that the series of PDI compounds are good ntype semiconductors[22-25].The transfer mobility for electron in the crystal of 1 is much larger than those of 2-4,consistent with the trend for the largest transfer integral.Corresponding well with the experimental findings that the electron mobility of N,N′-bis (4-trifluoromethybenzyl)perylene-3,4,9,10-tetracarboxylic diimide (PTCDI-TFB),0.041 cm2·V-1·s-1,was obtained in air for the thin film[19],compounds 3 shows good n-type semiconductor property with the calculated intrinsic charge transfer mobility for electron of 0.023 cm2·V-1·s-1.

3 Conclusions

In summary,the charge transfer properties of a series of PDI derivatives for OFET applications were studied by density functional theory(DFT)calculations.Introduction of the chlorobenzyl or fluorobenzyl groups onto PDI is revealed to lower the HOMO and LUMO energy level and increase the electron affinity.The transfer integral and charge mobility values for the series of compounds with known crystal structure were also calculated.The calculation results reveal that the series of PDI derivatives are good n-type semiconducting materials with intrinsic mobility achieving 5.39,0.59,0.023 and 0.17 cm2·V-1·s-1for electron,respectively.And the charge transfer mobility for electron calculated for 3 corresponds well with the previous experimental findings.The present work will be helpful in developing novel PDI semiconducting materials for practical OFET applications.

Supporting Information Available: Illustration of the internal reorganization energies of charge self-exchange process, atom labels of 4,and B3LYP/6-31G(d)optimized geometries of neutral and anion of 4 have been included.This information is available free of charge via the internet at http://www.whxb.pku. edu.cn.

1 Dimitrakopoulos,C.D.;Malenfant,P.R.L.Adv.Mater.,2002, 14:99

2 Tsumura,A.;Koezuka,H.;Ando,T.Appl.Phys.Lett.,1986,49: 1210

3 Jones,B.A.;Antonio,F.;Wasielewski,M.R.;Marks,T.J.J.Am. Chem.Soc.,2007,129:15259

4 Ling,M.M.;Erk,P.;Gomez,M.;Bao,Z.N.Adv.Mater.,2007, 19:1123

5 Schmide,R.;Ling,M.M.;Hak,O.J.;Bao,Z.N.Adv.Mater., 2007,19:3692

6 Jones,B.A.;Ahrens,M.J.;Yoon,M.H.;Facchetti,A.;Marks,T. J.;Wasielewski,M.R.Angew.Chem.Int.Edit.,2004,43:6363

7 Kuo,M.Y.;Chen,H.Y.;Chao,I.Chem.-Eur.J.,2007,13:4750

8 Cai,X.;Zhang,Y.X.;Qi,D.D.;Jiang,J.Z.J.Phys.Chem.A, 2009,113:2500

9 Zhang,Y.X.;Cai,X.;Bian,Y.Z.;Li,X.Y.;Jiang,J.Z.J.Phys. Chem.C,2008,112:5148

10 Zhang,Y.X.;Cai,X.;Qi,D.D.;Bian,Y.Z.;Jiang,J.Z.J.Phys. Chem.C,2008,112:14579

11 Cai,X.;Zhang,Y.X.;Qi,D.D.;Jiang,J.Z.Sci.China Ser.BChem.,2009,39:393 [蔡 雪,张跃兴,齐冬冬,姜建壮.中国科学B辑:化学,2009,39:393]

12 Yang,X.D.;Wang,L.J.;Shuai,Z.G.Chem.Mater.,2008,20: 3205

13 Yin,S.;Yi,Y.;Li,Q.;Yu,G.;Liu,Y.;Shuai,Z.G.J.Phys.Chem. A,2006,110:7138

14 Wang,L.J.;Nan,G.J.;Yang,X.D.;Peng,Q.;Li,Q.K.;Shuai,Z. G.Chem.Soc.Rev.,2010,DOI:10.1039/b816406c

15 Yang,X.;Li,Q.;Shuai,Z.G.Nanotechnology,2007,18:4240299

16 Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03. Revision B.05.Pittsburgh,PA:Gaussian Inc.,2003

17 Chen,Z.J.;Debije,M.G.;Debaerdemaeker,T.;Osswald,P.; Würthner,F.ChemPhysChem,2004,5:137

18 Newman,C.R.;Frisbie,C.D.;da Silva,D.A.;Bredas,J.L.; Ewbank,P.C.;Mann,K.R.Chem.Mater.,2004,16:4436

19 Hosoi,Y.;Tsunami,D.;Ishii,H.;Furukawa,Y.Chemical Physics Letters,2007,436:139

20 Marcon,V.;Pisula,W.;Dahl,J.;Kirkpatrick,J.;Patwardhan,S.; Grozema,F.;Andrienko,D.J.Am.Chem.Soc.,2009,131:11426

21 Brédas,J.L.;Street,G.Acc.Chem.Res.,1985,18:309

22 Unni,K.N.N.;Pandey,A.K.;Alem,S.;Nunzi,J.M.Chemical Physics Letters,2006,421:554

23 Tatemichi,S.;Ichikawa,M.;Koyama,T.;Taniguchi,Y.Applied Physics Letters,2006,89:112108

24 Jung,T.;Yoo,B.;Wang,L.;Dodabalapur,A.Applied Physics Letters,2006,88:183102

25 Singh,T.B.;Erten,S.;Zafer,C.;Turkmen,G.;Kuban,B.;Teoman, Y.;Sariciftci,N.S.;Icli,S.Organic Electronics,2006,7:480