结合亚格子模型的Lattice－Boltzmann算法

罗 寅 张阿漫 朱永凯 徐珊珊

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001

结合亚格子模型的Lattice－Boltzmann算法

罗 寅 张阿漫 朱永凯 徐珊珊

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001

介绍一种亚格子模型与LB（Lattic－Boltzmann）方法相结合的算法，并用其对亚临界雷诺数情况下的圆柱绕流问题进行数值模拟，得到流场的流线图以及圆柱表面的压力系数。通过与实验值相比较，发现数值结果与实验值是比较吻合的，证明该算法可以用于计算雷诺数较大的流体问题，同时具有LB方法计算效率高的优点。

格子Boltzmann方法；亚临界雷诺数；圆柱绕流

1 引言

近年来，备受人们关注的LB方法通过利用粒子的简单且规则统一的假想运动模型来代替复杂的真实微观运动，从而达到实现模拟宏观物理现象的目的。LB方法的前身是格子气自动机（Lattice Gas Automata，LGA［1］）。 LB 方法使用中观的实数型变量—粒子分布函数替代了LGA的微观的布尔型变量，从而不再需要具体计算微观量，而是直接按Lattic－Boltzmann方程来模拟宏观现象。LB方法应用最广泛的模型是单松弛模型［2］，它与分子动理论中Boltzmann方程的BGK（Bhatnagar－Gross－Krook）算子类似，故这类模型又称为“LBGK 模型”［3］。LB 方法与传统的 CFD 方法相比，在问题的求解规模和求解速度方面，有着后者无法比拟的优势。在水力学问题、多相流、对流扩散问题及求解偏微分方程等许多方面，LB方法都展示了广阔的应用前景，甚至传统的CFD方法难以模拟的多孔介质问题，LB方法也能从容处理。LB方法还能够模拟一些没有宏观控制议程的问题。但是，和传统方法相比，LB方法也有不足的地方，表现在所能求解的实际问题雷诺数范围太低，一般只有低于103时，才有满意的精度，而当雷诺数进一步提高时，计算容易失稳。本文将传统的亚格子模型成功地运用到LB方法中，显著地提高了LB方法的适用范围。

2 LB方法简介

在 LB 方法中，粒子分布函数 fα（x，t）的演化方程可写成如下形式：

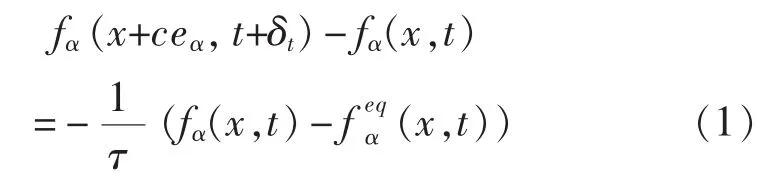
式中，fα（x，t） 为沿 α 方向的粒子分布函数；c＝Δx／Δt，Δx、Δt分别为空间和时间步长， 可取Δx＝Δt，即 c＝1。

LB方法应用较多的是二维九点模型（D2Q9）。

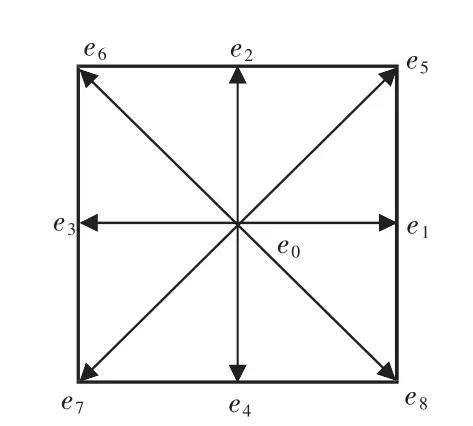
图1 D2Q9模型速度张量图

这里，α ＝0，…，b（b ＝8）；eα为粒子的运动方向；τ为驰誉时间；f（x，t）为沿 α 方向的粒子平衡分布函数。

将演化方程（1）按照 Chapman－Enskog展开，并进行尺度粘合［4］可以得到流场控制方程，即连续性方程和N－S方程。在节点上的宏观量（密度、速度和压力）与粒子分布函数满足方程：

D2Q9模型的驰誉时间与粘性系数满足下面的关系：

3 格子Boltzmann亚格子模型

从数值计算角度看，LB方法可以看作是求解N－S方程的一种数值方法，同传统的流体力学方法一样，要直接计算雷诺数较高流体问题就意味需要降低网格尺度，这样对计算机的硬件要求是很高的，相应的计算时间也成倍增长，并且在LB方法中对马赫数是有要求的，因此，流场速度也是受限制的。传统的方法在求解湍流问题时将其分为两种尺度，大尺度运动由N－S方程描述，小尺度运动的耗散作用及其对大尺度运动的反馈，则通过引入湍流模型来描述。亚格子模型便是其中一种。亚格子模型沿袭了湍流模式化方法，其中最早最常用的是气象学家 Smagorinsky［5，6］在 1963 年提出的涡粘性模型。该模型假定用各向同性滤波器滤掉的小尺度脉动是局部平衡的，假定涡粘性正比于亚格子尺度的特征长度和特征湍流速度，以此求出亚格子应力。根据Smagorinsky提出的涡粘性模型可知：

为了将亚格子模型引入LB方法，假设粒子的碰撞过程仅与局部的粒子信息相关，保持模型中的平衡分布函数形式不变，其中的宏观物理量均用过滤后的平均量替代。D2Q9模型中弛豫时间与粘性的关系变为：

式中，粘性系νtotal分为物理动力粘性ν0和涡粘性νt两个部分。将亚格子模型涡粘性系数应用到式（6）中可以得到：

本文中滤波尺度Δ＝δx。根据节点的分布函数可以很容易的确定应变率张量Sij：

结合了亚格子模型的D2Q9模型演化方程最终形式为：

公式（9）与公式（1）有相同的形式，不同之处在于原模型中弛豫时间是固定值，本文通过引入亚格子模型对弛豫时间进行了修正。在计算过程中，弛豫时间根据每步计算结果的变化而变化。这个特点说明，使用本文所引入的方法同使用原LB方法具有相同的计算流程，只是在每一个迭代时间步开始前，利用公式（7）完成对弛豫时间的修正即可。

4 圆柱绕流算例

为了证明本文方法的有效性，本文使用D2Q9模型，对亚雷诺数条件Re＝1.6×104圆柱绕流进行数值模拟 流场区域结构如图2所示

众所周知，对圆柱绕流问题而言，当雷诺数超过一定数值时，在圆柱后面会产生周期性的旋涡，俗称“卡门涡街”。图3所示为计算结果稳定后，截取圆柱附近的流场向量图。图4是对应的流线图，截取间隔时间为2 s。由该图可以明显地看到，在圆柱后面出现了旋涡，并且旋涡在柱体左右两侧交替地产生、发放。圆柱绕流的这种旋涡发放是周期性的。

随着涡街的周期性发放， 在柱体表面会受到周期性的升力FL和阻力FD。在圆柱绕流计算中，参数Strouhal（简称St）数是表明旋涡脱落特性的相似准则数，是升力频率fs的无因次表达。在本文算例中，经过计算得到St的值为0.21。而根据实验研究得到，在亚临界雷诺数区范围时，即30≤Re＜3 ×105时，St约等于 0.2， 两者相对误差是5%。流体流过圆柱的时候，圆柱会受到升力和阻力是因为在圆柱表面受对压力的结果。图6是圆柱表面无量纲稳态压力系数Cp计算值与实验值对比图。

图5 圆柱表面的Cp 值变化图

从图5可以看出，Cp的计算值与实验值是非常吻合的。另外，由于随时间变化的涡激励是一个平稳随机过程，因此通常采用无因次脉动阻力系数 CD′，脉动升力系数 CL′来表达脉动阻力值、脉动升力值。 本文中 CL′＝ 0.55，CD′＝ 0.1，这是符合实验值［6］的。

5 结论

本文将传统的亚格子模型应用于LB方法，用该算法模拟了亚临界雷诺数条件下的圆柱绕流问题，并通过将数值模拟的结果与实验值对比，证明了这种方法的有效性。

［1］FRISCH U，HASSIACHER B，POMEAU Y.Lattice gas automata for the Navier－Stokes equation［J］.Physical Review Letters， 1986，56（14）：1505－1508.

［2］QIAN Y H，HUMIERES D，LALLEMAND P.Lattice BGK models for the Navier－Stokes Equation［J］.Europhys.Lett，1992，（6）：479－484.

［3］GUO Z L，SHI B C，WANG N C.Lattice BGK model for incompressible Navier－Stokes equation ［J］.J Stat Phys，2000（165）：288－306.

［4］SUCCI S， HUMIRES D D＇， QIAN Y H， el at.On the small－scale dynamical behavior of lattice BGK and lattice Bolzmann schemes ［J］.J.Sci.Computing，1993，8 （3）：219－230.

［5］SMAGORINSKY J.General circulation experiments with primitive equations［J］.Mon Weather Rev，1963（91）：99－165.

［6］SMAGORINSKY J.General circulation experiments with the primitive equations part I：the basic experiment［J］.Mon.Weather Rev.，1963， 91（1）：99－165.

Combination of the Lattice-Boltzmann Method and the Sub-grid Model

Luo Yin Zhang A－man Zhu Yong－kaiXu Shan－shan

College of Shipbuilding Engineering， Harbin Engineering University， Harbin 150001，China

An algorithm to combine the Lattice－Boltzmann （LB） method and the sub-grid model is introduced and is used to simulate the flow around a cylinder under subcritical Reynolds number.The obtained streamline of the flow field and the pressure coefficient around the cylinder are found to agree well with the data from tests.The agreement indicates that the discussed method suits those problems with relatively high Reynolds number and inherits the computation efficiency of the LB method.

Lattice Boltzmann method； subcritical Raynolds number； flow around cylinder

U661.73

A

1673－3185（2010）01－10－04

2009 - 06 - 26

罗寅（1985 － ） ，男，硕士研究生。研究方向：船舶与海洋结构物性能与安全性。E-mail：luoyinlsq@ 163. com

张阿漫（1981 - ） ，男，副教授。研究方向：船舶与海洋工程结构动力学