大侧斜螺旋桨强度校核探讨

黄 毅 许 辉 姜治芳

1大连船舶重工集团有限责任公司军事代表室，辽宁大连 116005

2中国舰船研究设计中心，湖北 武 汉 430064

大侧斜螺旋桨强度校核探讨

黄 毅1许 辉2姜治芳2

1大连船舶重工集团有限责任公司军事代表室，辽宁大连 116005

2中国舰船研究设计中心，湖北 武 汉 430064

针对大侧斜螺旋桨复杂的几何外形和载荷分布，为准确解决其强度校核问题，介绍了两种螺旋桨强度校核方法，传统的悬臂梁法和有限元法。前者视桨叶为变截面的悬臂梁，按正车最大航速时的静态负荷来进行校核；采用有限元法在全速正车和紧急倒车状态时计算叶片的应力应变，重点介绍了紧急倒车过程中作用在桨叶上最大水动力载荷的确定方法。最后通过算例分析，比较两种方法校核同一螺旋桨强度的结果，指出有限元法更适合用于大侧斜螺旋桨的强度校核。

大侧斜螺旋桨；强度校核；悬臂梁法；有限元法

1 引言

螺旋桨的叶片侧斜增大能够使作用在船后不均匀来流中的不定常力减小，同时降低由于螺旋桨旋转引起的船体振动，减小推进器噪声，因此大侧斜螺旋桨在船舶领域得到了广泛的应用，对其强度的校核是设计中必须解决的问题之一。

通常对螺旋桨的强度校核按照规范中要求的悬臂梁法来进行。但考虑到定距桨从全速正航到完全停止的倒车时，螺旋桨旋转方向改变，而此时船仍向前运动，在这种情况下，螺旋桨叶片的绕流是非定常不稳定的脱体绕流，导致水动力载荷急剧增长。尤其对于大侧斜螺旋桨而言，由于作用于各叶剖面中心水动力力臂比无侧斜桨大，倒车反转时引起的桨叶内应力比相同条件下无侧斜桨桨叶内应力大得多，因此这种状态特别危险，可能产生卷边甚至叶片梢部切面的破损。由于桨模倒车时的最大应力测量实施起来比较困难，非常耗时费力，属于一系列超出水池模型常规试验范围的复杂水动力试验，目前主要采用有限元法来解决。

2 悬臂梁法

悬臂梁法中视桨叶为变截面的悬臂梁，按正车最大航速时的静态负荷来进行校核，一般要求桨叶校核截面的强度储备系数K满足以下条件：

式中，σb为材料抗拉强度；σ为计算截面处最大计算应力；K1为规范要求强度储备系数衡准值。

桨叶剖面的正应力由推力、旋转阻力及离心力产生的弯曲和拉压引起，悬臂梁强度校核法可以按照以下步骤来进行［1］。

1）推力产生的弯矩计算

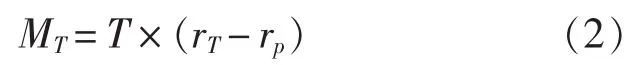
式中，T为正车最大航速工况下单片桨叶产生的推力；rT为正车最大航速工况下桨叶水动力作用中心的径向半径；rp为校核剖面的径向半径。

2）旋转阻力产生的弯矩计算

式中，PD为正车最大航速工况下单只螺旋桨的收到功率；Z为螺旋桨叶数；n为正车最大航速工况下螺旋桨转速。

3）离心力产生的弯矩计算

建立与螺旋桨相连的右手直角坐标系，如图1所示。坐标原点O为桨叶辐射参考线与轴线交点，Y轴表示航向，Z轴取向使零号叶片轴线位于YZ平面内。

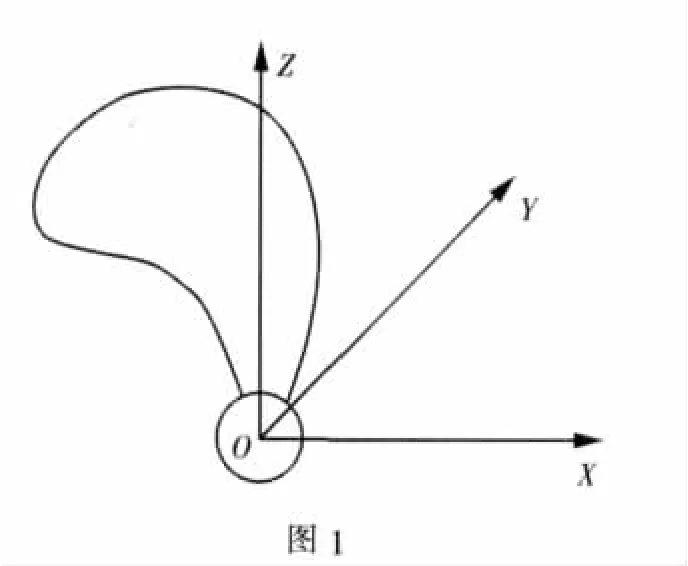
将各半径 r处叶剖面面积记为 S（r），Xc、Yc为各半径处叶剖面形心的坐标。则离心力为：

由于离心力位于Y＝YG平面内，与X轴正向夹角γ＝arccos（），因此离心力可以分解为沿X轴和Z轴的分量：

式中，XG、YG、ZG为校核剖面外桨叶质心 G的坐标。

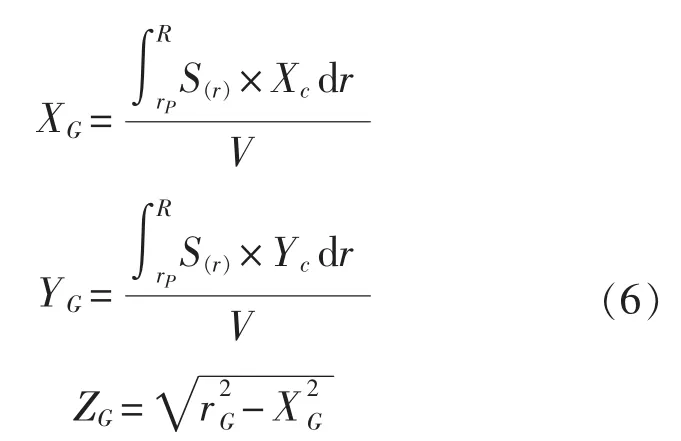
将所校核剖面形心记为C，将坐标系XOY平移至X′CY′，如图2所示。则离心力分量F离X对Y′轴产生的弯矩：

离心力分量F离Z对X′轴产生的弯矩：

离心力分量F离Z对Y′轴产生的弯矩：

式中，lg、ls为离心力分量 F离Z对 X′轴、Y′轴力臂。

4）合成力矩及剖面应力计算

将推力、旋转阻力及离心力产生的弯矩分解到校核切面的主惯性轴ξ—ξ轴和η—η轴上，如图2所示，则可得：

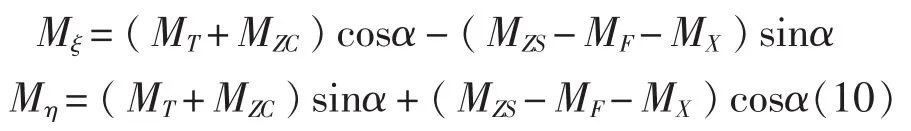
式中，α为所校核剖面处的螺距角。

将校核剖面上具有最大坐标ηmax或ξmax的点记为 A、B、C、D，如图 3 所示，计算弯矩 Mξ、Mη及F离Z在这些点上产生的总应力，从而得到校核剖面上的 σmax。

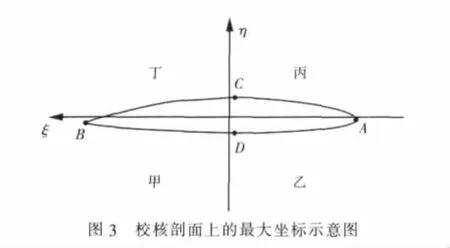
5）强度储备系数计算

3 有限元法

采用有限元法校核螺旋桨强度主要是在全速正车状态及紧急倒车状态时对确定的外载荷作用下叶片的应力应变状态进行计算［2－4］，再将正车及倒车状态下的安全系数与额定值进行比较。

由于船在倒车过程中水动力最大的状态下螺旋桨叶片的绕流极不稳定，导致叶片载荷呈现复杂的脉动现象，应用螺旋桨环流理论的分析方法来研究这些非定常、不稳定工作状态下螺旋桨水动力作用，效果很差，因此采用有限元法校核桨强度的关键在于确定倒车时作用在叶片上的外载荷。本文中简要介绍一种近似计算法，利用它可以得到倒车过程中桨叶经受的最大水动力载荷。

3.1 倒车计算状态的确定

从全速正车直至全部停止的紧急制动过程中，螺旋桨叶片工况变化可分为三个阶段。在第一阶段，从主机输出功率减小开始到螺旋桨的推力变为零的瞬间，螺旋桨转入水轮机工况，此阶段的持续时间由主机输出功率减小的速率决定；第二阶段，主机开始产生一个扭矩来平衡螺旋桨上的水动力矩，螺旋桨旋转变慢并停转；第三阶段螺旋桨产生负推力，在其作用下船体停止运动。

为了求出在所考虑的制动各阶段过程中流向螺旋桨的速度值及方向，必须对完成主机紧急倒车的船体运动进行计算。描述制动工况下船体平移运动及螺旋桨旋转的微分方程组如下：

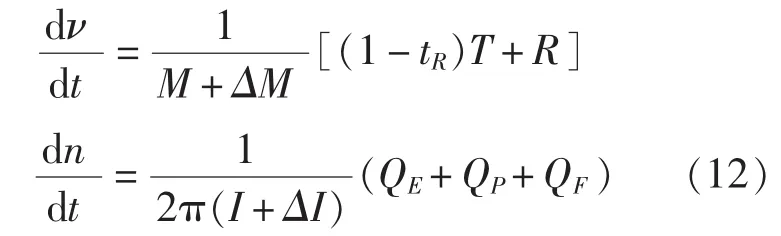
式中，ν为船体平移速度；n为螺旋桨转速；t为时间；M＋ΔM为考虑附连水质量的舰船质量；I＋ΔI为考虑附连水惯性矩的螺旋桨、轴系、减速器及主机的旋转质量的总惯性矩。

上述微分方程组相对于 ν（t）和 n（t）的关系式求解，按照Lunge－Kutta法进行。且还需要给出以下输入条件：

1）决定制动工况强度的主机转矩的时间关系 QE＝ f（t）；

2）螺旋桨准倒车水动力特性，反映螺旋桨推力系数Ktp及放大10倍的广义螺旋桨扭矩系数Kqp对角度β（以度计）的关系；

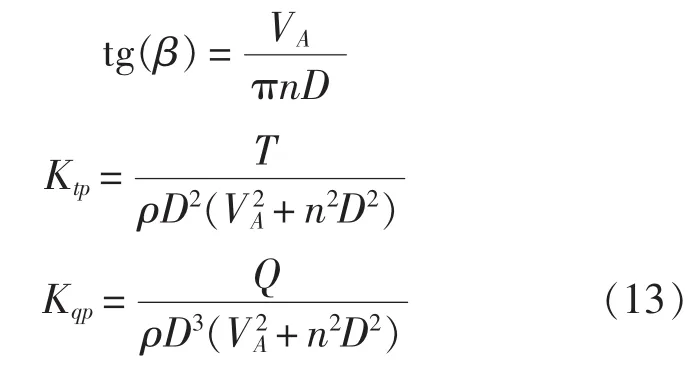
3） 阻力曲线 R（ν）；

4）伴流分数及推力减额。

求解过程中，在每一个瞬间根据已知的船速和螺旋桨转速来确定在相对半径0.7处的叶片绕流合速度 ω0.7，并假定从倒车开始后 ω0.7为最大值的瞬间对应螺旋桨经受最大的水动力载荷时刻。大量倒车计算表明，通常此瞬间船体继续向前运动，而螺旋桨转速达到倒车的最大值，处于制动过程的第三阶段。

3.2 叶片分离绕流载荷的确定

制动的第三阶段，船体在向前运动，而螺旋桨因反向旋转产生负推力并沿与螺旋桨的来流相反方向喷出水流。模型及实船倒车工况均表明，船体处于倒车状态时，螺旋桨的来流是不稳定的，会裂变成大尺度漩涡结构，无法利用准定常试验结果来确定作用在桨叶片上的水动力载荷，因此假设不考虑螺旋桨叶片间的水动力相互作用且叶片柱状切面的绕流等价于具有相同厚度的平板脱体绕流，估算作用于叶片上的最大载荷，则求得的值可能偏大，从而使最终结果偏安全。

利用计算平板脱体绕流时法向力的Pelea公式估算螺旋桨叶片切面上的作用力：

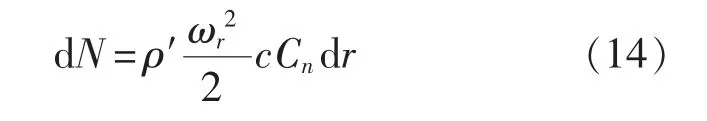
压力中心的坐标由以下公式得到：

通常情况下，压力中心在叶根部切面处从切面中心移近叶片导边，而在叶梢部切面处从切面中心移近随边 （按照正航状态下定义随边及导边）。因此：

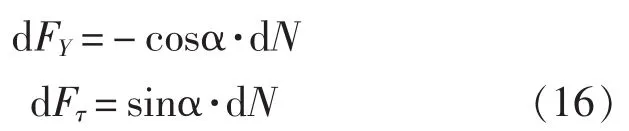
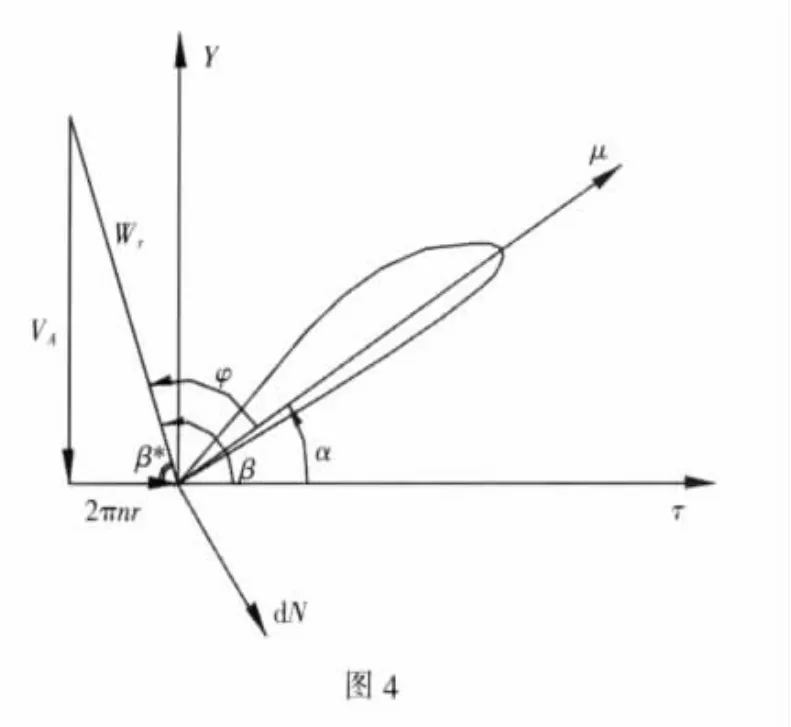
在图1的坐标系｛X，Y，Z｝中作用在叶片柱状切面上的水动力及离心力投影为：

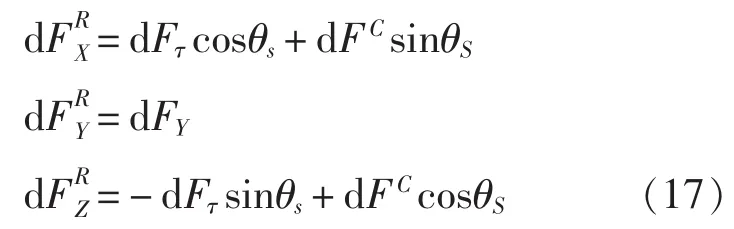
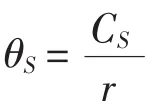
为了计算沿叶片柱状切面的载荷分布，需要求解联系平板上速度与沿切面弦长流动坐标的微分方程：

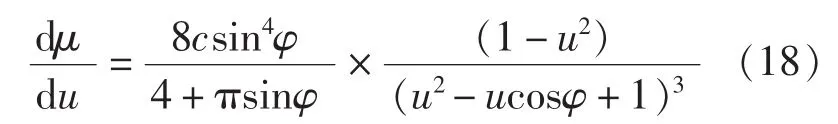
式中，μ为沿切面弦长的坐标；u为沿切面弦长的速度分布u（μ），且为以ωr为特征速度的无量纲值。同时u及压力由以下关系式联系：

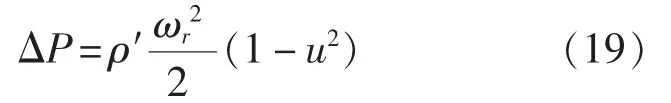
从而可以得到沿切面弦长的载荷分布ΔP（μ）。

4 算例分析

以某大侧斜螺旋桨为例，根据正车最大航速下的静态负荷，采用悬臂梁法计算0.3R叶剖面的最大应力并得到强度储备系数K＝0.75K1，按照规范中悬臂梁法校核，该桨叶不满足强度要求。

采用有限元法［5-6］对同一螺旋桨进行紧急倒车状态及正车最大航速状态下的强度校核计算，其中正车最大航速状态下螺旋桨的水动力载荷由升力面理论得到，倒车状态的外载荷由上述方式得到，计算这两种状态下桨叶压力面及吸力面的应力分布，如图5～图8所示。由图可见，叶片的应力分布与常规桨不同，最大应力区从叶片根部移向外缘切面，并从最大厚度线移向叶片随边。如紧急倒车工况下压力面的高应力区位于叶片0.5R～0.75R弦中部偏随边处，吸力面的高应力区位于叶片0.6R～0.75R弦中部偏随边处；且倒车时的最大应力约为正车工况时的1.5倍；从各应力分布图中还可发现，靠近叶梢部应力增加幅度更为明显。将计算的安全系数与强度储备系数额定值进行比较，得到螺旋桨强度满足要求的结论。

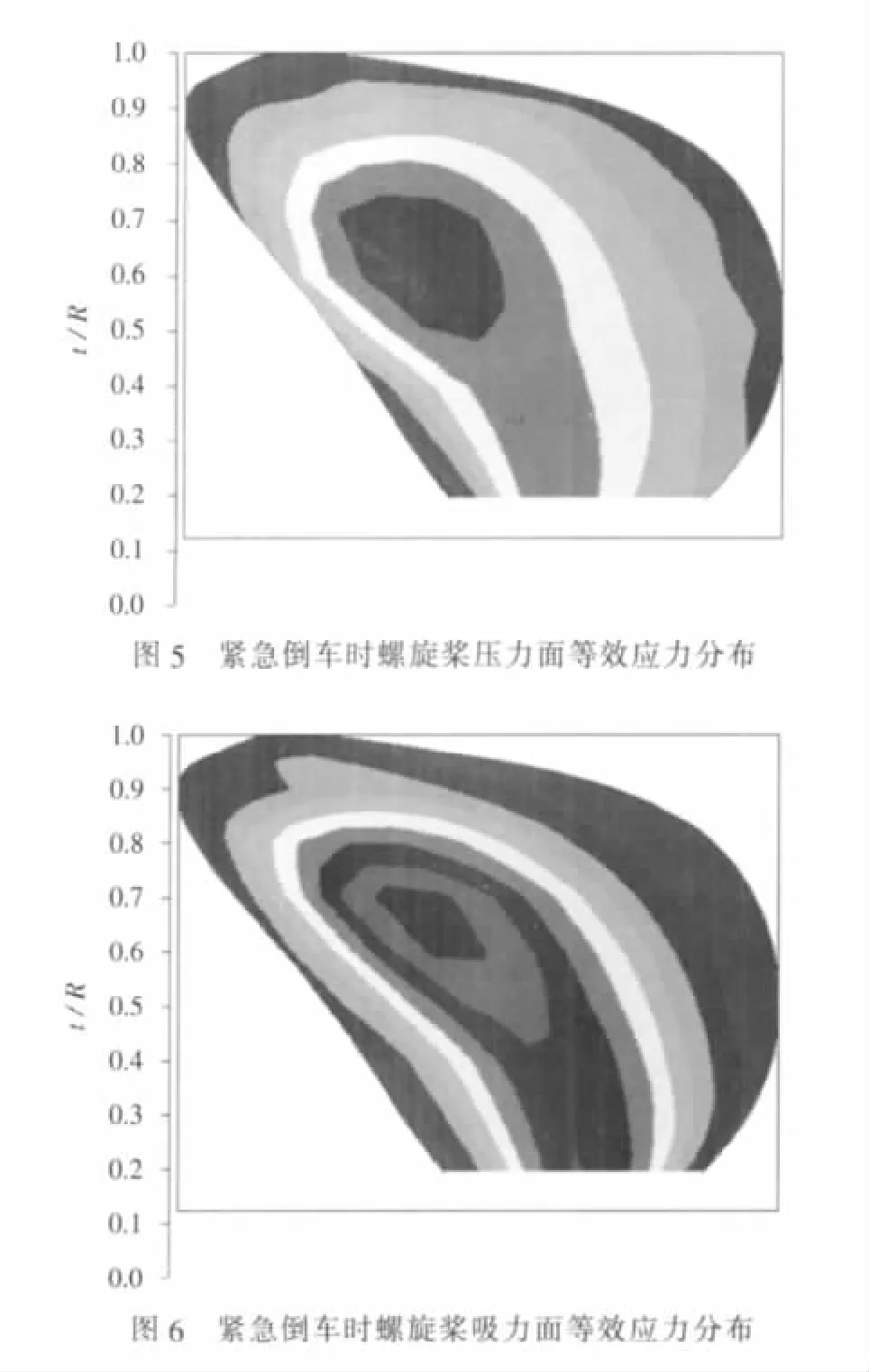
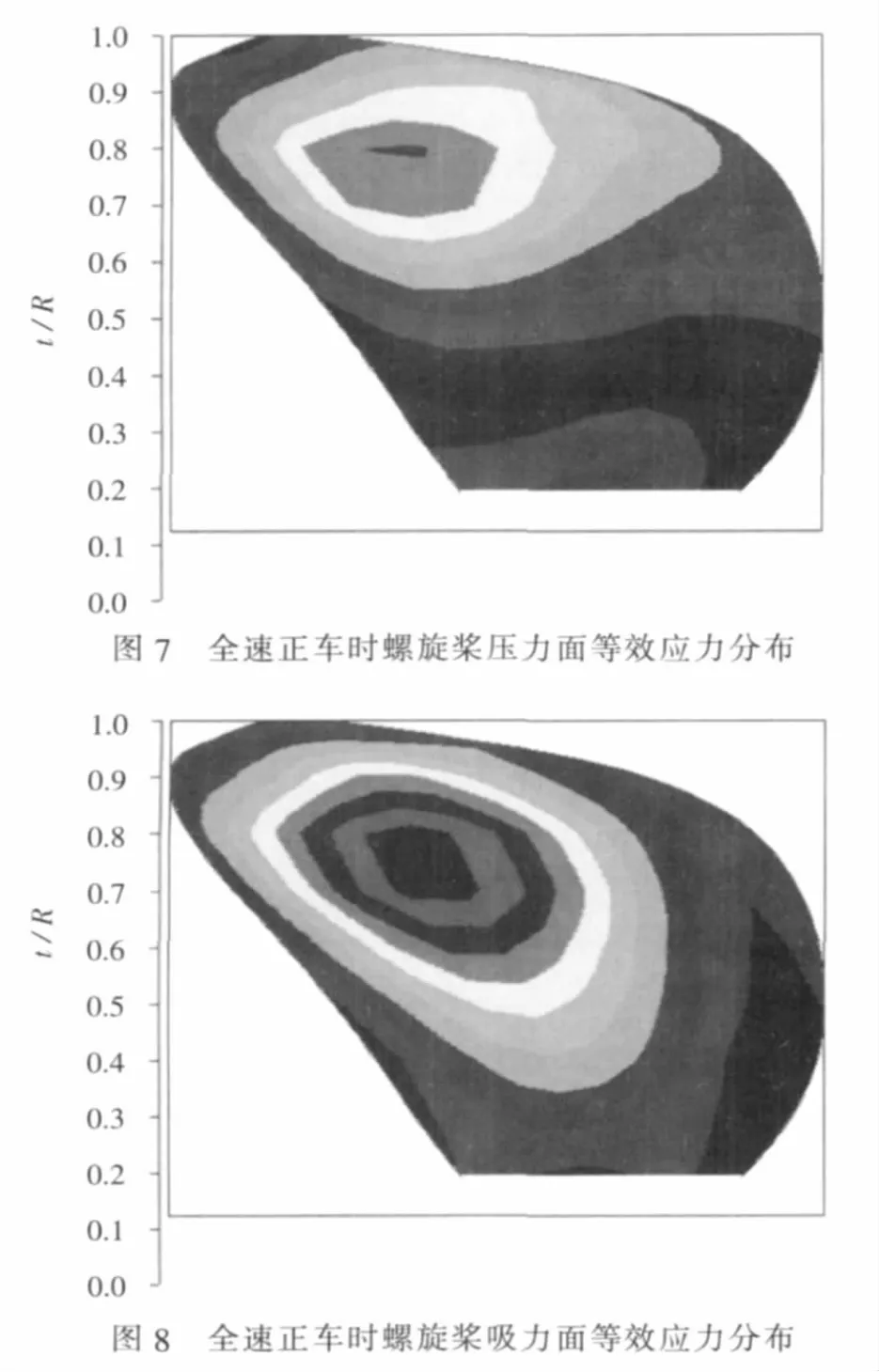
很明显，两种方法校核同一螺旋桨的强度得到不同结论。悬臂梁法虽然校核的是正车最大航速时静态载荷下的强度，但可以认为将紧急倒车工况下的最大应力储备到了系数K之中。对于大侧斜螺旋桨而言，由于其几何原因导致靠近叶根处剖面的最大应力比常规桨要大，此时若仍按照悬臂梁法来计算，其强度储备系数K≥K1将难以满足，而算例中的螺旋桨经过实船检验证明其强度符合要求，因此悬臂梁法中可能存在储备过大，过于保守的问题，将不再适合大侧斜桨的强度校核计算。采用有限元法对桨叶强度进行计算，可以直接得到全速正车和紧急倒车工况下桨叶最大应力的部位及大小，是更为准确的一种方法，日本学者进行的广泛的研究就证明了这一点［7］。

在大侧斜螺旋桨模型倒车破坏性试验中，破坏的桨叶断口指向0.6R的随边至0.9R的导边连线，也进一步验证了有限元法计算的准确性［8］。

5 结束语

大侧斜桨的几何外形及载荷分布都特别复杂，正、倒车工况下桨叶上的应力分布情况不同于常规桨，叶片的应力也比常规桨要大，在使用中极易发生倒车强度不足的问题，因此需要对其紧急倒车工况下的强度进行准确计算。而传统的悬臂梁法基于最大航速时的准静态载荷来校核强度，将不再适用于大侧斜桨，采用有限元法则是解决其倒车强度分析问题的有效途径。

［1］王国强，盛振邦.船舶推进［M］.北京：国防工业出版社，1985.

［2］王玉华.大侧斜螺旋桨强度研究［J］.船舶力学，1998，2（2）：44-51.

［3］索志强.船舶螺旋桨振动和强度的水弹性分析 ［D］.武汉：海军工程大学，1990.

［4］岳亚霖.大侧斜螺旋桨应力分析［D］.无锡：中国船舶科学研究中心，1990.

［5］万正权.螺旋桨桨叶强度有限元分析［R］.无锡：中国船舶科学研究中心，1988.

［6］王玉华.大侧斜螺旋桨专用强度有限元分析程序理论文本［R］.无锡：中国船舶科学研究中心，1993.

［7］YAMASAKI S.Highly Skewed Propeller ［R］.Jur Soc Nav Archit，Jap，Vol.153，1983.

［8］高同兵，程尔升.大侧斜螺旋桨设计中的考虑［J］.船海工程，2004（2）：1-3.

Strength Analysis of Highly－Skewed Propeller

Huang Yi1Xu Hui2Jiang Zhi-fang2
1 Military Representative Office in Dalian Shipbuilding Industry Co.Ltd.，Dalian 116005，China
2 China Ship Development and Design Center，Wuhan 430064，China

Considering complicated geometrical shape and load distribution of highly－skewed propeller，traditional cantilever beam method and Finite Element Method （FEM）are introduced to analyze the strength of propeller.The former method regards the propeller blades as beam with variable sections and is used to check the structural strength with static loading at the highest advanced speed.The lattermethod computes the stress and tension of blade at full speed forward and crash astern.Emphasis is placed on identifying effective approach to determine the highest hydrodynamic load on the blade when in crash astern operation.Both methods are utilized to compute the structural strength of highly－skewed propeller，the results show that FEM is more applicable than the traditional cantilever beam method for such structural strength analysis.

highly－skewed propeller； strength analysis； cantilever beam method； Finite Element Method

U664.33

A

1673－3185（2010）05－44－05

10.3969/j.issn.1673-3185.2010.05.009

2009－10-13

黄 毅（1978－），男，本科，工程师。研究方向：船舶设计。E-mail：hhmy78@126.com