基于奇异值分解的核磁共振测井T2 谱反演方法的改进
2010-02-27李鹏举孙国平王彦凯
李鹏举,葛 成,孙国平,陈 新,王彦凯
(1.大庆石油学院地球科学学院,黑龙江大庆163318;2.大庆钻探工程公司测井二分公司,吉林松原138000;3.大庆油田勘探开发研究院,黑龙江大庆163712)
0 引 言
核磁共振(NMR)测井弛豫信号的多指数在NMR岩心分析与测井解释反演结果的好坏直接影响到后续计算储层物性参数(如孔隙度、渗透率、孔径分布等)和T2截止值的准确性[1]。Butler等[2]、Dunn等[3]、王忠东和肖立志[4]先后讨论了罚函数法(BRD)、奇异值分解算法(SVD)以及联合迭代重建算法(SIRT)。Borgia等在罚函数法的基础上讨论了均匀惩罚的反演方法。Jonathan等用线性正则化的方法分析了由短弛豫组分构成的多指数弛豫数据的拟合问题,这些算法从不同的正则化角度给出了多指数反演的设计思路。此外,Mohnke等[5]利用模拟退火法优化反演中的随机搜索问题;Dunn等[6]讨论了对不同测量误差的原始回波数据进行组合反演的方法。本文基于矩阵分析理论,进一步改进奇异值分解反演方法。
1 核磁共振测井T2谱解谱方法
1.1 建立储层流体核磁共振模型
求解弛豫过程的Bloch方程可知,氢原子核系统磁化强度矢量的横向分量是按指数规律衰减的,由CPMG脉冲序列测得的回波串也按指数规律衰减。储层岩石通常存在1个孔隙尺寸分布,并且常常含有多种流体成分,此时孔隙中存在多种弛豫组分,即横向弛豫时间常数(T2)不是单值,而是1个T2谱分布。因此,由CPMG脉冲序列测量记录的自旋回波串按多指数规律衰减,即各单指数衰减的叠加
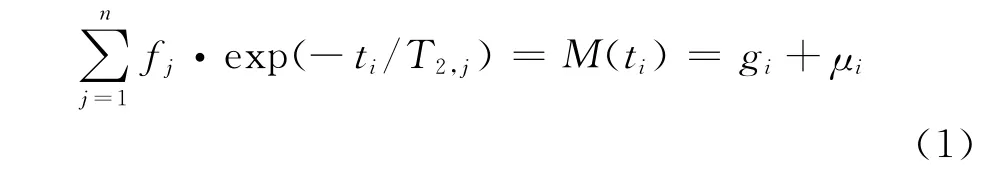
式中,m、n分别为测量到的回波个数和弛豫分量个数,i=1,2,…,m;j=1,2,…,n;ti为采集时间(通常是回波间隔(Te)的整数倍];gi为测量得到的回波幅度;T2,j为预先选择的弛豫时间分布;μi为测量的误差;f(T2,i)为第i个弛豫分量对总的横向弛豫信号的贡献。展开式(1)可以得到方程组
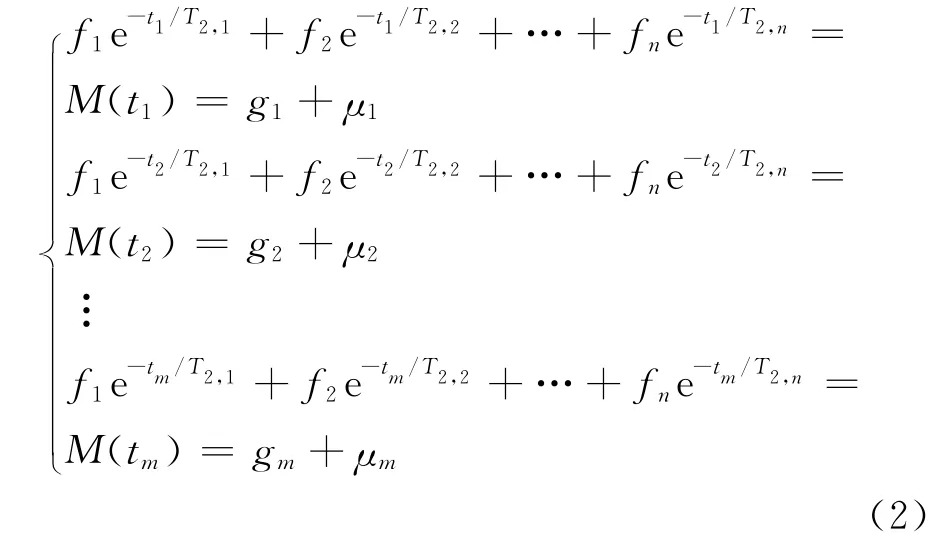
把式(2)写成向量的形式为

令

1.2 矩阵奇异值分解与方程组的解
在式(4)左右两边同乘A+得

根据矩阵的奇异值分解定理[7],对任意m×n阶矩阵A,存在m阶列正交矩阵U和n阶正交矩阵V,满足
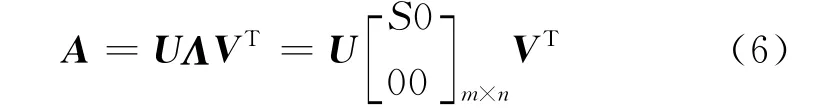
把式(7)代入式(5)可得

1.3 奇异值分解反演算法的改进
通常情况下,由式(8)解出的fi数值不稳定且会有负值出现,而fi的物理意义为第i种弛豫分量在0时刻的初始幅度值,是非负值。本文采取对系数矩阵加阻尼项的处理方法使其数值解稳定,应用迭代法对解进行非负性约束。
1.3.1 阻尼方法
根据式(4)建立式(10)目标函数求其极小值

可得
所以
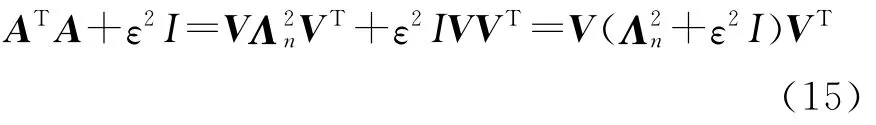
对式(15)求逆
把式(6)、式(16)代入式(13)可得

1.3.2 解的非负性约束
(1)置初始值fk,k=0;(k代表进行第k次迭代计算)
(2)dk⇐Afk;Δdk⇐d-dk;

(4)计算fk+1⇐fk+Δfk;
(5)如果(fk+1中的分量全部≥0)停机,输出fk+1,否则进行下一步;
(6)置fk+1中的负值为0,k=k+1转入第2步再次迭代,直到解满足非负约束条件为止。
2 反演实例及效果分析
2.1 无噪声理论数据反演及效果检验
为了检验该方法的解谱效果,构造T2谱,按方程(1)正演模型生成了无噪声理论回波串衰减曲线(见图1)。反演结果和构造的T2谱对比(见图2、图3)。可以看出,奇异截止值为10-6和奇异截止值为10-7反演的T2谱几乎完全一致,与构造的T2谱几乎完全吻合。这表明,SVD法可以准确地反演出真实的T2谱,奇异截止值对解谱效果影响小。
正演和反演的参数T2范围为(1×10-3)~3s,按对数分别布11个和30个T2点;1 000个回波串;回波间隔为0.6×10-3s。
2.2 不同信噪比数据反演及效果检验
给图1回波串信号分别加入信噪比SNR=5、25、50、100的高斯白噪声,其中加入SNR=5高斯白噪声后的回波曲线见图4。图5给出不同SNR数据反演结果与构造T2谱的对比。从图5可以看出,信噪比SNR=25、50、100的情况下,解谱结果与构造谱吻合得很好;信噪比SNR=5的情况下反演的T2谱和构造谱分布趋势一致,谱线光滑连续,大组分反演效果好,但小组分反演结果与构造谱相差较大,分辨率低;信噪比越高,反演所得的T2谱与构造谱的符合率越高。这表明,该方法反演高信噪比数据效果显著,而对低信噪比数据的反演可以保持波形特点大体一致。

图1 由构造谱生成的无噪声理论回波串衰减曲线
图2 11个布点反演无噪回波数据T2谱与构造谱对比图

图3 30个布点反演无噪回波数据T2谱与构造谱对比图
图4 由构造谱生成的信噪比SNR=5的理论回波曲线

表1 古89-47井岩心NMR实验参数表

表2 古89-47井岩心SVD解谱反演参数表
2.3 实验室NMR数据反演及效果检验
用该方法处理了大庆油田古89-47井1块岩心实验室NMR数据,解谱结果与实验室解谱结果对比见图6。岩心NMR实验参数和SVD解谱反演参数如表1和表2。

图5 不同信噪比理论回波数据反演T2谱与构造T2谱对比图
图6 古89-47井岩心SVD解谱与实验室解谱结果对比图
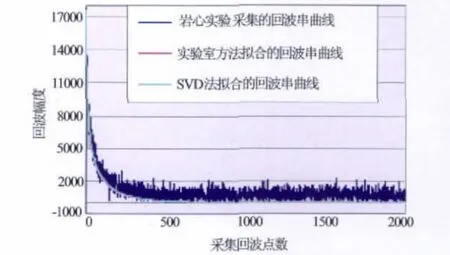
图7 古89-47井岩心测量的回波曲线及回波串的拟合曲线
从图6可以看出,岩心SVD法反演结果与实验室反演结果吻合得很好,谱的形状和变化趋势一致。从图7可以看出,SVD法多指数拟合曲线较好地拟合了岩心实验室采集的回波串曲线和实验室方法拟合的回波串曲线。上述结果表明改进的SVD法可以快速、有效地反演核磁共振T2谱,对提高核磁共振测井精细解释符合率有重要意义。
3 结 论
经过改进,SVD法可以有效反演出真实的T2谱,加阻尼项可以使数值解稳定。在布点数为11~128、信噪比大于25的情况下拟合精度较高,适用于高信噪比回波数据的反演,并且信噪比越高,反演的T2谱与构造谱的符合率越高。大组分比小组分反演分辨率高。同时新方法采用迭代的思想进行谱的非负性限制,而未删减原始测量数据,保证了T2谱的真实性和连续性。核磁共振实验室数据反演结果表明,该方法可以应用于实验室岩心T2谱反演。
[1] 肖立志.核磁共振成像测井与岩石核磁共振及其应用[M].北京:科学出版社,1998:11-18.
[2] Butler J P,Reeds J A,Dawson S V.Estimating Solutions of First Kind Integral Equations with Nonnegative Constraints and Optimal Smoothing[J].SIAMJ Numer Anal,1981,18(3):381-397.
[3] Dunn K J,Latorraca G A,Warner J L.On the Calculation and Interpretation of NMR Relaxation Time Distribution[C]∥SPE28367,69th Annual SPE Technical Conference and Exhibition,New Orleans,1994:45-54.
[4] 王忠东,肖立志,刘堂宴.核磁共振弛豫信号多指数反演新方法及其应用[J].中国科学:G辑,2003,33(4):323-333.
[5] Mohnke O,Yaramanci U.Smooth and Block Inversion of Surface NMR Amplitudes and Decay Times Usingsimulated Annealing[J].Journal of Applied Geophysics,2002,50:163-177.
[6] Dunn K J,Latorraca G A.The Inversion of NMR Log Data Sets with Different Measurement Errors[J].Journal of Magnetic Resonance,1999,140:153-161.
[7] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004:341-398.
